Wallis's conical edge
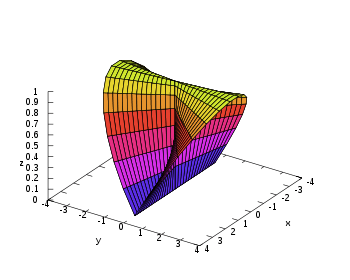
Figure 1. Wallis's Conical Edge with a=b=c=1
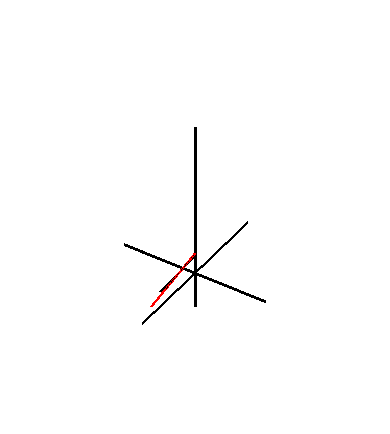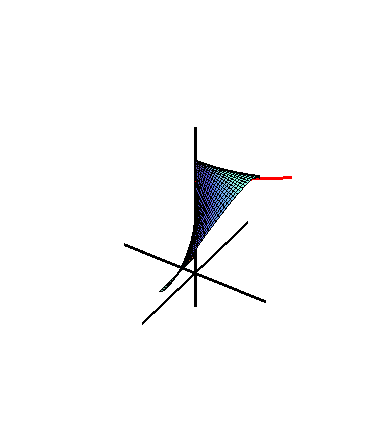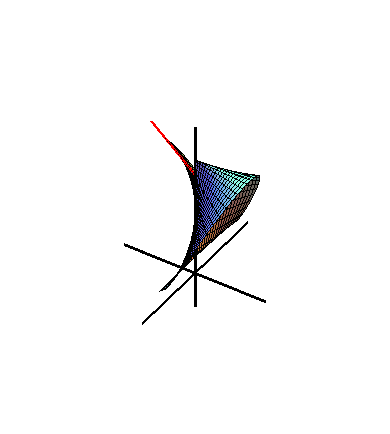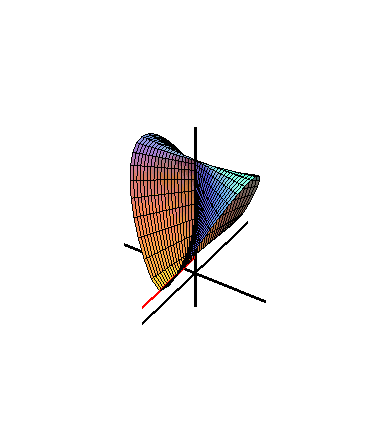
Figure 2. Wallis's Conical Edge with a=1.01,b=c=1
Wallis's conical edge is a ruled surface given by the parametric equations:
where a, b and c are constants.
Wallis's conical edge is also a kind of right conoid.
Figure 2 shows that the Wallis's conical edge is generated by a moving line.
Wallis's conical edge is named after the English mathematician John Wallis, who was one of the first to use Cartesian methods to study conic sections.
See also
External links
- Wallis's Conical Edge from MathWorld.
References
A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, FL:CRC Press, 2006. (ISBN 978-1-58488-448-4)
This article is issued from
Wikipedia.
The text is licensed under Creative Commons - Attribution - Sharealike.
Additional terms may apply for the media files.