Waffle-iron filter

A waffle-iron filter is a type of waveguide filter used at microwave frequencies for signal filtering. It is a variation of the corrugated-waveguide filter but with longitudinal slots cut through the corrugations resulting in an internal structure that has the appearance of a waffle-iron.
Waffle-iron filters are particularly suitable where both a wide passband, and a wide stopband free of spurious transmission modes, are required. They also have a high power-handling capability. Applications include suppressing the harmonic output of transmitters and the design of wide-band diplexers. They are also used in industrial microwave manufacturing processes to prevent the escape of microwave radiation from the microwave chamber. Filters with an analogous design are now appearing in photonics, but, due to the higher frequency, at a much smaller scale. This small size allows them to be incorporated into integrated circuits.
Design techniques for waffle-iron filters include image-parameter methods, network synthesis methods and numerical analysis methods. Network synthesis is a more advanced method than image-parameter techniques but the latter can still be used where a simple repeated-pattern design is desired. Numerical methods can be used to analyse either design.
Description
The waffle-iron filter was invented by Seymour B. Cohn at Stanford Research Institute in 1957.[1] The basis for the filter is the corrugated-waveguide filter. This consists of a series of ridges, or corrugations, across the width of the filter. There are corrugations inside the waveguide on both the top and bottom surfaces. The rising and descending ridges are aligned with each other but do not meet in the middle; there is a gap in between. In the waffle-iron filter there are, in addition, slots cut through the ridges down the length of the waveguide. This leaves a matrix of square islands, or teeth, on the top and bottom surfaces.[2]
Waffle-iron filters are, in essence, low-pass filters but like all waveguide devices will not transmit anything below the waveguide cutoff frequency. Waffle-iron filters are used where both a wide passband with low insertion loss, and a wide (sometimes very wide) stopband are needed. They are particularly good where suppression of spurious modes is required.[3]
Waffle-iron filters have been built with a 10 GHz wide stopband and 60 dB attenuation.[4] Even wider stopbands are possible with a relaxed attenuation specification.[5]
Operation
One of the performance issues addressed by the waffle-iron filter is that in many waveguide filters the attenuation is dependent on the transmission modes of the incident signal and some filters can be quite bad at suppressing spurious modes which may be contained in this signal. For instance, with the corrugated waveguide filter, on which the waffle-iron filter is based, attenuation of TEn0 modes in the stopband is strongly dependent on the mode number. This is not the case with the waffle-iron filter which attenuates all TEn0 modes nearly equally up to a certain frequency. The limit is the frequency at which the distance between the metal teeth is greater than half the free-space wavelength of the signal. The reason for the waffle-iron design's good performance in this respect is that the distance between the teeth is the same in both the longitudinal and transverse directions and nearly the same in all directions in between. This makes the waffle-iron nearly isotropic to TEM waves in all these directions. Since any TEn0 mode wave can be decomposed into two TEM mode waves travelling in different diagonal directions, all TEn0 modes are affected nearly equally.[6]
Incident signals containing TM modes above a certain frequency can generate modes which propagate along the longitudinal slots with the slots themselves acting as waveguides. The point at which this can start to happen is the frequency at which the height of the slot is greater than half the free-space wavelength of the signal. If this frequency is above the required stopband of the filter the effect is of no consequence. Otherwise, steps outside the filter are needed to suppress these modes and can be incorporated into the end-matching sections.[7]
Other design criteria will usually result in a filter which does not match the waveguides to which it is to be connected at its input and output. There are many structures that can be used for matching but a useful one here is the stepped-impedance transformer which has the added advantage of helping to suppress the unwanted slot modes.[8]
Applications
A common application of waffle-iron filters is to remove the harmonics of transmitters, such as high power radar, before applying to the antenna. Legislation in most jurisdictions requires strict limits on out-of-band transmissions since these can cause serious interference with other stations. This is an application that usually requires a very wide stopband, a characteristic of waffle-iron filters. For instance, to remove all harmonics up to the fifth it is necessary for a low-pass filter to have a stopband greater than three times the passband.[9]
The wide-band nature of waffle-iron filters finds applications in satellite communications. A satellite earth station may have multiple diplexers connected to a multi-band antenna feeder. Each diplexer delivers a wide-band signal in a different band and it is essential that its signal does not contain out-of-band components, particularly harmonics. These can seriously interfere with, or even stop entirely, communication in another band. The diplexer must therefore have a stopband that is even wider than the passband. For this reason, as well as the other advantages of waffle-irons, these diplexers are commonly made to a waffle-iron design.[10]
Waffle-iron filters are used in industrial microwave processes. The many industrial applications of microwave energy include drying of food products and industrial films, heating, such as in polyurethane foam production, melting, rendering, sterilising, and vulcanisation. In high-volume production the process is continuous necessitating openings to the microwave chamber where the product can be fed in and exit. Steps need to be taken to prevent unsafe levels of microwave radiation escaping from these apertures which are often large to accommodate the product. It is usual to line the product feed ducts with microwave absorbent material for this purpose. However, the absorbed microwaves have a heating effect and this can be severe enough to damage the absorbent material. Waffle-iron filters are a useful alternative because the product can be passed between the filter's teeth. An ideal filter will reflect all the unwanted radiation rather than absorbing it so will not suffer from overheating. This is an example of a filter being used in a choke application. In some processes both techniques are used simultaneously. The waffle-iron is placed nearest the microwave chamber to first reduce the energy to a level which will not cause the absorbent lining to overheat. The absorbent lining then removes the small residue.[11]
Design
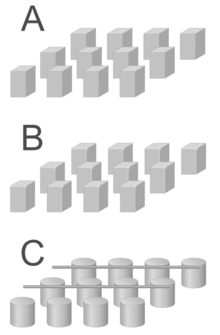
The number of teeth, their size, and the gap between them are all design parameters that can be used to control the design of the filter. As an example, a filter with a 3:1 stopband might have five teeth across the width of the waveguide. The number of rows of teeth down the length of the waveguide primarily affects the stopband attenuation. The more rows of teeth, the better the attenuation, each row being equivalent to a lumped element circuit filter section. A filter with ten rows of teeth has a theoretical stopband rejection of around 80 dB and one with seven rows around 60 dB.[12]
The earliest waffle-iron filters were designed with the image parameter method of filter design. Cohn's original data for the corrugated filter could also be applied to the waffle-iron with only a small adjustment of one parameter. An alternative approach to using Cohn's empirical data, but still an image parameter design, is due to Marcuvitz who used a waveguide T-junction equivalent circuit to represent corrugations and this method was later extended by others to waffle-irons.[13]
One of the main drawbacks of the image parameter design method in this, as in other, filters is that the impedance match at the terminations is not good. This usually requires that impedance matching sections are provided at the input and output. These usually take the form of multi-section stepped impedance transformers. These add considerably to the overall length of the filter.[14] A small improvement to matching can be had by starting and ending the filter on a half-space instead of a full tooth or space. The lumped circuit equivalent of this is T-half-sections terminating the filter at either end. Starting and ending on a half-tooth instead of a half space is the equivalent of Π-half-sections.[15]
Direct synthesis avoids many of the problems of the image parameter method. Not only does it take better account of the terminal impedances but the designer has additional degrees of freedom allowing improved matching. The size and gaps of the teeth are tapered in this method of design. That is, the teeth can be different sizes according to their position in the filter, compared with an image design where all sections are identical. With this approach, the original specification for passband and stopband can be kept while simultaneously improving the impedance matching. The stepped impedance transformers can be dispensed with, or at least significantly reduced in size.[16]
Synthesis methods allow better control of the precise filter response. A common response function used by filter designers is the Chebyshev filter which trades steepness of the transition band for passband ripple. However the Chebyshev response is not always the best choice for waffle-iron filters. Low-pass waveguide filters do not pass frequencies all the way down to zero because of the waveguide cutoff effect. A better choice is the Achieser-Zolotarev filter. This filter is based on Zolotarev polynomials (which include the Chebyshev polynomials as a special case) discovered by Yegor Ivanovich Zolotarev. The Zolotarev response has a stopband at low frequency, the cutoff of which can be controlled by the designer so it is not detrimental in a waveguide filter. The advantage of the Zolotarev response is that it results in a filter with a better impedance match to the connecting waveguides compared to the Chebyshev filter or image-parameter filters.[17]
Another design approach, particularly suitable for CAD because it is a numerical method, is to decompose the filter into a number of finite elements. These elements are a large number of simple steps and ridges. A number of methods are available to analyse the individual elements. The mode matching technique expands the field equations of the element into a series of eigenfunctions and then for each mode matches the field at the interface between elements.[18] The Galerkin method expands the field equations into polynomial functions such as Gegenbauer polynomials or Chebyshev polynomials. These methods can be mixed according to what is convenient for a particular type of element. Whichever analysis method is used, the final output needed is the scattering parameters matrix for each element. The overall filter response is then found from the combined scattering matrix of all the individual element matrices. This method is analytic rather than synthetic, that is, a trial design must first exist in order to be analysed unlike synthesis methods where the starting point is a prescribed transfer function from which a design is synthesised.[19]
TE0n modes should not, in theory, be excited in the waffle-iron filter because of its vertical symmetry about the centre-line. However, in practice they can be caused by poorly mating waveguide flanges or misaligned teeth. These spurious modes can be suppressed by fitting thin wires across the width of the filter in the space between the teeth on the vertical centre-line of the waveguide. This can be a better solution than over-engineering the components to high precision and results in a more robust design.[20]
Multiple unit filters
Very wide stopbands can be achieved by cascading several waffle-iron filter units together. Each unit is designed for a stopband in different, but overlapping, ranges. The filter with the highest frequency stopband has the smallest, and greatest number, of teeth. The units are connected together with λ/4 impedance transformer sections of waveguide in order of progressively higher frequency operation. Since the impedance transformers are operating at different frequencies the ones connected to the units with smallest teeth are shorter than those connected to units with larger teeth. Matthaei gives an example of a three unit waffle-iron filter designed to stop all harmonics of the passband from the second to the tenth – a combined stopband of 2.2 GHz to 13.7 GHz with a rejection of 60 dB.[21]
Using network synthesis design techniques the need for multiple units can be reduced or eliminated. If tapering of the teeth is allowed, a two-unit design can often be reduced to a single unit with the same wide stopband. This approach can halve the length of the complete filter.[22]
High power
At high power, arcing can occur at the corners of the filter teeth due to strong electric fields being present at sharp corners. This limits the power-handling capability of the filter. The effect can be mitigated by rounding the edges of the teeth. Completely circular teeth are best of all for power handling. Circular teeth will handle about 1.4 times the power capability of square teeth without arcing. For instance Matthaei describes a 1.2–1.64 GHz passband filter with rounded teeth and a wide stopband with a power-handling capability of 1.4 MW. A similar filter with circular teeth, on the other hand, can handle 2 MW. Using power dividers to connect filters in parallel and then combining their outputs can provide even greater power handling.[23]
Photonics
Filter structures that are analogous to the waffle-iron filter are used in photonics but operate at a much higher frequency and are much smaller than those used in electronics. Like the waffle-iron, these structures have good suppression of unwanted transmission modes. A filter operating in the 0.1 to 4.0 THz band has been built using parallel-plate waveguide (PPWG[24]) technology with 50 dB of rejection in the stopband. The filter was constructed of two plates of highly polished aluminium spaced 100 μm apart. The teeth consisted of gold-sputtered aluminium cylinders on a silicon die. In this design it is not convenient to provide a gap through the centre of the teeth as is done in the microwave version. Instead, the air gap is provided between the top of the teeth and one of the PPWG plates.[25]
These filters can be made using the standard semiconductor industry photolithography manufacturing techniques. Consequently, they are suitable for incorporating into on-chip integrated circuits, as is PPWG technology in general.[26]
References
- ↑ Young, p.10
- ↑ Matthaei et al., p.390
- ↑ Levy, pp.526, 527
Manuilov and Kobrin, 2005, p.93
Manuilov et al., 2009, p.526
Matthaei et al., p.390 - ↑ Bingham, p.29
- ↑ Matthaei et al., p.393
- ↑ Matthaei et al., pp.390–391
- ↑ Matthaei et al., pp.391–392
- ↑ Matthaei et al., pp.392–393
- ↑ Gerke and Kimmel, pp.7–8
Levy, p.526
Mendenhall, pp.805–806 - ↑ Manuilov and Kobrin, 2005, p.93
Manuilov et al., 2009, p.526 - ↑ Mehdizadeh, pp.329–331
Metaxas and Meredith, pp.301–303 - ↑ Matthaei et al., pp.392, 938
- ↑ Cohn, pp.651–656
Marcuvitz, pp.336–350
Matthaei et al., p.392 - ↑ Levy, p.526
Matthaei et al., pp.397–408 - ↑ Matthaei et al., pp.393, 404–408
- ↑ Levy, p.1
- ↑ Levy, pp.528–530
- ↑ Van Riemen, p.36
- ↑ Arndt et al., p.186
Manuilov and Kobrin, 2005, pp.93–94
Manuilov et al., 2009, pp.527–528 - ↑ Matthaei et al., pp.951–952
- ↑ Matthaei et al., pp.938–941
Sharp, p.111 - ↑ Levy p.530
- ↑ Matthaei et al., pp.393, 408–409, 938–947
- ↑ Avetisyan et al., p.327
- ↑ Bingham, pp.10–31
- ↑ Bingham pp.5–6, 17–18
Avetisyan et al., p.331
Bibliography
- Arndt, F.; Beyer, R.; Hauth, W.; Schmitt, D.; Zeh, H., "Cascaded wide stop band waffle-iron filter designed with a MM/FE CAD method", 29th European Microwave Conference, 1999, pp. 186–189.
- Avetisyan, Yu.H.; Manukyan, A.H.; Hakobyan, H.S.; Poghosyan, T.N., "Two-Dimensional confined Terahertz wave propagation in gap plasmon waveguide formed by two cylindrical surfaces", Modern Optics and Photonics: Atoms and Structured Media, pp. 325–338, World Scientific, 2010 ISBN 981-4313-26-2.
- Bingham, Adam L., Propagation Through Terahertz Waveguides with Photonic Crystal Boundaries, ProQuest, 2007 ISBN 0-549-51329-9.
- Cohn, Seymour B., "Analysis of a wide-band waveguide filter", Proceedings of the IRE, vol.37, iss.6, pp. 651–656, June 1949.
- Gerke, Daryl; Kimmel, Bill, EDN Designers Guide to Electromagnetic Compatibility, Newnes, 2002 ISBN 0-7506-7654-X.
- Gurzadyan, Gagik G.; Kryuchkyan, Gagik Yu; Papoyan, Aram V., Modern Optics and Photonics: Atoms and Structured Media, World Scientific, 2010 ISBN 981-4313-26-2.
- Levy, Ralph, "Tapered corrugated waveguide low-pass filters", IEEE Transactions on Microwave Theory and Techniques, vol.21, iss.8, pp. 526–532, August 1973.
- Manuilov, Mikhail B.; Kobrin, Konstantin V., "Low-loss waffle-iron filters for multiband feeders of reflector antennas", Proceedings of International Symposium on Antennas and Propagation (ISAP2005), pp. 93–96, Seoul: Korea Electromagnetic Engineering Society, 2005 ISBN 89-86522-77-2.
- Manuilov, M. B.; Kobrin, K. V.; Sinyavsky, G. P.; Labunko, O. S., "Full wave hybrid technique for CAD of passive waveguide components with complex cross section", PIERS Online, vol.5, no.6, pp. 526–530, 2009.
- Marcuvitz, Nathan, Waveguide Handbook, New York: McGraw Hill, 1951 OCLC 680485.
- Matthaei, George L.; Young, Leo; Jones, E. M. T., Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964 OCLC 299575271
- Mehdizadeh, Mehrdad, Microwave/RF Applicators and Probes for Material Heating, Sensing, and Plasma Generation, Oxford: William Andrew, 2009 ISBN 0-8155-1592-8.
- Mendenhall, Geoffrey N., "FM and digital radio broadcast transmitters", Engineering Handbook, pp. 777–823, Burlington MA: Focal Press, 2007 ISBN 0-240-80751-0.
- Metaxas, A. C.; Meredith, Roger J., Industrial Microwave Heating, Stevenage: Peter Peregrinus, 1993 ISBN 0-906048-89-3.
- Sharp, E.D., "A high-power wide-band waffle-iron filter", IEEE Transactions on Microwave Theory and Techniques, vol.11, iss.2, pp. 111–116, March 1963.
- Van Rienen, Ursula, Numerical Methods in Computational Electrodynamics Springer, 2001 ISBN 3-540-67629-5.
- Young, Leo, "Microwave filters", IEEE Transactions on Circuit Theory, vol.11, iss.1, pp. 10–12, March 1964.