Triangular prismatic honeycomb
| Triangular prismatic honeycomb | |
|---|---|
 | |
| Type | Uniform honeycomb |
| Schläfli symbol | {3,6}×{∞} or t0,3{3,6,2,∞} |
| Coxeter diagrams | |
| Space group Coxeter notation | [6,3,2,∞] [3[3],2,∞] [(3[3])+,2,∞] |
| Dual | Hexagonal prismatic honeycomb |
| Properties | vertex-transitive |
The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed entirely of triangular prisms.
It is constructed from a triangular tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Related honeycombs
Hexagonal prismatic honeycomb
| Hexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbols | {6,3}×{∞} or t0,1,3{6,3,2,∞} |
| Coxeter diagrams |
|
| Cell types | 4.4.6 |
| Vertex figure | triangular bipyramid |
| Space group Coxeter notation | [6,3,2,∞] [3[3],2,∞] |
| Dual | Triangular prismatic honeycomb |
| Properties | vertex-transitive |
The hexagonal prismatic honeycomb or hexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of hexagonal prisms.
It is constructed from a hexagonal tiling extruded into prisms.

It is one of 28 convex uniform honeycombs.
This honeycomb can be alternated into the gyrated tetrahedral-octahedral honeycomb, with pairs of tetrahedra existing in the alternated gaps (instead of a triangular bipyramid).
Trihexagonal prismatic honeycomb
| Trihexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | r{6,3}x{∞} or t1,3{6,3}x{∞} |
| Vertex figure | Rectangular bipyramid |
| Coxeter diagram | |
| Space group Coxeter notation | [6,3,2,∞] |
| Dual | Rhombille prismatic honeycomb |
| Properties | vertex-transitive |
The trihexagonal prismatic honeycomb or trihexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of hexagonal prisms and triangular prisms in a ratio of 1:2.

It is constructed from a trihexagonal tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Truncated hexagonal prismatic honeycomb
| Truncated hexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | t{6,3}×{∞} or t0,1,3{6,3,2,∞} |
| Coxeter diagram | |
| Cell types | 4.4.12 3.4.4 |
| Face types | {3}, {4}, {12} |
| Edge figures | Square, Isosceles triangle |
| Vertex figure | Triangular bipyramid |
| Space group Coxeter notation | [6,3,2,∞] |
| Dual | Triakis triangular prismatic honeycomb |
| Properties | vertex-transitive |
The truncated hexagonal prismatic honeycomb or tomo-trihexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of dodecagonal prisms, and triangular prisms in a ratio of 1:2.

It is constructed from a truncated hexagonal tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Rhombitrihexagonal prismatic honeycomb
| Rhombitrihexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Vertex figure | Trapezoidal bipyramid |
| Schläfli symbol | rr{6,3}×{∞} or t0,2,3{6,3,2,∞} s2{3,6}×{∞} |
| Coxeter diagram | |
| Space group Coxeter notation | [6,3,2,∞] |
| Dual | Deltoidal trihexagonal prismatic honeycomb |
| Properties | vertex-transitive |
The rhombitrihexagonal prismatic honeycomb or rhombitrihexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of hexagonal prisms, cubes, and triangular prisms in a ratio of 1:3:2.

It is constructed from a rhombitrihexagonal tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Snub hexagonal prismatic honeycomb
| Snub hexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | sr{6,3}×{∞} |
| Coxeter diagram | |
| Symmetry | [(6,3)+,2,∞] |
| Dual | Floret pentagonal prismatic honeycomb |
| Properties | vertex-transitive |
The snub hexagonal prismatic honeycomb or simo-trihexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of hexagonal prisms and triangular prisms in a ratio of 1:8.

It is constructed from a snub hexagonal tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Truncated trihexagonal prismatic honeycomb
| Truncated trihexagonal prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | tr{6,3}×{∞} or t0,1,2,3{6,3,2,∞} |
| Coxeter diagram | |
| Space group Coxeter notation | [6,3,2,∞] |
| Vertex figure | irr. triangular bipyramid |
| Dual | Kisrhombille prismatic honeycomb |
| Properties | vertex-transitive |
The truncated trihexagonal prismatic honeycomb or tomo-trihexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of dodecagonal prisms, hexagonal prisms, and cubes in a ratio of 1:2:3.

It is constructed from a truncated trihexagonal tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Elongated triangular prismatic honeycomb
| Elongated triangular prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbols | {3,6}:e×{∞} s{∞}h1{∞}×{∞} |
| Coxeter diagrams | |
| Space group Coxeter notation | [∞,2+,∞,2,∞] [(∞,2)+,∞,2,∞] |
| Dual | Prismatic pentagonal prismatic honeycomb |
| Properties | vertex-transitive |
The elongated triangular prismatic honeycomb or elongated antiprismatic prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.

It is constructed from an elongated triangular tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Gyrated triangular prismatic honeycomb
| Gyrated triangular prismatic honeycomb | |
|---|---|
| Type | Convex uniform honeycomb |
| Schläfli symbols | {3,6}:g×{∞} {4,4}f{∞} |
| Cell types | (3.4.4) |
| Face types | {3}, {4} |
| Vertex figure |  |
| Space group | [4,(4,2+,∞,2+)] ? |
| Dual | ? |
| Properties | vertex-transitive |
The gyrated triangular prismatic honeycomb or parasquare fastigial cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of triangular prisms. It is vertex-uniform with 12 triangular prisms per vertex.


It can be seen as parallel planes of square tiling with alternating offsets caused by layers of paired triangular prisms. The prisms in each layer are rotated by a right angle to those in the next layer.
It is one of 28 convex uniform honeycombs.
Pairs of triangular prisms can be combined to create gyrobifastigium cells. The resulting honeycomb is closely related but not equivalent: it has the same vertices and edges, but different two-dimensional faces and three-dimensional cells.
Gyroelongated triangular prismatic honeycomb
| Gyroelongated triangular prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbols | {3,6}:ge×{∞} {4,4}f1{∞} |
| Vertex figure | 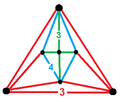 |
| Space group Coxeter notation | [4,(4,2+,∞,2+)] ? |
| Dual | - |
| Properties | vertex-transitive |
The gyroelongated triangular prismatic honeycomb or elongated parasquare fastigial cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.


It is created by alternating laters of cubes and triangular prisms, with the prisms alternating in orientation by 90 degrees.
It is related to the elongated triangular prismatic honeycomb which has the triangular prisms with the same orientation.
This is related to a space-filling polyhedron, elongated gyrobifastigium, where cube and two opposite triangular prisms are augmented together as a single polyhedron:
See also
References
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- Klitzing, Richard. "3D Euclidean Honeycombs tiph".
- Uniform Honeycombs in 3-Space VRML models
