Transversal (geometry)

In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two other lines in the Euclidean plane are parallel. The intersections of a transversal with two lines create various types of pairs of angles: consecutive interior angles, corresponding angles, and alternate angles. By Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equal.

   
Eight angles of a transversal.
(Vertical angles such as and

are always congruent.)

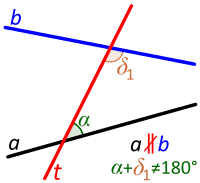
   Transversal between non-parallel lines.
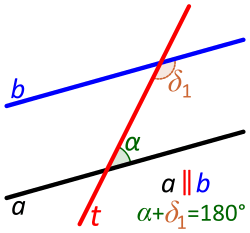
Consecutive angles are not supplementary.		 Transversal between parallel lines.
Consecutive angles are supplementary.

Angles of a transversal

A transversal produces 8 angles, as shown in the graph at the above left:

A transversal that cuts two parallel lines at right angles is called a perpendicular transversal. In this case, all 8 angles are right angles [1]

When the lines are parallel, a case that is often considered, a transversal produces several congruent and several supplementary angles. Some of these angle pairs have specific names and are discussed below:[2][3]corresponding angles, alternate angles, and consecutive angles.

Corresponding angles

One pair of corresponding angles. With parallel lines, they are congruent.

Corresponding angles are the four pairs of angles that:

Two lines are parallel if and only if the two angles of any pair of corresponding angles of any transversal are congruent (equal in measure).

Note: This follows directly from Euclid's parallel postulate. Further, if the angles of one pair are congruent, then the angles of each of the other pairs are also congruent. In our images with parallel lines, corresponding angle pairs are: α=α1, β=β1, γ=γ1 and δ=δ1.

Alternate angles

One pair of alternate angles. With parallel lines, they are congruent.

Alternate angles are the four pairs of angles that:

If the two angles of one pair are congruent (equal in measure), then the angles of each of the other pairs are also congruent.

Proposition 1.27 of Euclid's elements, a theorem of absolute geometry (hence valid in both hyperbolic geometry and Euclidean Geometry), proves that if the angles of a pair of alternate angles of a transversal are congruent then the two lines are parallel (non-intersecting) .

It follows from Euclid's parallel postulate that if the two lines are parallel, then the angles of a pair of alternate angles of a transversal are congruent (Proposition 1.29 of Euclid's elements).

Consecutive interior angles

One pair of consecutive angles. With parallel lines, they add up to two right angles

Consecutive interior angles are the two pairs of angles that:[4][2]

Two lines are parallel if and only if the two angles of any pair of consecutive interior angles of any transversal are supplementary (sum to 180°).

By the definition of a straight line and the properties of vertical angles, if one pair is supplementary, the other pair is also supplementary.

Other characteristics of transversals

If three lines in general position form a triangle are then cut by a transversal, the lengths of the six resulting segments satisfy Menelaus' theorem.

Euclid's formulation of the parallel postulate may be stated in terms of a transversal. Specifically, if the interior angles on the same side of the transversal are less than two right angles then lines must intersect. In fact, Euclid uses the same phrase in Greek that is usually translated as "transversal".[5]

Euclid's Proposition 27 states that if a transversal intersects two lines so that alternate interior angles are congruent, then the lines are parallel. Euclid proves this by contradiction: If the lines are not parallel then they must intersect and a triangle is formed. Then one of the alternate angles is an exterior angle equal to the other angle which is an opposite interior angle in the triangle. This contradicts Proposition 16 which states that an exterior angle of a triangle is always greater than the opposite interior angles.[6][7]

Euclid's Proposition 28 extends this result in two ways. First, if a transversal intersects two lines so that corresponding angles are congruent, then the lines are parallel. Second, if a transversal intersects two lines so that interior angles on the same side of the transversal are supplementary, then the lines are parallel. These follow from the previous proposition by applying the fact that opposite angles of intersecting lines are equal (Prop. 15) and that adjacent angles on a line are supplementary (Prop. 13). As noted by Proclus, Euclid gives only three of a possible six such criteria for parallel lines.[8][9]

Euclid's Proposition 29 is a converse to the previous two. First, if a transversal intersects two parallel lines, then the alternate interior angles are congruent. If not, then one is greater than the other, which implies its supplement is less than the supplement of the other angle. This implies that there are interior angles on the same side of the transversal which are less than two right angles, contradicting the fifth postulate. The proposition continues by stating that on a transversal of two parallel lines, corresponding angles are congruent and the interior angles on the same side are equal to two right angles. These statements follow in the same way that Prop. 28 follows from Prop. 27.[10][11]

Euclid's proof makes essential use of the fifth postulate, however, modern treatments of geometry use Playfair's axiom instead. To prove proposition 29 assuming Playfair's axiom, let a transversal cross two parallel lines and suppose that the alternate interior angles are not equal. Draw a third line through the point where the transversal crosses the first line, but with an angle equal to the angle the transversal makes with the second line. This produces two different lines through a point, both parallel to another line, contradicting the axiom.[12][13]

References

  1. ↑ "Transversal". Math Open Reference. 2009. (interactive)
  2. 1 2 Rod Pierce (2011). "Parallel Lines". MathisFun. (interactive)
  3. ↑ Holgate Art. 87
  4. ↑ C.Clapham, J.Nicholson (2009). "Oxford Concise Dictionary of Mathematics" (PDF). Addison-Wesley. p. 582.
  5. ↑ Heath p. 308 note 1
  6. ↑ Heath p. 307
  7. ↑ See also Holgate Art. 88
  8. ↑ Heath p. 309-310
  9. ↑ See also Holgate Art. 89-90
  10. ↑ Heath p. 311-312
  11. ↑ See also Holgate Art. 93-95
  12. ↑ Heath p. 313
  13. ↑ A similar proof is given in Holgate Art. 93
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.