Tangent-secant theorem

\triangle PTG_{2}\sim \triangle PG_{1}T

\Rightarrow

{\frac {|PT|}{|PG_{2}|}}={\frac {|PG_{1}|}{|PT|}}

\Rightarrow

|PT|^{2}=|PG_{1}|\cdot |PG_{2}|

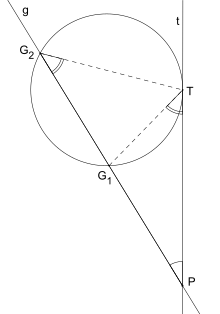
The tangent-secant theorem describes the relation of line segments created by a secant and a tangent line with the associated circle.

For a secant g intersecting the circle in G₁ and G₂ and tangent t intersecting the circle in T that intersect in P the following equation holds:

|PT|^{2}=|PG_{1}|\cdot |PG_{2}|

The tangent secant theorem can be proven using similar triangles (see graphic). Next to the intersecting chords theorem and the intersecting secants theorem it represents one of the three basic cases of a more general theorem about two intersecting lines and a circle - the power of point theorem.

References

S. Gottwald: The VNR Concise Encyclopedia of Mathematics. Springer, 2012, ISBN 9789401169820, pp. 175-176
Michael L. O'Leary: Revolutions in Geometry. Wiley, 2010, ISBN 9780470591796, p. 161
Schülerduden - Mathematik I. Bibliographisches Institut & F.A. Brockhaus, 8. Auflage, Mannheim 2008, ISBN 978-3-411-04208-1, pp. 415-417 (German)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.