Symmetrization methods
In mathematics the symmetrization methods are algorithms of transforming a set to a ball with equal volume and centered at the origin. B is called the symmetrized version of A, usually denoted . These algorithms show up in solving the classical isoperimetric inequality problem, which asks: Given all two-dimensional shapes of a given area, which of them has the minimal perimeter (for details see Isoperimetric inequality). The conjectured answer was the disk and Steiner in 1838 showed this to be true using the Steiner symmetrization method (described below). From this many other isoperimetric problems sprung and other symmetrization algorithms. For example, Rayleigh's conjecture is that the first eigenvalue of the Dirichlet problem is minimized for the ball (see Rayleigh–Faber–Krahn inequality for details). Another problem is that the Newtonian capacity of a set A is minimized by and this was proved by Polya and G. Szego (1951) using circular symmetrization (described below).
Symmetrization
If is measurable, then it is denoted by the symmetrized version of i.e. a ball such that . We denote by the symmetric decreasing rearrangement of nonnegative measurable function f and define it as , where is the symmetrized version of preimage set . The methods described below have been proved to transform to i.e. given a sequence of symmetrization transformations there is , where is the Hausdorff distance (for discussion and proofs see Burchard (2009))
Steiner symmetrization
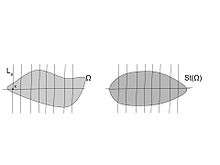
Steiner symmetrization was introduced by Steiner (1838) to solve the isoperimetric theorem stated above. Let be a hyperplane through the origin. Rotate space so that is the hyperplane. For each let the perpendicular line through be . Then by replacing each by a line centered at H and with length we obtain the Steiner symmetrized version.
It is denoted by the Steiner symmetrization wrt to hyperplane of nonnegative measurable function and for fixed define it as
Circular symmetrization
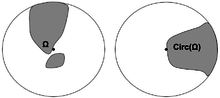
A popular method for symmetrization in the plane is Polya's circular symmetrization. After, its generalization will be described to higher dimensions. Let be a domain; then its circular symmetrization with regards to the positive real axis is defined as follows: Let
i.e. contain the arcs of radius t contained in . So it is defined
- If is the full circle, then .
- If the length is , then .
- iff .
In higher dimensions , its spherical symmetrization wrt to positive axis of is defined as follows: Let i.e. contain the caps of radius r contained in . Also, for the first coordinate let if . So as above
- If is the full cap, then .
- If the surface area is , then and where is picked so that its surface area is . In words, is a cap symmetric around the positive axis with the same area as the intersection .
- iff .
Polarization
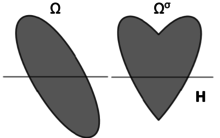
Let be a domain and be a hyperplane through the origin. Denote the reflection across that plane to the positive halfspace as or just when it is clear from the context. Also, the reflected across hyperplane H is defined as . Then, the polarized is denoted as and defined as follows
- If , then .
- If , then .
- If , then .
In words, is simply reflected to the halfspace . It turns out that this transformation can approximate the above ones (in the Hausdorff distance) (see Brock & Solynin (2000)).
References
- Morgan, Frank (2009). "Symmetrization". Retrieved November 2015. Check date values in:
|access-date=(help) - Burchard, Almut (2009). "A Short Course on Rearrangement Inequalities" (PDF). Retrieved November 2015. Check date values in:
|access-date=(help)
- Kojar, Tomas (2015). "Brownian Motion and Symmetrization". arXiv:1505.01868
 .
.
- Brock, Friedemann; Solynin, Alexander (2000), "An approach to symmetrization via polarization.", Transactions of the American Mathematical Society, 352: 1759–1796