Subpaving
In mathematics, a subpaving is a set of nonoverlapping box of Rn. A subset X of Rn can be approximated by two subpavings X− and X+ such that X− ⊂ X ⊂ X+. The three figures on the right show an approximation of the set X = {(x1, x2) ∈ R2 | x12 + x22 + sin(x1 + x2) ∈ [4,9]} with different accuracies. The set X− corresponds to red boxes and the set X+ contains all red and yellow boxes.


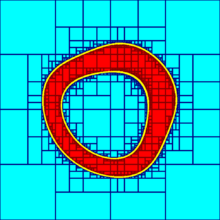
Combined with interval-based methods, subpavings are used to approximate the solution set of non-linear problems such as set inversion problems. [1] Subpavings can also be used to prove that a set defined by nonlinear inequalities is path connected [2] , to provide topological properties of such sets [3] , to solve piano-mover's problems [4] or to implement set computation [5] .
References
- ↑ Jaulin, Luc; Walter, Eric (1993). "Set inversion via interval analysis for nonlinear bounded-error estimation" (PDF). Automatica. 29 (4).
- ↑ Delanoue, N.; Jaulin, L.; Cottenceau, B. (2005). "Using interval arithmetic to prove that a set is path-connected" (PDF). Theoretical Computer Science, Special issue: Real Numbers and Computers. 351 (1).
- ↑ Delanoue, N.; Jaulin, L.; Cottenceau, B. (2006). "Counting the Number of Connected Components of a Set and Its Application to Robotics" (PDF). Applied Parallel Computing, Lecture Notes in Computer Science. 3732 (1).
- ↑ Jaulin, L. (2001). "Path planning using intervals and graphs" (PDF). Reliable Computing. 7 (1).
- ↑ Kieffer, M.; Jaulin, L.; Braems, I.; Walter, E. (2001). "Guaranteed set computation with subpavings" (PDF). In W. Kraemer and J. W. Gudenberg (Eds), Scientific Computing, Validated Numerics, Interval Methods, Kluwer Academic Publishers.