Steric 6-cubes
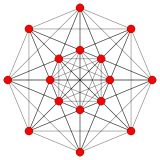 6-demicube |
 Steric 6-cube |
 Stericantic 6-cube |
 Steriruncic 6-cube |
 Stericruncicantic 6-cube | |
| Orthogonal projections in D6 Coxeter plane | ||
|---|---|---|
In six-dimensional geometry, a steric 6-cube is a convex uniform 6-polytope. There are unique 4 steric forms of the 6-cube.
Steric 6-cube
| Steric 6-cube | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t0,3{3,33,1} h4{4,34} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 3360 |
| Vertices | 480 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
Alternate names
- Runcinated demihexeract/6-demicube
- Small prismated hemihexeract (Acronym sophax) (Jonathan Bowers)[1]
Cartesian coordinates
The Cartesian coordinates for the 480 vertices of a steric 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±1,±3)
with an odd number of plus signs.
Images
| Coxeter plane | B6 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12/2] | |
| Coxeter plane | D6 | D5 |
| Graph |  |
 |
| Dihedral symmetry | [10] | [8] |
| Coxeter plane | D4 | D3 |
| Graph | 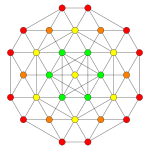 |
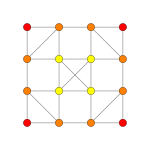 |
| Dihedral symmetry | [6] | [4] |
| Coxeter plane | A5 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
Related polytopes
| Dimensional family of steric n-cubes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 5 | 6 | 7 | 8 | |||||||
| [1+,4,3n-2] = [3,3n-3,1] |
[1+,4,33] = [3,32,1] |
[1+,4,34] = [3,33,1] |
[1+,4,35] = [3,34,1] |
[1+,4,36] = [3,35,1] | |||||||
| Steric figure |
 |
 |
 |
 | |||||||
| Coxeter | = |
= |
= |
= | |||||||
| Schläfli | h4{4,33} | h4{4,34} | h4{4,35} | h4{4,36} | |||||||
Stericantic 6-cube
| Stericantic 6-cube | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t0,1,3{3,33,1} h2,4{4,34} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 12960 |
| Vertices | 2880 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
Alternate names
- Runcitruncated demihexeract/6-demicube
- Prismatotruncated hemihexeract (Acronym pithax) (Jonathan Bowers)[2]
Cartesian coordinates
The Cartesian coordinates for the 2880 vertices of a stericantic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B6 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12/2] | |
| Coxeter plane | D6 | D5 |
| Graph |  |
 |
| Dihedral symmetry | [10] | [8] |
| Coxeter plane | D4 | D3 |
| Graph |  |
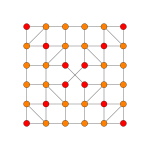 |
| Dihedral symmetry | [6] | [4] |
| Coxeter plane | A5 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
Steriruncic 6-cube
| Steriruncic 6-cube | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t0,2,3{3,33,1} h3,4{4,34} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 7680 |
| Vertices | 1920 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
Alternate names
- Runcicantellated demihexeract/6-demicube
- Prismatorhombated hemihexeract (Acronym prohax) (Jonathan Bowers)[3]
Cartesian coordinates
The Cartesian coordinates for the 1920 vertices of a steriruncic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B6 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12/2] | |
| Coxeter plane | D6 | D5 |
| Graph |  |
 |
| Dihedral symmetry | [10] | [8] |
| Coxeter plane | D4 | D3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
| Coxeter plane | A5 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
Steriruncicantic 6-cube
| Steriruncicantic 6-cube | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t0,1,2,3{3,32,1} h2,3,4{4,34} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 17280 |
| Vertices | 5760 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
Alternate names
- Runcicantitruncated demihexeract/6-demicube
- Great prismated hemihexeract (Acronym gophax) (Jonathan Bowers)[4]
Cartesian coordinates
The Cartesian coordinates for the 5760 vertices of a steriruncicantic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±5,±7)
with an odd number of plus signs.
Images
| Coxeter plane | B6 | |
|---|---|---|
| Graph |  | |
| Dihedral symmetry | [12/2] | |
| Coxeter plane | D6 | D5 |
| Graph |  |
 |
| Dihedral symmetry | [10] | [8] |
| Coxeter plane | D4 | D3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
| Coxeter plane | A5 | A3 |
| Graph |  |
 |
| Dihedral symmetry | [6] | [4] |
Related polytopes
There are 47 uniform polytopes with D6 symmetry, 31 are shared by the B6 symmetry, and 16 are unique:
| D6 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 h{4,34} |
 h2{4,34} |
 h3{4,34} |
 h4{4,34} |
 h5{4,34} |
 h2,3{4,34} |
 h2,4{4,34} |
 h2,5{4,34} | ||||
 h3,4{4,34} |
 h3,5{4,34} |
 h4,5{4,34} |
 h2,3,4{4,34} |
 h2,3,5{4,34} |
 h2,4,5{4,34} |
 h3,4,5{4,34} |
 h2,3,4,5{4,34} | ||||
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "6D uniform polytopes (polypeta)". x3o3o *b3o3x3o - sophax, x3x3o *b3o3x3o - pithax, x3o3o *b3x3x3o - prohax, x3x3o *b3x3x3o - gophax
External links
- Olshevsky, George. "Measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||