Steffen's polyhedron

Steffen's polyhedron
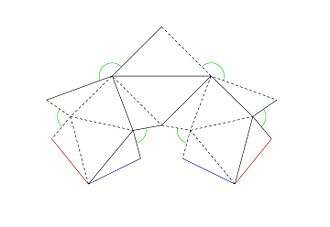
A net for Steffen's polyhedron. The solid and dashed lines represent mountain folds and valley folds, respectively.

In geometry, Steffen's polyhedron is a flexible polyhedron discovered by and named after Klaus Steffen. It is based on the Bricard octahedron, but unlike the Bricard octahedron its surface does not cross itself.[1] With nine vertices, 21 edges, and 14 triangular faces, it is the simplest possible non-crossing flexible polyhedron.[2] Its faces can be decomposed into three subsets: two six-triangle-patches from a Bricard octahedron, and two more triangles (the central two triangles of the net shown in the illustration) that link these patches together.[3] It obeys the strong bellows conjecture, meaning that (like the Bricard octahedron on which it is based) its Dehn invariant stays constant as it flexes.[4]

References

  1. ↑ Connelly, Robert (1981), "Flexing surfaces", in Klarner, David A., The Mathematical Gardner, Springer, pp. 79–89, ISBN 978-1-4684-6688-1, doi:10.1007/978-1-4684-6686-7_10.
  2. ↑ Demaine, Erik D.; O'Rourke, Joseph (2007), "23.2 Flexible polyhedra", Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge, pp. 345–348, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172.
  3. ↑ Fuchs, Dmitry; Tabachnikov, Serge (2007), Mathematical Omnibus: Thirty lectures on classic mathematics, Providence, RI: American Mathematical Society, p. 354, ISBN 978-0-8218-4316-1, MR 2350979, doi:10.1090/mbk/046.
  4. ↑ Alexandrov, Victor (2010), "The Dehn invariants of the Bricard octahedra", Journal of Geometry, 99 (1-2): 1–13, MR 2823098, arXiv:0901.2989 Freely accessible, doi:10.1007/s00022-011-0061-7.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.