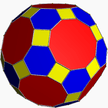
Snub dodecahedron
| Snub dodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 92, E = 150, V = 60 (χ = 2) |
| Faces by sides | (20+60){3}+12{5} |
| Conway notation | sD |
| Schläfli symbols | sr{5,3} or |
| ht0,1,2{5,3} | |
| Wythoff symbol | | 2 3 5 |
| Coxeter diagram | |
| Symmetry group | I, 1/2H3, [5,3]+, (532), order 60 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dihedral angle | 3-3: 164°10′31″ (164.18°) 3-5: 152°55′53″ (152.93°) |
| References | U29, C32, W18 |
| Properties | Semiregular convex chiral |
 Colored faces |
 3.3.3.3.5 (Vertex figure) |
 Pentagonal hexecontahedron (dual polyhedron) |
 Net |
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.
The snub dodecahedron has 92 faces (the most of the 13 Archimedean solids): 12 are pentagons and the other 80 are equilateral triangles. It also has 150 edges, and 60 vertices.
It has two distinct forms, which are mirror images (or "enantiomorphs") of each other. The union of both forms is a compound of two snub dodecahedra, and the convex hull of both forms is a truncated icosidodecahedron.
Kepler first named it in Latin as dodecahedron simum in 1619 in his Harmonices Mundi. H. S. M. Coxeter, noting it could be derived equally from either the dodecahedron or the icosahedron, called it snub icosidodecahedron, with a vertical extended Schläfli symbol and flat Schläfli symbol sr{5,3}.
Cartesian coordinates
Cartesian coordinates for the vertices of a snub dodecahedron are all the even permutations of
- (±2α, ±2, ±2β),
- (±(α + β/φ + φ), ±(−αφ + β + 1/φ), ±(α/φ + βφ − 1)),
- (±(α + β/φ − φ), ±(αφ − β + 1/φ), ±(α/φ + βφ + 1)),
- (±(−α/φ + βφ + 1), ±(−α + β/φ − φ), ±(αφ + β − 1/φ)) and
- (±(−α/φ + βφ − 1), ±(α − β/φ − φ), ±(αφ + β + 1/φ)),
with an even number of plus signs, where
- α = ξ − 1/ξ
and
- β = ξφ + φ2 + φ/ξ,
where φ = 1 + √5/2 is the golden ratio and ξ is the real solution to ξ3 − 2ξ = φ, which is the number:
This snub dodecahedron has an edge length of 4√1+α2 approximately 6.0437380841.
Taking the odd permutations of the above coordinates with an even number of plus signs gives another form, the enantiomorph of the other one. Though it may not be immediately obvious, the figure obtained by taking the even permutations with an even number of plus signs is the same as that obtained by taking the odd permutations with an odd number of plus signs. Similarly, the mirror image has either an odd permutation with an even number of plus signs or an even permutation with an odd number of plus signs.
Surface area and volume

For a snub dodecahedron whose edge length is 1, the surface area is
and the volume is
where φ is the golden ratio.
The snub dodecahedron has the highest sphericity (about 0.982) of all Archimedean solids.
Orthogonal projections


The snub dodecahedron has two special orthogonal projections, centered on two types of faces: triangles and pentagons, corresponding to the A2 and H2 Coxeter planes.
| Centered by | Face Triangle |
Face Pentagon |
Edge |
|---|---|---|---|
| Image |  |
 |
 |
| Projective symmetry |
[3] | [5]+ | [2] |
| Dual image |
 |
 |
 |
Geometric relations
The snub dodecahedron can be generated by taking the twelve pentagonal faces of the dodecahedron and pulling them outward so they no longer touch. At a proper distance this can create the rhombicosidodecahedron by filling in square faces between the divided edges and triangle faces between the divided vertices. But for the snub form, only add the triangle faces and leave the square gaps empty. Then apply an equal rotation to the centers of the pentagons and triangles, continuing the rotation until the gaps can be filled by two equilateral triangles.
 Dodecahedron |
 Rhombicosidodecahedron (Expanded dodecahedron) |
 Snub dodecahedron |
The snub dodecahedron can also be derived from the truncated icosidodecahedron by the process of alternation. Sixty of the vertices of the truncated icosidodecahedron form a polyhedron topologically equivalent to one snub dodecahedron; the remaining sixty form its mirror-image. The resulting polyhedron is vertex-transitive but not uniform, because its edges are of unequal lengths; some deformation is required to transform it into a uniform polyhedron.
Related polyhedra and tilings
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
 |
 |
 |
 |
 |
 |
 | |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
This semiregular polyhedron is a member of a sequence of snubbed polyhedra and tilings with vertex figure (3.3.3.3.n) and Coxeter–Dynkin diagram ![]()
![]()
![]()
![]()
![]() . These figures and their duals have (n32) rotational symmetry, being in the Euclidean plane for n = 6, and hyperbolic plane for any higher n. The series can be considered to begin with n = 2, with one set of faces degenerated into digons.
. These figures and their duals have (n32) rotational symmetry, being in the Euclidean plane for n = 6, and hyperbolic plane for any higher n. The series can be considered to begin with n = 2, with one set of faces degenerated into digons.
| n32 symmetry mutations of snub tilings: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry n32 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Snub figures |
 |
 |
 |
 |
 |
 |
 |
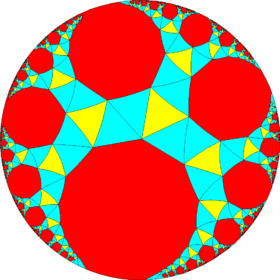 |
| Config. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Gryro figures |
 |
 |
 |
 |
 |
 |
 | |
| Config. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Snub dodecahedral graph
| Snub dodecahedral graph | |
|---|---|
|
5-fold symmetry Schlegel diagram | |
| Vertices | 60 |
| Edges | 150 |
| Automorphisms | 60 |
| Properties | Hamiltonian, regular |
In the mathematical field of graph theory, a snub dodecahedral graph is the graph of vertices and edges of the snub dodecahedron, one of the Archimedean solids. It has 60 vertices and 150 edges, and is an Archimedean graph.[1]
 |
 |
 |
See also
- Planar polygon to polyhedron transformation animation
- ccw and cw spinning snub dodecahedron
References
- ↑ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. 89 (514): 76–81.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
External links
- Eric Wolfgang Weisstein, Snub dodecahedron (Archimedean solid) at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra s3s5s - snid".
- Editable printable net of a Snub Dodecahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- The Snub Dodecahedron made with LEGO by Antonio Nicassio (ITALY)