Semiconductor laser theory

Semiconductor lasers (520nm, 445nm, 635nm)

Semiconductor lasers (660nm, 532nm, 405nm)

Semiconductor lasers or laser diodes play an important part in our everyday lives by providing cheap and compact-size lasers. They consist of complex multi-layer structures requiring nanometer scale accuracy and an elaborate design. Their theoretical description is important not only from a fundamental point of view, but also in order to generate new and improved designs. It is common to all systems that the laser is an inverted carrier density system. The carrier inversion results in an electromagnetic polarization which drives an electric field . In most cases, the electric field is confined in a resonator, the properties of which are also important factors for laser performance.

Gain medium

Comparison of gain and absorption calculated in Hartree–Fock approximation (dotted line) and fully taking into account collision terms (solid line). The sample is a Ga(AsSb) quantum well surrounded by GaAs spacers. For the top figure, a density of 1.3 x 10¹² cm⁻² was used which is well above lasing threshold. For the bottom figure, the carrier density is negligible. The differences in lineshape are obvious especially for the lasing structure. The Hartree–Fock approximation leads to absorption below the bandgap (below about 0.94 eV), which is a natural consequence of the relaxation time approximation, but is completely unphysical. For the low density case, the T₂-time approximation also leads to extended tails.

In semiconductor laser theory, the optical gain is produced in a semiconductor material. The choice of material depends on the desired wavelength and properties such as modulation speed. It may be a bulk semiconductor, but more often a quantum heterostructure. Pumping may be electrically or optically (disk laser). All these structures can be described in a common framework and in differing levels of complexity and accuracy.^[1]

Light is generated in a semiconductor laser by radiative recombination of electrons and holes. In order to generate more light by stimulated emission than is lost by absorption, the system has to be inverted, see the article on lasers. A laser is, thus, always a high carrier density system that entails many-body interactions. These cannot be taken into account exactly because of the high number of particles involved. Various approximations can be made:

• Free carrier model: In simple models, many-particle interactions are often neglected. The carrier plasma is then simply seen as a reservoir which relaxes the carrier distributions. However, the many body interaction is necessary to produce the correct linewidth. Therefore, at the free carrier level a scattering time has to be introduced phenomenologically, usually extracted from experiment, but will change with carrier density and temperature. Simple models for the gain coefficient are often used to obtain a system of laser diode rate equations, enabling one to dynamically calculate the time-dependent laser response. An expression for the free-carrier gain is given in the article on semiconductor optical gain.
• Hartree Fock approximation: To describe an interacting carrier system at any density, the semiconductor Bloch equations^[2][3] (SBEs) may be employed. These may be solved in the Hartree–Fock approximation.^[4] In this case, carrier–carrier interaction leads to renormalisation terms for band structure and electric field. The collision terms, i.e., the terms describing carrier–carrier scattering, still do not occur and have to be introduced phenomenologically using a relaxation time or T₂-time for the polarization.
• Correlation effects: Taking the collision terms into account explicitly requires a large numerical effort, but can be done with state-of-the-art computers.^[5] Technically speaking, the collision terms in the semiconductor Bloch equations are included in second-Born approximation.^[3] This microscopic model has the advantage of having predictive character, i.e., it yields the correct linewidth for any temperature or excitation density. In the other models, the relaxation time has to be extracted from experiment, but depends on the actual parameters meaning the experiment has to be redone for any temperature and excitation intensity.

The above-mentioned models yield the polarization of the gain medium. From this, the absorption or gain may be calculated via

Optical absorption

where denotes the photon energy, is the background refractive index, is the vacuum speed of light, and are the vacuum permittivity and background dielectric constant, respectively, and is the electric field present in the gain medium. "" denotes the imaginary part of the quantity in brackets. The above formula can be derived from Maxwell's equations.^[3]

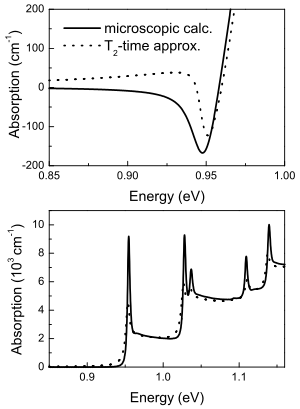
The figure shows a comparison of the calculated absorption spectra for high density where absorption becomes negative (gain) and low density absorption for the two latter theoretical approaches discussed. The differences in lineshape for the two theoretical approaches are obvious especially for the high carrier density case which applies to a laser system. The Hartree–Fock approximation leads to absorption below the bandgap (below about 0.94 eV), which is a natural consequence of the relaxation time approximation, but is completely unphysical. For the low density case, the T₂-time approximation also overestimates the strength of the tails.

Laser resonator

A resonator is usually part of a semiconductor laser. Its effects have to be taken into account in the calculation. Therefore, the eigenmode expansion of the electric field is done not in plane waves but in the eigenmodes of the resonator which may be calculated, e.g., via the transfer-matrix method in planar geometries; more complicated geometries often require the use of full Maxwell-equations solvers (finite-difference time-domain method). In the laser diode rate equations, the photon life time enters instead of the resonator eigenmodes. In this approximative approach, may be calculated from the resonance mode^[6] and is roughly proportional to the strength of the mode within the cavity. Fully microscopic modeling of laser emission can be performed with the semiconductor luminescence equations^[7] where the light modes enter as an input. This approach includes many-body interactions and correlation effects systematically, including correlations between quantized light and the excitations of the semiconductor. Such investigations can be extended to studying new intriguing effects emerging in semiconductor quantum optics.

See also

• Semiconductor Bloch equations
• Semiconductor luminescence equations
• Semiconductor optical gain
• Coherent effects in semiconductor optics
• Quantum-optical spectroscopy
• Lasers
• Laser spectroscopy
• Nonlinear theory of semiconductor lasers

References

Further reading

• Chow, W. W.; Koch, S. W. (2011). Semiconductor-Laser fundamentals. Springer. ISBN 978-3540641667. 
• Haug, H.; Koch, S. W. (2009). Quantum Theory of the Optical and Electronic Properties of Semiconductors (5th ed.). World Scientific. p. 216. ISBN 9812838848. 
• Siegman, A. E. (1986). Lasers. Univ. Science Books. ISBN 978-0935702118. 
• Demtröder, W. (2008). Laser Spectroscopy: Vol. 1: Basic Principles. Springer. ISBN 978-3540734154. 
• Demtröder, W. (2008). Laser Spectroscopy: Vol. 2: Experimental Techniques. Springer. ISBN 978-3540749523.