Self-ionization of water

| Acids and bases |
|---|
| Acid types |
| Base types |
The self-ionization of water (also autoionization of water, and autodissociation of water) is an ionization reaction in pure water or in an aqueous solution, in which a water molecule, H2O, deprotonates (loses the nucleus of one of its hydrogen atoms) to become a hydroxide ion, OH−. The hydrogen nucleus, H+, immediately protonates another water molecule to form hydronium, H3O+. It is an example of autoprotolysis, and exemplifies the amphoteric nature of water.
Equilibrium constant
Chemically pure water has an electrical conductivity of 0.055 µS/cm. According to the theories of Svante Arrhenius, this must be due to the presence of ions. The ions are produced by the self-ionization reaction
- H2O + H2O ⇌ H3O+ + OH−
This equilibrium applies to pure water and any aqueous solution.
Expressed with chemical activities a, instead of concentrations, the thermodynamic equilibrium constant for the water ionization reaction is:
which is numerically equal to the more traditional thermodynamic equilibrium constant written as:
under the assumption that the sum of the chemical potentials of H+ and H3O+ is formally equal to twice the chemical potential of H2O at the same temperature and pressure.[1]
Because most acid–base solutions are typically very dilute, the activity of water is generally approximated as being equal to unity, which allows the ionic product of water to be expressed as:[2]
In dilute aqueous solutions, the activities of the solute particles are approximately equal to their concentrations. Thus, the ionization constant, dissociation constant, self-ionization constant, or ionic product of water, symbolized by Kw, may be given by:
where [H3O+] is the molality (≈molar concentration)[3] of hydrogen or hydronium ion, and [OH−] is the concentration of hydroxide ion. When the equilibrium constant is written as a product of concentrations (as opposed to activities) it is necessary to make corrections to the value of depending on ionic strength and other factors (see below).[4]
At 25 °C and zero ionic strength, Kw is equal to 1.0×10−14. Note that as with all equilibrium constants, the result is dimensionless because the concentration is in fact a concentration relative to the standard state, which for H+ and OH− are both defined to be 1 molal (or molar). For most practical purposes, the molal and molar concentrations are equal near the ambient temperature and pressure. The molal concentration scale results in concentration values which account for density changes with temperature or pressure changes; therefore, it is the scale used in precise or nonambient applications, e.g., for seawater,[3] or at elevated temperatures, like those in thermal power plants.
We can also define pKw = −log10 Kw = 14 at 25 °C. This is analogous to the notations pH and pKa for an acid dissociation constant, where the symbol p denotes a cologarithm. The logarithmic form of the equilibrium constant equation is pKw = pH + pOH.
Dependence on temperature, pressure and ionic strength
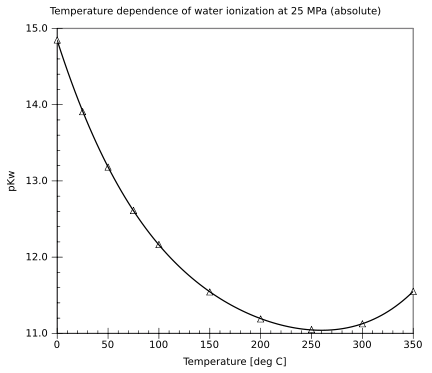 Temperature dependence of the water ionization constant at 25 MPa |
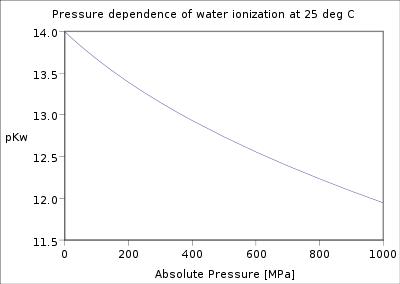 Pressure dependence of the water ionization constant at 25 °C |
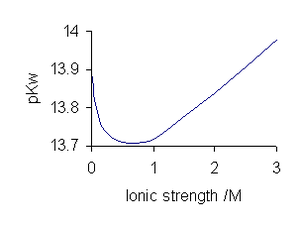 Variation of pKw with ionic strength of NaCl solutions at 25 °C |
The dependence of the water ionization on temperature and pressure has been investigated thoroughly.[5] The value of pKw decreases as temperature increases from the melting point of ice to a minimum at c. 250 °C, after which it increases up to the critical point of water c. 374 °C. It decreases with increasing pressure.
| Temperature | Pressure[7] | pKw |
|---|---|---|
| 0 °C | 0.10 MPa | 14.95 |
| 25 °C | 0.10 MPa | 13.99 |
| 50 °C | 0.10 MPa | 13.26 |
| 75 °C | 0.10 MPa | 12.70 |
| 100 °C | 0.10 MPa | 12.25 |
| 150 °C | 0.47 MPa | 11.64 |
| 200 °C | 1.5 MPa | 11.31 |
| 250 °C | 4.0 MPa | 11.20 |
| 300 °C | 8.7 MPa | 11.34 |
| 350 °C | 17 MPa | 11.92 |
With electrolyte solutions, the value of pKw is dependent on ionic strength of the electrolyte. Values for sodium chloride are typical for a 1:1 electrolyte. With 1:2 electrolytes, MX2, pKw decreases with increasing ionic strength.[8]
The value of Kw is usually of interest in the liquid phase. Example values for superheated steam (gas) and supercritical water fluid are given in the table.
Comparison of pKw values for liquid water, superheated steam, and supercritical water.[1] Temp.Pressure350 °C 400 °C 450 °C 500 °C 600 °C 800 °C 0.1 MPa 47.961b 47.873b 47.638b 46.384b 40.785b 17 MPa 11.920 (liquid)a 25 MPa 11.551 (liquid)c 16.566 18.135 18.758 19.425 20.113 100 MPa 10.600 (liquid)c 10.744 11.005 11.381 12.296 13.544 1000 MPa 8.311 (liquid)c 8.178 8.084 8.019 7.952 7.957 - Notes to the table. The values are for supercritical fluid except those marked: a at saturation pressure corresponding to 350 °C. b superheated steam. c compressed or subcooled liquid.
Isotope effects
Heavy water, D2O, self-ionizes less than normal water, H2O;
- D2O + D2O ⇌ D3O+ + OD−
This is attributed to oxygen forming a slightly stronger bond to deuterium because the larger mass of deuterium results in a lower zero-point energy, a quantum mechanical effect analogous to the kinetic isotope effect.
Expressed with activities a, instead of concentrations, the thermodynamic equilibrium constant for the heavy water ionization reaction is:
Assuming the activity of the D2O to be 1, and assuming that the activities of the D3O+ and OD− are closely approximated by their concentrations
The following table compares the values of pKw for H2O and D2O.[9]
pKw values for pure water T/°C 10 20 25 30 40 50 H2O 14.535 14.167 13.997 13.830 13.535 13.262 D2O 15.439 15.049 14.869 14.699 14.385 14.103
Ionization equilibria in water–heavy water mixtures
In water–heavy water mixtures equilibria several species are involved: H2O, HDO, D2O, H3O+, D3O+, H2DO+, HD2O+, HO−, DO−.
Mechanism
The rate of reaction for the ionization reaction
- 2 H2O → H3O+ + OH−
depends on the activation energy, ΔE‡. According to the Boltzmann distribution the proportion of water molecules that have sufficient energy, due to thermal population, is given by
where k is the Boltzmann constant. Thus some dissociation can occur because sufficient thermal energy is available. The following sequence of events has been proposed on the basis of electric field fluctuations in liquid water.[10] Random fluctuations in molecular motions occasionally (about once every 10 hours per water molecule[11]) produce an electric field strong enough to break an oxygen–hydrogen bond, resulting in a hydroxide (OH−) and hydronium ion (H3O+); the hydrogen nucleus of the hydronium ion travels along water molecules by the Grotthuss mechanism and a change in the hydrogen bond network in the solvent isolates the two ions, which are stabilized by solvation. Within 1 picosecond, however, a second reorganization of the hydrogen bond network allows rapid proton transfer down the electric potential difference and subsequent recombination of the ions. This timescale is consistent with the time it takes for hydrogen bonds to reorientate themselves in water.[12][13][14]
The inverse recombination reaction
- H3O+ + OH− → 2 H2O
is among the fastest chemical reactions known, with a reaction rate constant of 1.3×1011 M−1 s−1 at room temperature. Such a rapid rate is characteristic of a diffusion-controlled reaction, in which the rate is limited by the speed of molecular diffusion.[15]
Relationship with the neutral point of water
Water molecules dissociate into equal amounts of H3O+ and OH−, so their concentrations are equal to 1.00×10−7 mol dm−3 at 25 °C. A solution in which the H3O+ and OH− concentrations equal each other is considered a neutral solution. In general, the pH of the neutral point is numerically equal to 1/2pKw.
Pure water is neutral, but most water samples contain impurities. If an impurity is an acid or base, this will affect the concentrations of hydronium ion and hydroxide ion. Water samples that are exposed to air will absorb some acidic carbon dioxide to form carbonic acid (H2CO3) and the concentration of H3O+ will increase due to the reaction H2CO3 + H2O = HCO3− + H3O+. The concentration of OH− will decrease in such a way that the product [H3O+][OH−] remains constant for fixed temperature and pressure. Thus these water samples will be slightly acidic. If a pH of exactly 7.0 is required, it must be maintained with an appropriate buffer solution.
See also
References
- 1 2 "Release on the Ionization Constant of H2O" (PDF). Lucerne: The International Association for the Properties of Water and Steam. August 2007.
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "autoprotolysis constant".
- 1 2 Stumm, Werner; Morgan, James (1996). Aquatic Chemistry. Chemical Equilibria and Rates in Natural Waters (3rd ed.). John Wiley & Sons, Inc. ISBN 9780471511847.
- ↑ Harned, H. S.; Owen,, B. B. (1958). The Physical Chemistry of Electrolytic Solutions (3rd ed.). New York: Reinhold. p. 635.
- ↑ International Association for the Properties of Water and Steam (IAPWS)
- ↑ Bandura, Andrei V.; Lvov, Serguei N. (2006). "The Ionization Constant of Water over Wide Ranges of Temperature and Density" (PDF). Journal of Physical and Chemical Reference Data. 35 (1): 15–30. doi:10.1063/1.1928231.
- ↑ 0.1 MPa for T < 100 °C. Saturation pressure for T > 100 °C.
- ↑ Harned, H. S.; Owen,, B. B. (1958). The Physical Chemistry of Electrolytic Solutions (3rd ed.). New York: Reinhold. pp. 634–649, 752–754.
- ↑ Lide, D. R., ed. (1990). CRC Handbook of Chemistry and Physics (70th ed.). Boca Raton (FL):CRC Press.
- ↑ Geissler, P. L.; Dellago, C.; Chandler, D.; Hutter, J.; Parrinello, M. (2001). "Autoionization in liquid water". Science. 291 (5511): 2121–2124. Bibcode:2001Sci...291.2121G. PMID 11251111. doi:10.1126/science.1056991.
- ↑ Eigen, M.; De Maeyer, L. (1955). "Untersuchungen über die Kinetik der Neutralisation I" [Investigations on the kinetics of neutralization I]. Z. Elektrochem. 59: 986.
- ↑ Stillinger, F. H. (1975). "Theory and Molecular Models for Water". Adv. Chem. Phys. 31: 1. doi:10.1002/9780470143834.ch1.
- ↑ Rapaport, D. C. (1983). "Hydrogen bonds in water". Mol. Phys. 50 (5): 1151. Bibcode:1983MolPh..50.1151R. doi:10.1080/00268978300102931.
- ↑ Chen, S.-H.; Teixeira, J. (1986). "Structure and Dynamics of Low-Temperature Water as Studied by Scattering Techniques". Adv. Chem. Phys. 64: 1. doi:10.1002/9780470142882.ch1.
- ↑ Tinoco, I.; Sauer, K.; Wang, J. C. (1995). Physical Chemistry: Principles and Applications in Biological Sciences (3rd ed.). Prentice-Hall. p. 386.
External links
- General Chemistry – Autoionization of Water