Ruppert's algorithm
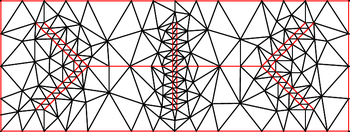
In mesh generation, Ruppert's algorithm, also known as Delaunay refinement, is an algorithm for creating quality Delaunay triangulations. The algorithm takes a planar straight-line graph (or in dimension higher than two a piecewise linear system) and returns a conforming Delaunay triangulation of only quality triangles. A triangle is considered poor-quality if it has a circumradius to shortest edge ratio larger than some prescribed threshold. Discovered by Jim Ruppert in the early 1990s,[1] "Ruppert's algorithm for two-dimensional quality mesh generation is perhaps the first theoretically guaranteed meshing algorithm to be truly satisfactory in practice."[2]
Motivation
When doing computer simulations such as computational fluid dynamics, one starts with a model such as a 2D outline of a wing section. The input to a 2D finite element method needs to be in the form of triangles that fill all space, and each triangle to be filled with one kind of material – in this example, either "air" or "wing". Long, skinny triangles cannot be simulated accurately. The simulation time is generally proportional to the number of triangles, and so one wants to minimize the number of triangles, while still using enough triangles to give reasonably accurate results – typically by using an unstructured grid. The computer uses Ruppert's algorithm (or some similar meshing algorithm) to convert the polygonal model into triangles suitable for the finite element method.
Algorithm description
The algorithm begins with a Delaunay triangulation of the input vertices and then consists of two main operations.
- The midpoint of a segment with non-empty diametral circles is inserted into the triangulation.
- The circumcenter of a poor-quality triangle is inserted into the triangulation, unless this circumcenter lies in the diametral circle of some segment. In this case, the encroached segment is split instead.
These operations are repeated until no poor-quality triangles exist and all segments are not encroached.
Pseudocode
1 function Ruppert(points,segments,threshold): 2 T := DelaunayTriangulation(points); 3 Q := the set of encroached segments and poor quality triangles; 4 while Q is not empty: // The main loop 5 if Q contains a segment s: 6 insert the midpoint of s into T; 7 else Q contains poor quality triangle t: 8 if the circumcenter of t encroaches a segment s: 9 add s to Q; 10 else: 11 insert the circumcenter of t into T; 12 end if; 13 end if; 14 update Q; 15 end while; 16 return T; 17 end Ruppert.
Practical usage
Without modification Ruppert's algorithm is guaranteed to terminate and generate a quality mesh for non-acute input and any poor-quality threshold less than about 20.7 degrees. To relax these restrictions various small improvements have been made. By relaxing the quality requirement near small input angles, the algorithm can be extended to handle any straight-line input.[3] Curved input can also be meshed using similar techniques.[4] Ruppert's algorithm can be naturally extended to three dimensions, however its output guarantees are somewhat weaker due to the sliver type tetrahedron.
An extension of Ruppert's algorithm in two dimensions is implemented in the freely available Triangle package. Two variants of Ruppert's algorithm in this package are guaranteed to terminate for a poor-quality threshold of about 26.5 degrees.[5] In practice these algorithms are successful for poor-quality thresholds over 30 degrees. However, examples are known which cause the algorithm to fail with a threshold greater than 29.06 degrees.[6]
See also
References
- ↑ Ruppert, Jim (1995). "A Delaunay refinement algorithm for quality 2-dimensional mesh generation". Journal of Algorithms. 18 (3): 548–585. doi:10.1006/jagm.1995.1021.
- ↑ Shewchuk, Jonathan. "Ruppert's Delaunay Refinement Algorithm". Retrieved April 2010. Check date values in:
|access-date=(help) - ↑ Miller, Gary; Pav, Steven; Walkington, Noel (2005). "When and why Delaunay refinement algorithms work". International Journal of Computational Geometry and Applications. 15 (1): 25–54. doi:10.1142/S0218195905001592.
- ↑ Pav, Steven; Walkington, Noel (2005). Delaunay refinement by corner lopping. Proceedings of the 14th International Meshing Roundtable. pp. 165–181.
- ↑ Shewchuk, Jonathan (2002). "Delaunay refinement algorithms for triangular mesh generation". Computational Geometry: Theory and Applications. 22 (1–3): 21–74. doi:10.1016/s0925-7721(01)00047-5.
- ↑ Rand, Alexander (2011). "Improved Examples of Non-Termination for Ruppert's Algorithm". arXiv:1103.3903
 [cs.CG]..
[cs.CG]..
External links
- Rineau, Laurent. "2D Conforming Triangulations and Meshes". Retrieved April 2010. Check date values in:
|access-date=(help)
- Shewchuk, Jonathan. "Triangle: A Two-Dimensional Quality Mesh Generator and Delaunay Triangulator.". Retrieved April 2010. Check date values in:
|access-date=(help)
- Si, Hang. "TetGen: A Quality Tetrahedral Mesh Generator and a 3D Delaunay Triangulator". Retrieved September 2014. Check date values in:
|access-date=(help)