Ruling gradient

The term ruling grade is usually used as a synonym for "steepest climb" between two points on a railroad. More simply, the steepest grade to be climbed dictates how powerful the locomotive must be (or how light the train) in order to complete the run without assistance. Even if 99% of the line could be run with a light (and cheap) locomotive, if at some point on the line there is a steeper gradient that a light engine would be unable to climb, this gradient "rules" that a more powerful (and expensive) locomotive must be used, in spite of it being far too powerful for the rest of the line. This is why special "helper engines" (also dubbed "Bankers") are often stationed near steep grades on otherwise mild tracks, because it is cheaper than running a too-powerful locomotive over the entire track mileage just in order to make the grade, especially when multiple trains run over the line each day.

In the 1953 edition of Railway Engineering William H. Hay says "The ruling grade may be defined as the maximum gradient over which a tonnage train can be hauled with one locomotive....The ruling grade does not necessarily have the maximum gradient on the division. Momentum grades, pusher grades, or those that must regularly be doubled by tonnage trains may be heavier." This means the "ruling grade" may change if the management chooses to operate the railroad differently.

In steam days Southern Pacific trains eastward across Nevada and Utah faced nothing steeper than 0.43% in the 531 miles from Sparks to Ogden—except for a few miles of 1.4% east of Wells. Trains would leave Sparks with enough engine to manage the 0.43% grade (e.g. a 2-10-2 with 5500 tons) and would get helper engines at Wells; the "ruling grade" from Sparks to Ogden could be considered 0.43%. But nowadays the railroad doesn't base helper engines and crews at Wells so trains must leave Sparks with enough power to climb the 1.4%, making that the division's ruling grade.

So the term is always ambiguous, and is more ambiguous still if the ruling grade is a momentum grade. Overland Route trains from Sacramento, California to Oakland face nothing steeper than 0.5% on Track 1, the traditional westward track, but nowadays they might need to climb to the Benicia bridge on Track 2 which includes 0.7 mile at about 1.9%, preceded and followed by near-level track. How to define "ruling grade" there? Should we assume a running start? How much of one? If we don't assume a running start, what train length should we assume, many freight trains being longer than the hill?

(And if we do assume a running start at some arbitrary speed, the calculated "ruling grade" will be different for locomotives having different power-vs-speed characteristics.)

In North America, Congress set the Standard Grade for railroads eligible for subsidies and grants in the 1850s. They took as that standard the one adopted by the Cumberland - Wheeling Railway, that grade being 116 feet per mile. Later when charters were drawn up for the Union Pacific Railroad and the Canadian Pacific Railway in Canada, the national governments imposed the Standard Ruling Grade on the two lines because both received federal assistance and regulation. (Vance, JE Jr.,1995)

Compensation for curvature

Other things being equal, a train is harder to pull around a curve than it is on straight track because the wagons - especially bogie (2 axle) wagons - try to follow the chord of the curve and not the arc. To compensate for this, the gradient should be a little less steep the sharper the curve is; the necessary grade reduction is assumed to be given by a simple formula such as 0.04 per cent per "degree of curve", the latter being a measure of curve sharpness used in the United States. On a 10-degree curve (radius 573.7 feet) the grade would thus need to be 0.4% less than the grade on straight track.

Compensation for gradients in tunnels

Tunnels on steep gradients can present problems for air-breathing locomotives, such as steam locomotives and diesel locomotives. Poor ventilation in long or narrow tunnels can starve the locomotive of power. The solution is analogous to compensation for curvature and requires the gradient in the tunnel and for some distance on either side to be greatly reduced compared to the ruling grade. Unfortunately, the necessary compensation for gradient is not a simple equation, but is rather a trial and error process. Since one cannot build several tunnels to find out which one is best, it is useful to study existing tunnels with steep gradients.

Moisture from exhausts and springs can also make the rails slippery, and allowance may need to be taken for that as well.

Case Study - Cascade Tunnel, Washington, US

As happened on the first Cascade Tunnel, too little compensation for tunnel gradient was made. It is worthwhile even in hindsight to consider how else the problem might have been addressed.

Tunnel 1 as built

The lines approaching the first cascade tunnel had a ruling gradient of 2.2% (1 in 45.5), while the tunnel itself had a gradient of 1.7% (1 in 58.8) facing eastbound trains. This gradient appears to be chosen by the expedient of building the shortest possible tunnel that connected with the original switchback route connecting Tye (Wellington) (West) at 955 m and Cascade Tunnel Station (East) at 1031 m. The higher portal of the 13,873 feet (4,228 m) long tunnel was 305 feet (93 m) higher than the lower portal. Even though the ruling gradient in the tunnel was (slightly) less than that on the tracks on either side, the first Cascade tunnel soon proved to have problems with fumes, which were later resolved by electrification.

Tunnel 1 as might have been

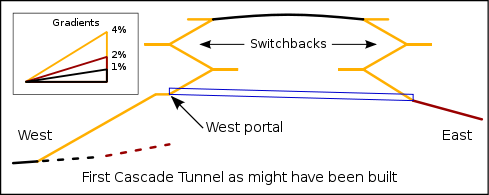
The gradient problem in the first tunnel is the result of the western portal being 100 metres lower than the eastern end, assuming that the tunnel joins the switchback route at the first available opportunity. If the 4% gradients at the western end had started several kilometres earlier, then the western portal could have been 100 m higher, making the first tunnel practically level and free of smoke problems. Strictly speaking, the level gradient should continue for a suitable distance beyond the portal, so that eastbound trains crawling up the hill can accelerate to line speed by the time that they enter the tunnel, so that the passage through whole of the tunnel uses the minimum throttle and generates minimum smoke.

The tunnel should have a slight gradient to facilitate drainage of water.

Open air grade

Since in the open air, as many engines as needed can be added to a train to overcome a steep gradient, a better solution would have been to have a level tunnel from "New Tye" (West) to Cascade Tunnel Station (West), with a 2.6 mile stretch of say 4% gradient ( 1 in 25 ) on the western approaches from say Windy Point Tunnel. The New Tye would have been about 250 feet higher in elevation. Levelling the main tunnel at the Cascade Tunnel Station is likely to require extra tunnel because the elevation of the valleys are higher.

Should the new steep approaches ever become operationally inconvenient, then it might be replaced by say, a spiral tunnel. Unlike the main 2.6 mile tunnel, which can only be replaced on an all or nothing basis, an inadequate approach can be replaced in dribs and drabs.

A level main tunnel would have avoided the need for electrification of the main tunnel to eliminate the smoke problem, and perhaps even eliminated the need for a second longer tunnel later on.

Lapstone Zig Zag deviation tunnel (1892), NSW, Australia

The original zig zag at Lapstone, near Sydney, was constructed in 1869, to avoid having to build a long tunnel.

The Lapstone Zig Zag became a bottleneck because, among other reasons, the length of the top and bottom roads restricted train lengths. A single-track tunnel was built in 1892 to replace the zig zag. However, this tunnel was on a steep gradient, with a ruling grade of 1 in 33, which caused problems with the smoke from hard-working locomotives. These problems pre-dated the fume problems with the first Cascade Tunnel on the opposite side of the world.

By 1908, the situation had become unbearable, and with the need to duplicate the line, the old single-track tunnel was replaced by an almost tunnel-free alignment, with a reduced ruling grade of 1 in 60.

Lithgow Zig Zag deviation tunnels (1910), NSW, Australia

The original Lithgow Zig Zag was built in 1869, when the colony of New South Wales had limited tunnel building resources, and the Zig Zag became something of a wonder of the world.

By the 1900s, the single track Zig Zag had become a bottleneck, and duplication of the line became essential. By careful alignment of the new line to exploit a large number of clefts in the terrain, a double track deviation with 10 short tunnels was possible rather than one long one. These tunnels have a relatively gentle gradient of 1 in 90 (1.11%). However, the frequent gaps between the tunnels provide good natural ventilation. In the latter days of steam, a train with 4 locomotives might haul a train to the entrance of the ten tunnels, with only 2 locomotives having to proceed through the tunnels themselves. Thus the fume problems in these tunnels was moderate.

Woodhead tunnel (1845), England, UK

The Woodhead Tunnel was summit tunnel of 3 miles (4.8 km) length and suffered from poor working conditions as the gradient of 1 in 200 (0.5%) in the tunnel was not sufficiently reduced compared to the 1 in 100 (1%) ruling grade of the approaches as a whole. The tunnel actually consisted of two separate bores, of minimum cross-section.

Woy Woy tunnel (1888), NSW, Australia

The Woy Woy tunnel in New South Wales is approximately 2000 m long. It is straight and level, and double track. The tunnel is near sea-level, which partly explains why it is near level. There are no intermediate ventilation shafts. There are short rising grades of 1 in 40 and 1 in 80 on either side of the tunnel. The ruling grade of the line is 1 in 40, and taking all these factors into account, the tunnel has never suffered heavily from smoke. In all, a reasonably well designed tunnel. The line was electrified in 1961, but since the 1990s freight trains have reverted to diesel haulage.

Ardglen Tunnel, NSW, Australia

Ardglen Tunnel is a 487 m (1,598 ft) long tunnel at the summit located at a low point at top of the Great Dividing Range. It is approached by steep 1 in 40 gradients (2.5%) in both directions. Heavy traffic predominates in the south bound direction. The tunnel is level, though the rear portion of a long trains would still be struggling up the steep grade while the engine is still in the tunnel.[1]

This tunnel is located at the Great Dividing Range. This tunnel was notorious for its lack of air and severe heat. [2][3]

Summits

A ruling grade is often found at a long climb up to a summit. Ideally, the cutting at the summit should be as deep as possible, such as at Shap, as this helps reduce the amount of climb, and the steepness of the gradient. Alternately, a summit tunnel should be provided, such as at Ardglen.

Selective momentum

The faster a train can go, the more momentum it has, and the less of a problem a steep gradient is.

Train speeds may however be restricted by light track. It tends to be the case that the lightness of the track will be uniform throughout an operating district.

If the track is upgraded approaching a steep gradient, train speeds and momentum may be raised just where it is needed most. This needs heavier rails, more sleepers, and more fixtures.

Curve and Gradient Books

Other tunnels

See also

References

  1. ↑ Tunnel on Australian Railways, by William A. Bailey, Austrail Publications, 1974, page 9
  2. ↑ Tunnel on Australian Railways, by William A. Bailey, Austrail Publications, 1974, page 9
  3. ↑ ARTC Curve & Gradient page 11
  4. ↑ Archived December 8, 2008, at the Wayback Machine.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.