Reeve tetrahedron

Reeve tetrahedron

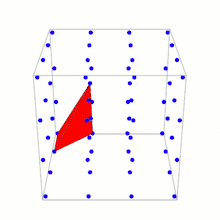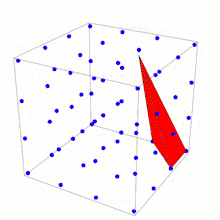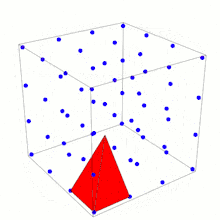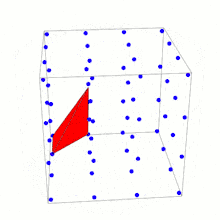
In geometry, the Reeve tetrahedron is a polyhedron, named after John Reeve, in $ℝ 3$ with vertices at $(0, 0, 0)$ , $(1, 0, 0)$ , $(0, 1, 0)$ and $(1, 1, r)$ where $r$ is a positive integer. Each vertex lies on a fundamental lattice point (a point in $ℤ 3$ ). No other fundamental lattice points lie on the surface or in the interior of the tetrahedron. In 1957 Reeve used this tetrahedron as a counterexample to show that there is no simple equivalent of Pick's theorem in $ℝ 3$ or higher-dimensional spaces.^[1] This is seen by noticing that Reeve tetrahedra have the same number of interior and boundary points (0 and 4) for any value of $r$ , but different volumes.

The Ehrhart polynomial of the Reeve tetrahedron $T r$ of height $r$ is

L({\mathcal {T}}_{r},t)={\frac {r}{6}}t^{3}+t^{2}+\left(2-{\frac {r}{6}}\right)t+1.

^[2]

Thus, for $r \geq 13$ , the Ehrhart polynomial of $T r$ has a negative coefficient.

Notes

↑ Reeve, J. E. "On the Volume of Lattice Polyhedra". Proceedings of the London Mathematical Society. s3–7 (1): 378–395.
↑ Beck, Matthias; Robins, Sinai (2007). Computing the Continuous Discretely. New York: Springer. p. 75.

References

Kołodziejczyk, Krzysztof (1996). "An 'Odd' Formula for the Volume of Three-Dimensional Lattice Polyhedra". Geometriae Dedicata. 61: 271–278.
Beck, Matthias; Robins, Sinai (2007). Computing the Continuous Discretely, Integer-point enumeration in polyhedra. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 978-0-387-29139-0. MR 2271992.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.