Range tree

Range tree
Type tree
Invented 1979
Invented by Jon Louis Bentley
Time complexity in big O notation
Algorithm Average Worst Case

In computer science, a range tree is an ordered tree data structure to hold a list of points. It allows all points within a given range to be reported efficiently, and is typically used in two or higher dimensions. Range trees were introduced by Jon Louis Bentley in 1979.[1] Similar data structures were discovered independently by Lueker,[2] Lee and Wong,[3] and Willard.[4] The range tree is an alternative to the k-d tree. Compared to k-d trees, range trees offer faster query times of (in Big O notation) but worse storage of , where n is the number of points stored in the tree, d is the dimension of each point and k is the number of points reported by a given query.

Bernard Chazelle improved this to query time and space complexity .[5][6]

Description

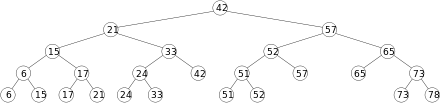
An example of a 1-dimensional range tree.
An example of a 1-dimensional range tree.

A range tree on a set of 1-dimensional points is a balanced binary search tree on those points. The points stored in the tree are stored in the leaves of the tree; each internal node stores the largest value contained in its left subtree. A range tree on a set of points in d-dimensions is a recursively defined multi-level binary search tree. Each level of the data structure is a binary search tree on one of the d-dimensions. The first level is a binary search tree on the first of the d-coordinates. Each vertex v of this tree contains an associated structure that is a (d−1)-dimensional range tree on the last (d−1)-coordinates of the points stored in the subtree of v.

Operations

Construction

A 1-dimensional range tree on a set of n points is a binary search tree, which can be constructed in O(n log n) time. Range trees in higher dimensions are constructed recursively by constructing a balanced binary search tree on the first coordinate of the points, and then, for each vertex v in this tree, constructing a (d−1)-dimensional range tree on the points contained in the subtree of v. Constructing a range tree this way would require O(n logdn) time.

This can be improved by noticing that a range tree on a set 2-dimensional points can be constructed in O(n log n) time.[7] Let S be a set of n 2-dimensional points. If S contains only one point, return a leaf containing that point. Otherwise, construct the associated structure of S, a 1-dimensional range tree on the y-coordinates of the points in S. Let xm be the median x-coordinate of the points. Let SL be the set of points with x-coordinate less than or equal to xm and let SR be the set of points with x-coordinate greater than xm. Recursively construct vL, a 2-dimensional range tree on SL, and vR, a 2-dimensional range tree on SR. Create a vertex v with left-child vL and right-child vR. If we sort the points by their y-coordinates at the start of the algorithm, and maintain this ordering when splitting the points by their x-coordinate, we can construct the associated structures of each subtree in linear time. This reduces the time to construct a 2-dimensional range tree to O(n log n), which also reduces the time to construct a d-dimensional range tree to O(n logd−1n).

Range queries

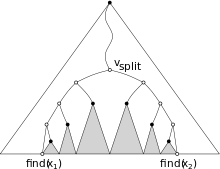
A 1-dimensional range query.
A 1-dimensional range query [x1, x2]. Points stored in the subtrees shaded in gray will be reported. find(x1) and find(x2) will be reported if they are inside the query interval.

Range trees can be used to find the set of points that lie inside a given interval. To report the points that lie in the interval [x1, x2], we start by searching for x1 and x2. At some vertex in the tree, the search paths to x1 and x2 will diverge. Let vsplit be the last vertex that these two search paths have in common. Continue searching for x1 in the range tree. For every vertex v in the search path from vsplit to x1, if the value stored at v is greater than x1, report every point in the right-subtree of v. If v is a leaf, report the value stored at v if it is inside the query interval. Similarly, reporting all of the points stored in the left-subtrees of the vertices with values less than x2 along the search path from vsplit to x2, and report the leaf of this path if it lies within the query interval.

Since the range tree is a balanced binary tree, the search paths to x1 and x2 have length O(log n). Reporting all of the points stored in the subtree of a vertex can be done in linear time using any tree traversal algorithm. It follows that the time to perform a range query is O(log n + k), where k is the number of points in the query interval.

Range queries in d-dimensions are similar. Instead of reporting all of the points stored in the subtrees of the search paths, perform a (d−1)-dimensional range query on the associated structure of each subtree. Eventually, a 1-dimensional range query will be performed and the correct points will be reported.

Similarly, 2-dimensional range queries can be done. A binary tree in the x coordinate is required, where each node is augmented with a subtree in the y coordinate containing every descendent point. Trivially this data-structure can be computed in O(nlog2n) time which can be optimized to O(nlogn). Since we are augmenting each node with a subtree, the space complexity of this data-structure is O(nlogn). Time complexity of each query would be O(log2n).


Since a d-dimensional query consists of O(log n) (d−1)-dimensional range queries, it follows that the time required to perform a d-dimensional range query is O(logdn + k), where k is the number of points in the query interval. This can be reduced to O(logd−1n + k) using the technique of fractional cascading.[2][4][7]

See also

References

  1. ↑ Bentley, J. L. (1979). "Decomposable searching problems". Information Processing Letters. 8 (5): 244–251. doi:10.1016/0020-0190(79)90117-0.
  2. 1 2 Lueker, G. S. (1978). "A data structure for orthogonal range queries". 19th Annual Symposium on Foundations of Computer Science (sfcs 1978). pp. 28–21. doi:10.1109/SFCS.1978.1.
  3. ↑ Lee, D. T.; Wong, C. K. (1980). "Quintary trees: A file structure for multidimensional database systems". ACM Transactions on Database Systems. 5 (3): 339. doi:10.1145/320613.320618.
  4. 1 2 Willard, Dan E. The super-b-tree algorithm (Technical report). Cambridge, MA: Aiken Computer Lab, Harvard University. TR-03-79.
  5. ↑ Chazelle, Bernard (1990). "Lower Bounds for Orthogonal Range Searching: I. The Reporting Case" (PDF). ACM. 37: 200–212.
  6. ↑ Chazelle, Bernard (1990). "Lower Bounds for Orthogonal Range Searching: II. The Arithmetic Model" (PDF). ACM. 37: 439–463.
  7. 1 2 de Berg, Mark; Cheong, Otfried; van Kreveld, Marc; Overmars, Mark (2008). Computational Geometry. ISBN 978-3-540-77973-5. doi:10.1007/978-3-540-77974-2.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.