Potential flow around a circular cylinder

In mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow. Unlike a real fluid, this solution indicates a net zero drag on the body, a result known as d'Alembert's paradox.

Mathematical solution^[1]

Colors: pressure field. Red is high and blue is low. Velocity vectors.

Close-up view of one quadrant of the flow. Colors: pressure field. Red is high and blue is low. Velocity vectors.

Pressure field (colors), stream function (black) with contour interval 0f

0.2Ur

from bottom to top, velocity potential (white) with contour interval

0.2Ur

from left to right.

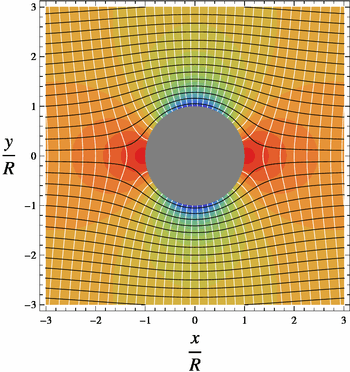
A cylinder (or disk) of radius $R$ is placed in two-dimensional, incompressible, inviscid flow. The goal is to find the steady velocity vector ${\vec {V}}$ and pressure $p$ in a plane, subject to the condition that far from the cylinder the velocity vector is

{\vec {V}}=U{\widehat {i}}+0{\widehat {j}},

where $U$ is a constant, and at the boundary of the cylinder

{\vec {V}}\cdot {\widehat {n}}=0,

where $\widehat {n}$ is the vector normal to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density $\rho$ . The flow therefore remains without vorticity, or is said to be irrotational, with $\nabla \times {\vec {V}}=0$ everywhere. Being irrotational, there must exist a velocity potential $\phi$ :

{\vec {V}}=\nabla \phi .

Being incompressible, $\nabla \cdot {\vec {V}}=0$ , so $\phi$ must satisfy Laplace's equation:

\nabla ^{2}\phi =0.

The solution for $\phi$ is obtained most easily in polar coordinates $r$ and $\theta$ , related to conventional Cartesian coordinates by $x=r\cos\theta$ and $y=r\sin \theta$ . In polar coordinates, Laplace's equation is (see Del in cylindrical and spherical coordinates):

{1 \over r}{\partial  \over \partial r}\left(r{\partial \phi  \over \partial r}\right)+{1 \over r^{2}}{\partial ^{2}\phi  \over \partial \theta ^{2}}=0

The solution that satisfies the boundary conditions is^[2] ar coordinates are obtained from the components of $\nabla \phi$ in polar coordinates:

V_{r}={\frac {\partial \phi }{\partial r}}=U\left(1-{\frac {R^{2}}{r^{2}}}\right)\cos \theta

and

V_{\theta }={\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}=-U\left(1+{\frac {R^{2}}{r^{2}}}\right)\sin \theta .

Being invisicid and irrotational, Bernoulli's equation allows the solution for pressure field to be obtained directly from the velocity field:

p={\frac {1}{2}}\rho \left(U^{2}-V^{2}\right)+p_{\infty },

where the constants $U$ and $p_{\infty }$ appear so that $p\rightarrow p_{\infty }$ far from the cylinder, where $V=U$ . Using

V^{2}=V_{r}^{2}+V_{\theta }^{2},

p={\frac {1}{2}}\rho U^{2}\left(2{\frac {R^{2}}{r^{2}}}\cos(2\theta )-{\frac {R^{4}}{r^{4}}}\right)+p_{\infty }.

In the figures, the colorized field referred to as "pressure" is a plot of

2{\frac {p-p_{\infty }}{\rho U^{2}}}=2{\frac {R^{2}}{r^{2}}}\cos(2\theta )-{\frac {R^{4}}{r^{4}}}.

On the surface of the cylinder, or $r=R$ , pressure varies from a maximum of 1 (red color) at the stagnation points at $\theta =0$ and $\theta =\pi$ to a minimum of -3 (purple) on the sides of the cylinder, at $\theta ={\tfrac {1}{2}}\pi$ and $\theta ={\tfrac {3}{2}}\pi .$ Likewise, $V$ varies from V=0 at the stagnation points to $V=2U$ on the sides, in the low pressure.

Stream function

The flow being incompressible, a stream function can be found such that

{\vec {V}}=\nabla \psi \times {\widehat {k}}.

It follows from this definition, using vector identities,

{\vec {V}}\cdot \nabla {\psi }=0.

Therefore, a contour of a constant value of $\psi$ will also be a stream line, a line tangent to ${\vec {V}}.$ For the flow past a cylinder, we find:

\psi =U\left(r-{\frac {R^{2}}{r}}\right)\sin \theta .

Physical interpretation

Laplace's equation is linear, and is one of the most elementary partial differential equations. This simple equation yields the entire solution for both ${\vec {V}}$ and $p$ because of the constraint of irrotationality and incompressibility. Having obtained the solution for ${\vec {V}}$ and $p,$ the consistency of the pressure gradient with the accelerations can be noted.

The dynamic pressure at the upstream stagnation point has value of $\rho U^{2}/2,$ a value needed to decelerate the free stream flow of speed $U.$ This same value appears at the downstream stagnation point, this high pressure is again need to decelerate the flow to zero speed. This symmetry arises only because the flow is completely frictionless.

The low pressure on sides on the cylinder is needed to provide the centripetal acceleration of the flow:

{\frac {\partial p}{\partial r}}={\frac {\rho V^{2}}{L}},

where $L$ is the radius of curvature of the flow. But $L\approx R,$ and $V\approx U.$ The integral of the equation for centripetal acceleration, which will over a distance $\Delta r\approx R$ will thus yield

p-p_{\infty }\approx -\rho U^{2}.

The exact solution has, for the lowest pressure,

p-p_{\infty }=-{\frac {3}{2}}\rho U^{2}.

The low pressure, which must be present to provide the centripetal acceleration, will also increase the flow speed as the fluid travels from higher to lower values of pressure. Thus we find the maximum speed in the flow, $V=2U,$ in the low pressure on the sides of the cylinder.

A value of $V>U$ is consistent with conservation of the volume of fluid. With the cylinder blocking some of the flow, $V$ must be greater than $U$ somewhere in the plane through the center of the cylinder and transverse to the flow.

Comparison with flow of a real fluid past a cylinder

This symmetry of this ideal solution has the peculiar property of having zero net drag on the cylinder, a property known as d'Alembert's paradox. Unlike an ideal inviscid fluid, a viscous flow past a cylinder, no matter how small the viscosity, will acquire vorticity in a thin boundary layer adjacent to the cylinder. Boundary layer separation can occur, and a trailing wake will occur behind the cylinder. The pressure will be lower on the wake side of the cylinder, than on the upstream side, resulting in a drag force in the downstream direction.

Van Dyke flows

Regular perturbation analysis for a flow around a cylinder with slight perturbation in the configurations can be found in Milton Van Dyke(1975).^[3] In the following, $\varepsilon$ will represent a small positive parameter and $a$ is the radius of the cylinder. For more detailed analyses and discussions, readers are referred to Milton Van Dyke(1975)^[4] book Pertubation Methods in Fluid Mechanics.

Slightly distorted cylinder

Here the radius of the cylinder is not $r=a$ , but a slightly distorted form $r=a(1-\varepsilon \sin ^{2}\theta )$ . Then the solution to first-order approximation is

\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon {\frac {Ur}{2}}\left[{\frac {3a^{2}}{r^{2}}}\sin \theta -{\frac {a^{4}}{r^{4}}}\sin 3\theta \right]+O(\varepsilon ^{2})

Slightly pulsating circle

Here the radius of the cylinder varies with time slightly so $r=a[1+\varepsilon f(t)]$ . Then the solution to first-order approximation is

\psi (r,\theta ,t)=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon Ur\left[{\frac {a^{2}}{r}}\theta f'(t)-{\frac {2a^{2}}{r^{2}}}f(t)\right]+O(\varepsilon ^{2})

Flow with slight vorticity

In general, the free-stream velocity $U$ is uniform, in other words $\psi =Uy$ , but here a small vorticity is imposed in the outer flow

Linear shear

Here a linear shear in the velocity is introduced.

\psi =U\left(y+{\frac {1}{2}}\varepsilon {\frac {y^{2}}{a}}\right),\ \omega =-\nabla ^{2}\psi =-\varepsilon {\frac {U}{a}}\ {\text{as}}\ x\rightarrow -\infty

where $\varepsilon$ is the small parameter. The governing equation is

\nabla ^{2}\psi =-\omega (\psi )

Then the solution to first-order approximation is

\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon {\frac {Ur}{4}}\left[{\frac {r}{a}}(1-\cos 2\theta )+{\frac {a^{3}}{r^{3}}}\cos 2\theta -{\frac {a}{r}}\right]+O(\varepsilon ^{2})

Parabolic shear

Here a parabolic shear in the outer velocity is introduced.

\psi =U\left(y+{\frac {1}{6}}\varepsilon {\frac {y^{3}}{a^{2}}}\right),\ \omega =-\nabla ^{2}\psi =-\varepsilon U{\frac {y}{a^{2}}}\ {\text{as}}\ x\rightarrow -\infty

Then the solution to first-order approximation is

\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta +\varepsilon {\frac {Ur}{6}}\left[{\frac {r^{2}}{a^{2}}}\sin ^{2}\theta -3r\ln r\sin \theta +\chi \right]+O(\varepsilon ^{2})

where $\chi$ is the homogeneous solution to the Laplace equation which restores the boundary conditions.

Slightly porous cylinder

Let $C_{ps}$ represents the surface pressure coefficient for impermeable cylinder

C_{ps}={\frac {p_{s}-p_{\infty }}{{\frac {1}{2}}\rho U^{2}}}=1-4\sin ^{2}\theta =2\cos 2\theta -1

where $p_{s}$ is the surface pressure of the impermeable cylinder and let $C_{pi}$ be the internal pressure coefficient inside the cylinder, then a slight normal velocity due to the slight porousness is given by

{\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }}=\varepsilon U(C_{pi}-C_{ps})=\varepsilon U(C_{pi}+1-2\cos 2\theta )\ {\text{at}}\ r=a

but the zero net flux condition $\int _{0}^{2\pi }{\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }}d\theta =0$ requires that $C_{pi}=-1$ . Therefore, ${\frac {\partial \psi }{\partial \theta }}=-2\varepsilon rU\cos 2\theta$ at $r=a$ . Then the solution to first-order approximation is

\psi (r,\theta )=Ur\left(1-{\frac {a^{2}}{r^{2}}}\right)\sin \theta -\varepsilon U{\frac {a^{3}}{r^{2}}}\sin 2\theta +O(\varepsilon ^{2})

Slightly compressible flow

Here the small parameter is square of the Mach number $\varepsilon =M^{2}=U^{2}/c^{2}$ where $c$ is the speed of sound. Then the solution to first-order approximation in terms of the velocity potential is

\phi (r,\theta )=Ur\left(1+{\frac {a^{2}}{r^{2}}}\right)\cos \theta -\varepsilon {\frac {Ur}{12}}\left[\left({\frac {13a^{2}}{r^{2}}}-{\frac {6a^{4}}{r^{4}}}+{\frac {a^{6}}{r^{6}}}\right)\cos \theta +\left({\frac {a^{4}}{r^{4}}}-{\frac {3a^{2}}{r^{2}}}\right)\cos 3\theta \right]+O(\varepsilon ^{2})

Corrugated quasi-cylinder

If the cylinder has variable radius in the axial direction i.e., $z$ axis, $r=a\left(1+\varepsilon \sin {\frac {z}{b}}\right)$ , then the solution to first-order approximation in terms of the three-dimensional velocity potential is

\phi (r,\theta ,z)=Ur\left(1+{\frac {a^{2}}{r^{2}}}\right)\cos \theta -2\varepsilon Ub{\frac {K_{1}(r/b)}{K_{1}'(r/b)}}\cos \theta \sin {\frac {z}{b}}+O(\varepsilon ^{2})

where $K_{1}(r/b)$ is the Modified Bessel function of the first kind of order one.

References

↑ Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.
↑ Acheson, David J. Elementary fluid dynamics. Oxford University Press, 1990.
↑ Van Dyke, Milton. Perturbation methods in fluid mechanics. Parabolic Press, Incorporated, 1975.
↑ Van Dyke, Milton. Perturbation methods in fluid mechanics. Parabolic Press, Incorporated, 1975.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.