Pfafstetter Coding System
The Pfafstetter Coding System is a hierarchical method of hydrologically coding river basins. It was developed by the Brazilian engineer Otto Pfafstetter in 1989. It is designed such that topological information is embedded in the code, which makes it easy to determine whether an event in one river basin will affect another by direct examination of their codes.[1]
History and use
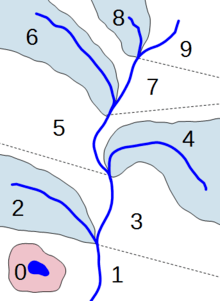
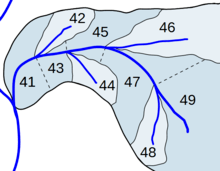
In the 1950s, Pfafstetter suggested the use of a hierarchical system of coding river basins,[2] later described in a 1989 paper.[3] The method was applied to Brazilian water networks, and has been used in a number of other applications.[4][5][6]
Description
The Pfafstetter system relies on the properties of the base-10 numbering system. In a water system to be coded, the main stem is defined as the path which drains the greatest area. The four major tributeries, in terms of water drainage, of the main stem are determined, and the water basin of each defined. This results in four tributary basins, as well as five inter-basin regions which are drained by the main stem.[1][3]
Each region is then numbered from 1-9, with the downstream-most inter-basin region denoted 1; therefore, the inter-basin regions and tributary basins are numbered 1,3,5,7,9 and 2,4,6,8 respectively. The number 0 is reserved for closed drainage systems.[1][3]
Each tributary basin is then coded in an identical manner, and the resulting number appended to the end of the tributary basin number. In this manner, the entire waterway may be coded in a recursive manner to an arbitrary precision.[1][3]
Properties
The primary advantage of the Pfafstetter system is that the water drainage topology is directly described by the code:
- At each level, higher digits denote upstream segments.
- Odd digits denote segments on the main stem; even digits denote tributaries of the main stem.
Therefore, given a point with code A on the water system, a point with code B is downstream if:[3]
- The first exactly n digits of each code match, where n ≥ 0, AND
- The remaining digits of B are:
- less than the remaining digits of A, AND
- all odd.
For example, segment 8835 is upstream of segments 8833 and 8811, but not segments 8832, 8821 or 9135.
The Pfaffstetter system is a particularly efficient system; n-digit codes can be used in a water system with 10n segments. It compares favourably in this respect to the USGS HUC method.[3]
See also
References
- 1 2 3 4 Watershed Topology - The Pfafstetter System Archived 2011-07-10 at the Wayback Machine., by Jordan Furnans and Francisco Olivera
- ↑ Jager, A. L. de; Vogt, J. V. (8 July 2010). "Development and demonstration of a structured hydrological feature coding system for Europe". Hydrological Sciences Journal. 55 (5): 661–675. ISSN 0262-6667. doi:10.1080/02626667.2010.490786.
- 1 2 3 4 5 6 Verdin, K. L; Verdin, J. P (10 May 1999). "A topological system for delineation and codification of the Earth’s river basins". Journal of Hydrology. 218 (1–2): 1–12. doi:10.1016/S0022-1694(99)00011-6.
- ↑ Jager, A. L. de; Vogt, J. V. (2010-07-08). "Development and demonstration of a structured hydrological feature coding system for Europe". Hydrological Sciences Journal. 55 (5): 661–675. ISSN 0262-6667. doi:10.1080/02626667.2010.490786.
- ↑ "HydroSHEDS". www.hydrosheds.org. Retrieved 2017-05-07.
- ↑ "HYDRO1k Documentation". webgis.wr.usgs.gov. Retrieved 2017-05-07.