Pareto efficiency

Pareto efficiency or Pareto optimality is a state of allocation of resources from which it is impossible to reallocate so as to make any one individual or preference criterion better off without making at least one individual or preference criterion worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian engineer and economist, who used the concept in his studies of economic efficiency and income distribution. The concept has been applied in academic fields such as economics, engineering, and the life sciences.

The Pareto frontier is the set of all Pareto efficient allocations, conventionally shown graphically.

A Pareto improvement is a change to a different allocation that makes at least one individual or preference criterion better off without making any other individual or preference criterion worse off, given a certain initial allocation of goods among a set of individuals. An allocation is defined as "Pareto efficient" or "Pareto optimal" when no further Pareto improvements can be made, in which case we are assumed to have reached Pareto optimality.

"Pareto efficiency" is considered as a minimal notion of efficiency that does not necessarily result in a socially desirable distribution of resources: it makes no statement about equality, or the overall well-being of a society.^[1]^[2]

The notion of Pareto efficiency has been applied to the selection of alternatives in engineering and similar fields. Each option is first assessed, under multiple criteria, and then a subset of options is ostensibly identified with the property that no other option can categorically outperform any of its members.

Overview

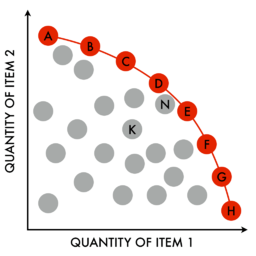
A production-possibility frontier is an example of a Pareto-efficient frontier, where the frontier and the area left and below it is a continuous room of choices. The red points are examples of Pareto-optimal choices of production. Points off the frontier, such as N and K, are not Pareto-efficient.

"Pareto optimality" is a formally defined concept used to determine when an allocation is optimal. Simply put, an allocation is not Pareto optimal if there is an alternative allocation where improvements can be made to at least one participant's well-being without reducing any other participant's well-being. If there is a transfer that satisfies this condition, the reallocation is called a "Pareto improvement." When no further Pareto improvements are possible, the allocation is a "Pareto optimum."

The formal presentation of the concept in an economy is as follows: Consider an economy with $i$ agents and $j$ goods. Then an allocation $\{x_{1},...,x_{i}\}$ , where $x_{n}\in \mathbb {R} ^{j}$ , is Pareto optimal if there is no other feasible allocation $\{x_{1}',...,x_{i}'\}$ such that, for utility function $u_{i}$ for each agent $i$ , $u_{n}(x_{n}')\geq u_{n}(x_{n})$ for all $n\in \{1,...,i\}$ with $u_{n}(x_{n}')>u_{n}(x_{n})$ for some $n$ .^[3] Here, in this simple economy, "feasibility" refers to an allocation where the total amount of each good that is allocated sums to no more than the total amount of the good in the economy. In a more complex economy with production, an allocation would consist both of consumption vectors and production vectors, and feasibility would require that the total amount of each consumed good is no greater than the initial endowment plus the amount produced.

In principle, a change from a generally inefficient economic allocation to an efficient one is not necessarily considered to be a Pareto improvement. Even when there are overall gains in the economy, if a single agent is disadvantaged by the reallocation, the allocation is not Pareto optimal. For instance, if a change in economic policy eliminates a monopoly and that market subsequently becomes competitive, the gain to others may be large. However, since the monopolist is disadvantaged, this is not a Pareto improvement. In theory, if the gains to the economy are larger than the loss to the monopolist, the monopolist could be compensated for its loss while still leaving a net gain for others in the economy, allowing for a Pareto improvement. Thus, in practice, to ensure that nobody is disadvantaged by a change aimed at achieving Pareto efficiency, compensation of one or more parties may be required. It is acknowledged, in the real world, that such compensations may have unintended consequences leading to incentive distortions over time, as agents supposedly anticipate such compensations and change their actions accordingly.^[4]

Under the idealized conditions of the first welfare theorem, a system of free markets, also called a "competitive equilibrium," leads to a Pareto-efficient outcome. It was first demonstrated mathematically by economists Kenneth Arrow and Gérard Debreu.

However, the result only holds under the restrictive assumptions necessary for the proof: markets exist for all possible goods, so there are no externalities; all markets are in full equilibrium; markets are perfectly competitive; transaction costs are negligible; and market participants have perfect information.

In the absence of perfect information or complete markets, outcomes will generally be Pareto inefficient, per the Greenwald-Stiglitz theorem.^[5]

The second welfare theorem is essentially the reverse of the first welfare-theorem. It states that under similar, ideal assumptions, any Pareto optimum can be obtained by some competitive equilibrium, or free market system, although it may also require a lump-sum transfer of wealth.^[3]

Weak Pareto efficiency

A "weak Pareto optimum" (WPO) is an allocation for which there are no possible alternative allocations whose realization would cause every individual to gain. Thus, an alternative allocation is considered to be a Pareto improvement if and only if the alternative allocation is strictly preferred by all individuals. When contrasted with weak Pareto efficiency, a standard Pareto optimum as described above may be referred to as a "strong Pareto optimum" (SPO).

Weak Pareto-optimality is "weaker" than strong Pareto-optimality in the sense that any SPO also qualifies as a WPO, but a WPO allocation is not necessarily an SPO.

A market doesn't require local nonsatiation to get to a weak Pareto-optimum.^[6]

Constrained Pareto-efficiency

The condition of constrained Pareto-optimality is a weaker version of the standard condition of Pareto optimality employed in economics, which ostensibly accounts for the fact that a potential planner (e.g., the government) may not be able to improve upon a decentralized market outcome, even if that outcome is inefficient. This will occur if it is limited by the same informational or institutional constraints as are individual agents.^[7]

The most commonly proffered example is of a setting where individuals have private information (for example, a labor market where the worker's own productivity is known to the worker but not to a potential employer, or a used-car market where the quality of a car is known to the seller but not to the buyer) which results in moral hazard or an adverse selection and a sub-optimal outcome. In such a case, a planner who wishes to improve the situation is deemed unlikely to have access to any information that the participants in the markets do not have. Hence, the planner cannot implement allocation rules which are based on the idiosyncratic characteristics of individuals; for example, "if a person is of type A, they pay price p1, but if of type B, they pay price p2" (see Lindahl prices). Essentially, only anonymous rules are allowed (of the sort "Everyone pays price p") or rules based on observable behavior; "if any person chooses x at price px then they get a subsidy of ten dollars, and nothing otherwise". If there exists no allowed rule that can successfully improve upon the market outcome, then that outcome is said to be "constrained Pareto-optimal."

Note that the concept of constrained Pareto optimality assumes benevolence on the part of the planner and hence it is distinct from the concept of government failure, which occurs when the policy making politicians fail to achieve an optimal outcome simply because they are not necessarily acting in the public's best interest.

Use in engineering and economics

Example of a Pareto frontier. The boxed points represent feasible choices, and smaller values are preferred to larger ones. Point C is not on the Pareto frontier because it is dominated by both point A and point B. Points A and B are not strictly dominated by any other, and hence do lie on the frontier.

The notion of Pareto efficiency has been used in engineering. Given a set of choices and a way of valuing them, the Pareto frontier or Pareto set or Pareto front is the set of choices that are Pareto efficient. By restricting attention to the set of choices that are Pareto-efficient, a designer can make tradeoffs within this set, rather than considering the full range of every parameter.

Formal representation

Pareto frontier

For a given system, the Pareto frontier or Pareto set is the set of parameterizations (allocations) that are all Pareto efficient. Finding Pareto frontiers is particularly useful in engineering. By yielding all of the potentially optimal solutions, a designer can make focused tradeoffs within this constrained set of parameters, rather than needing to consider the full ranges of parameters.

The Pareto frontier, P(Y), may be more formally described as follows. Consider a system with function $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$ , where X is a compact set of feasible decisions in the metric space $\mathbb {R} ^{n}$ , and Y is the feasible set of criterion vectors in $\mathbb {R} ^{m}$ , such that $Y = \{ y \in \mathbb{R}^m:\; y = f(x), x \in X\;\}$ .

We assume that the preferred directions of criteria values are known. A point $y^{\prime \prime }\in \mathbb {R} ^{m}$ is preferred to (strictly dominates) another point $y^{\prime }\in \mathbb {R} ^{m}$ , written as $y^{\prime\prime} \succ y^{\prime}$ . The Pareto frontier is thus written as:

P(Y)=\{y^{\prime }\in Y:\;\{y^{{\prime \prime }}\in Y:\;y^{{\prime \prime }}\succ y^{\prime },y^{{\prime \prime }}\neq y^{\prime }\;\}=\emptyset \}.

Relationship to the marginal rate of substitution

A significant aspect about the Pareto frontier in economics is that, at a Pareto-efficient allocation, the marginal rate of substitution is the same for all consumers. A formal statement can be derived by considering a system with m consumers and n goods, and a utility function of each consumer as $z_i=f^i(x^i)$ where $x^i=(x_1^i, x_2^i, \ldots, x_n^i)$ is the vector of goods, both for all i. The feasibility constraint is $\sum _{{i=1}}^{m}x_{j}^{i}=b_{j}$ for $j=1,\ldots ,n$ . To find the Pareto optimal allocation, we maximize the Lagrangian:

L_{i}((x_{j}^{k})_{{k,j}},(\lambda _{k})_{k},(\mu _{j})_{j})=f^{i}(x^{i})+\sum _{{k=2}}^{m}\lambda _{k}(z_{k}-f^{k}(x^{k}))+\sum _{{j=1}}^{n}\mu _{j}\left(b_{j}-\sum _{{k=1}}^{m}x_{j}^{k}\right)

where $(\lambda _{k})_{k}$ and $(\mu _{j})_{j}$ are the vectors of multipliers. Taking the partial derivative of the Lagrangian with respect to each good $x_{j}^{k}$ for $j=1,\ldots ,n$ and $k=1,\ldots ,m$ and gives the following system of first-order conditions:

{\frac {\partial L_{i}}{\partial x_{j}^{i}}}=f_{{x_{j}^{i}}}^{1}-\mu _{j}=0{\text{ for }}j=1,\ldots ,n,

{\frac {\partial L_{i}}{\partial x_{j}^{k}}}=-\lambda _{k}f_{{x_{j}^{k}}}^{i}-\mu _{j}=0{\text{ for }}k=2,\ldots ,m{\text{ and }}j=1,\ldots ,n,

where $f_{{x_{j}^{i}}}$ denotes the partial derivative of $f$ with respect to $x_{j}^{i}$ . Now, fix any $k\neq i$ and $j,s\in \{1,\ldots ,n\}$ . The above first-order condition imply that

{\frac {f_{{x_{j}^{i}}}^{i}}{f_{{x_{s}^{i}}}^{i}}}={\frac {\mu _{j}}{\mu _{s}}}={\frac {f_{{x_{j}^{k}}}^{k}}{f_{{x_{s}^{k}}}^{k}}}.

Thus, in a Pareto-optimal allocation, the marginal rate of substitution must be the same for all consumers.

Computation

Algorithms for computing the Pareto frontier of a finite set of alternatives have been studied in computer science and power engineering.^[8] They include:

"The maximum vector problem" or the skyline query.^[9]^[10]
"The scalarization algorithm" or the method of weighted sums.

Criticisms

It would be incorrect to treat Pareto efficiency as equivalent to societal optimization, as the latter is a normative concept that is a matter of interpretation that typically would account for the consequence of degrees of inequality of distribution. An example would be a school district with low property tax revenue versus one with much higher revenue. Generally, more equal distribution occurs with the help of government redistribution.

Pareto efficiency does not require a totally equitable distribution of wealth. An economy in which a wealthy few hold the vast majority of resources can be Pareto efficient. This possibility is inherent in the definition of Pareto efficiency; often the status quo is Pareto efficient regardless of the degree to which wealth is equitably distributed. A simple example is the distribution of a pie among three people. The most equitable distribution would assign one third to each person. However the assignment of, say, a half section to each of two individuals and none to the third is also Pareto optimal despite not being equitable, because none of the recipients could be made better off without decreasing someone else's share; and there are many other such distribution examples. An example of a Pareto inefficient distribution of the pie would be allocation of a quarter of the pie to each of the three, with the remainder discarded. The origin (and utility value) of the pie is conceived as immaterial in these examples. In such cases, whereby a "windfall" is gained that none of the potential distributees actually produced (e.g., land, inherited wealth, a portion of the broadcast spectrum, or some other resource), the criterion of Pareto efficiency does not determine a unique optimal allocation. Wealth consolidation may exclude others from wealth accumulation because of bars to market entry, etc.

The liberal paradox elaborated by Amartya Sen shows that when people have preferences about what other people do, the goal of Pareto efficiency can come into conflict with the goal of individual liberty.

References

↑ Barr, N. (2012). "3.2.2 The relevance of efficiency to different theories of society". Economics of the Welfare State (5th ed.). Oxford University Press. p. 46. ISBN 978-0-19-929781-8.
↑ Sen, A. (October 1993). "Markets and freedom: Achievements and limitations of the market mechanism in promoting individual freedoms" (PDF). Oxford Economic Papers. 45 (4): 519–541. JSTOR 2663703.
1 2 Mas-Colell, A.; Whinston, Michael D.; Green, Jerry R. (1995), "Chapter 16: Equilibrium and its Basic Welfare Properties", Microeconomic Theory, Oxford University Press, ISBN 0-19-510268-1
↑ See Ricardian equivalence
↑ Greenwald, B.; Stiglitz, J. E. (1986). "Externalities in economies with imperfect information and incomplete markets". Quarterly Journal of Economics. 101 (2): 229–64. JSTOR 1891114. doi:10.2307/1891114.
↑ Markey‐Towler, Brendan and John Foster. "Why economic theory has little to say about the causes and effects of inequality", School of Economics, University of Queensland, Australia, 21 Feb 2013, RePEc:qld:uq2004:476
↑ Magill, M., & Quinzii, M., Theory of Incomplete Markets, MIT Press, 2002, p. 104 .
↑ Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudria-Andreu, A.; Villafafila-Robles, R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies 2013, 6, 1439–55.
↑ Kung, H. T.; Luccio, F.; Preparata, F.P. (1975). "On finding the maxima of a set of vectors.". Journal of the ACM. 22 (4): 469–76. doi:10.1145/321906.321910.
↑ Godfrey, P.; Shipley, R.; Gryz, J. (2006). "Algorithms and Analyses for Maximal Vector Computation". VLDB Journal. 16: 5–28. doi:10.1007/s00778-006-0029-7.

Fudenberg, Drew; Tirole, Jean (1991). Game theory. Cambridge, Massachusetts: MIT Press. pp. 18–23. ISBN 9780262061414. Book preview.
Bendor, Jonathan; Mookherjee, Dilip (April 2008). "Communitarian versus Universalistic norms". Quarterly Journal of Political Science. Now Publishing Inc. 3 (1): 33–61. doi:10.1561/100.00007028.
Kanbur, Ravi (January–June 2005). "Pareto's revenge" (pdf). Journal of Social and Economic Development. Institute for Social and Economic Change, Bangalore. 7 (1): 1–11.
Ng, Yew-Kwang (2004). Welfare economics towards a more complete analysis. Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 9780333971215.
Rubinstein, Ariel; Osborne, Martin J. (1994), "Introduction", in Rubinstein, Ariel; Osborne, Martin J., A course in game theory, Cambridge, Massachusetts: MIT Press, pp. 6–7, ISBN 9780262650403 Book preview.
Mathur, Vijay K. (Spring 1991). "How well do we know Pareto optimality?". The Journal of Economic Education. Taylor and Francis via JSTOR. 22 (2): 172–178. doi:10.2307/1182422.
Newbery, David M.G.; Stiglitz, Joseph E. (January 1984). "Pareto inferior trade". Review of Economic Studies. Oxford Journals. 51 (1): 1–12. doi:10.2307/2297701.

Topics in game theory
Definitions	Normal-form game Extensive-form game Escalation of commitment Graphical game Cooperative game Succinct game Information set Hierarchy of beliefs Preference
Equilibrium concepts	Nash equilibrium Subgame perfection Mertens-stable equilibrium Bayesian Nash equilibrium Perfect Bayesian equilibrium Trembling hand Proper equilibrium Epsilon-equilibrium Correlated equilibrium Sequential equilibrium Quasi-perfect equilibrium Evolutionarily stable strategy Risk dominance Core Shapley value Pareto efficiency Gibbs equilibrium Quantal response equilibrium Self-confirming equilibrium Strong Nash equilibrium Markov perfect equilibrium
Strategies	Dominant strategies Pure strategy Mixed strategy Tit for tat Grim trigger Collusion Backward induction Forward induction Markov strategy
Classes of games	Symmetric game Perfect information Simultaneous game Sequential game Repeated game Signaling game Screening game Cheap talk Zero-sum game Mechanism design Bargaining problem Stochastic game n-player game Large Poisson game Nontransitive game Global game Strictly determined game Potential game
Games	Prisoner's dilemma Optional prisoner's dilemma Traveler's dilemma Coordination game Chicken Centipede game Volunteer's dilemma Dollar auction Battle of the sexes Stag hunt Matching pennies Ultimatum game Rock–paper–scissors Pirate game Dictator game Public goods game Blotto game War of attrition El Farol Bar problem Fair division Fair cake-cutting Cournot game Deadlock Diner's dilemma Guess 2/3 of the average Kuhn poker Nash bargaining game Prisoners and hats puzzle Trust game Princess and Monster game Rendezvous problem
Theorems	Minimax theorem Nash's theorem Purification theorem Folk theorem Revelation principle Arrow's impossibility theorem
Key figures	Albert W. Tucker Amos Tversky Ariel Rubinstein Daniel Kahneman David K. Levine David M. Kreps Donald B. Gillies Drew Fudenberg Eric Maskin Harold W. Kuhn Herbert Simon Hervé Moulin Jean Tirole Jean-François Mertens John Harsanyi John Maynard Smith Antoine Augustin Cournot John Nash John von Neumann Kenneth Arrow Kenneth Binmore Leonid Hurwicz Lloyd Shapley Melvin Dresher Merrill M. Flood Oskar Morgenstern Paul Milgrom Peyton Young Reinhard Selten Robert Axelrod Robert Aumann Robert B. Wilson Roger Myerson Samuel Bowles Thomas Schelling William Vickrey
See also	All-pay auction Alpha–beta pruning Bertrand paradox Bounded rationality Combinatorial game theory Confrontation analysis Coopetition List of game theorists List of games in game theory No-win situation Topological game Tragedy of the commons Tyranny of small decisions

Electoral systems
Part of the politics and election series
Single-winner voting system	Approval voting Borda count Bucklin voting Contingent vote Coombs' method Copeland's method Dodgson's method Exhaustive ballot First-past-the-post voting Instant-runoff voting Kemeny–Young method Majority judgment Simple majoritarianism Minimax Condorcet Nanson's method Plurality Positional voting system Range voting Ranked pairs Schulze method Two-round system
Proportional representation	Mixed-member Party-list Single transferable vote Schulze STV CPO-STV Highest averages method Sainte-Laguë D'Hondt Largest remainder method Alternative vote Plus Closed list Open list Overhang seat Underhang seat
Semi-proportional representation	Parallel voting Single non-transferable vote Cumulative voting Limited voting Proportional approval voting Sequential proportional approval voting Satisfaction approval voting
Usage	Table of voting systems by country
Voting system criteria	Condorcet criterion Condorcet loser criterion Consistency criterion Independence of clones Independence of irrelevant alternatives Independence of Smith-dominated alternatives Later-no-harm criterion Majority criterion Majority loser criterion Monotonicity criterion Mutual majority criterion Pareto efficiency Participation criterion Plurality criterion Resolvability criterion Reversal symmetry Smith criterion
Voting system quotas	Droop quota Hagenbach-Bischoff quota Hare quota Imperiali quota
Other	Ballot Election threshold First-preference votes Spoilt vote Sortition
Portal — Project

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.