Orthorhombic crystal system
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
Bravais lattices

Two-dimensional
There are two orthorhombic Bravais lattices in two dimensions: Primitive rectangular and centered rectangular. The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell.
Three-dimensional
There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.
| Bravais lattice | Primitive orthorhombic |
Base-centered orthorhombic |
Body-centered orthorhombic |
Face-centered orthorhombic |
|---|---|---|---|---|
| Pearson symbol | oP | oS | oI | oF |
| Standard unit cell | 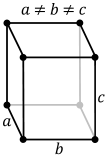 |
 |
 |
 |
| Right rhombic prism unit cell | 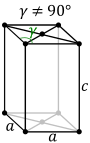 |
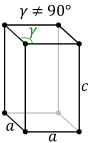 |
 |
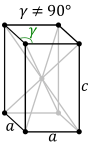 |
In the orthorhombic system there is a second choice of crystal axes that results in a unit cell with the shape of a right rhombic prism,[1] although this axis setting is very rarely used; this is because the rectangular two-dimensional base layers can also be described with rhombic axes. In this axis setting, the primitive and base-centered lattices interchange in centering type, while the same thing happens with the body-centered and face-centered lattices.
Crystal classes
The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,[2] orbifold notation, type, and space groups are listed in the table below.
| # | Point group | Type (Example) |
Space groups | ||||
|---|---|---|---|---|---|---|---|
| Name | Schön. | Intl | Orb. | Cox. | |||
| 16-24 | sphenoidal [3] | D2 | 222 | 222 | [2,2]+ | enantiomorphic (epsomite) |
P222, P2221, P21212, P212121 C2221, C222 F222 I222, I212121 |
| 25-46 | pyramidal [3] | C2v | mm2 | *22 | [2] | polar (hemimorphite, bertrandite) |
Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2 Cmm2, Cmc21, Ccc2 Amm2, Aem2, Ama2, Aea2 Fmm2, Fdd2 Imm2, Iba2, Ima2 |
| 47-74 | bipyramidal [3] | D2h | mmm | *222 | [2,2] | centrosymmetric (olivine, aragonite, marcasite) |
Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma Cmcm, Cmca, Cmmm, Cccm, Cmme, Ccce Fmmm, Fddd Immm, Ibam, Ibca, Imma |
See also
References
- ↑ See Hahn (2002), p. 746, row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90°
- ↑ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. ISBN 978-1-4020-4969-9. doi:10.1107/97809553602060000001.
- 1 2 3 "The 32 crystal classes". Retrieved 2009-07-08.
Further reading
- Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. A (5th ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-7923-6590-7. doi:10.1107/97809553602060000100.