Ontology components

Contemporary ontologies share many structural similarities, regardless of the language in which they are expressed. Most ontologies describe individuals (instances), classes (concepts), attributes, and relations.

Overview

Common components of ontologies include:

• Individuals: instances or objects (the basic or "ground level" objects)
• Classes: sets, collections, concepts, types of objects, or kinds of things.^[1]
• Attributes: aspects, properties, features, characteristics, or parameters that objects (and classes) can have
• Relations: ways in which classes and individuals can be related to one another
• Function terms: complex structures formed from certain relations that can be used in place of an individual term in a statement
• Restrictions: formally stated descriptions of what must be true in order for some assertion to be accepted as input
• Rules: statements in the form of an if-then (antecedent-consequent) sentence that describe the logical inferences that can be drawn from an assertion in a particular form
• Axioms: assertions (including rules) in a logical form that together comprise the overall theory that the ontology describes in its domain of application. This definition differs from that of "axioms" in generative grammar and formal logic. In these disciplines, axioms include only statements asserted as a priori knowledge. As used here, "axioms" also include the theory derived from axiomatic statements.
• Events: the changing of attributes or relations

Ontologies are commonly encoded using ontology languages.

Individuals

Individuals (instances) are the basic, "ground level" components of an ontology. The individuals in an ontology may include concrete objects such as people, animals, tables, automobiles, molecules, and planets, as well as abstract individuals such as numbers and words (although there are differences of opinion as to whether numbers and words are classes or individuals). Strictly speaking, an ontology need not include any individuals, but one of the general purposes of an ontology is to provide a means of classifying individuals, even if those individuals are not explicitly part of the ontology.

In formal extensional ontologies, only the utterances of words and numbers are considered individuals – the numbers and names themselves are classes. In a 4D ontology, an individual is identified by its spatio-temporal extent. Examples of formal extensional ontologies are ISO 15926 and the model in development by the IDEAS Group.

Classes

Classes – concepts that are also called type, sort, category, and kind – can be defined as an extension or an intension. According to an extensional definition, they are abstract groups, sets, or collections of objects. According to an intensional definition, they are abstract objects that are defined by values of aspects that are constraints for being member of the class. The first definition of class results in ontologies in which a class is a subclass of collection. The second definition of class results in ontologies in which collections and classes are more fundamentally different. Classes may classify individuals, other classes, or a combination of both. Some examples of classes:^[2]

• Person, the class of all people, or the abstract object that can be described by the criteria for being a person.
• Vehicle, the class of all vehicles, or the abstract object that can be described by the criteria for being a vehicle.
• Car, the class of all cars, or the abstract object that can be described by the criteria for being a car.
• Class, representing the class of all classes, or the abstract object that can be described by the criteria for being a class.
• Thing, representing the class of all things, or the abstract object that can be described by the criteria for being a thing (and not nothing).

Ontologies vary on whether classes can contain other classes, whether a class can belong to itself, whether there is a universal class (that is, a class containing everything), etc. Sometimes restrictions along these lines are made in order to avoid certain well-known paradoxes.

The classes of an ontology may be extensional or intensional in nature. A class is extensional if and only if it is characterized solely by its membership. More precisely, a class C is extensional if and only if for any class C', if C' has exactly the same members as C, then C and C' are identical. If a class does not satisfy this condition, then it is intensional. While extensional classes are more well-behaved and well understood mathematically, as well as less problematic philosophically, they do not permit the fine grained distinctions that ontologies often need to make. For example, an ontology may want to distinguish between the class of all creatures with a kidney and the class of all creatures with a heart, even if these classes happen to have exactly the same members. In most upper ontologies, the classes are defined intensionally. Intensionally defined classes usually have necessary conditions associated with membership in each class. Some classes may also have sufficient conditions, and in those cases the combination of necessary and sufficient conditions make that class a fully defined class.

Importantly, a class can subsume or be subsumed by other classes; a class subsumed by another is called a subclass (or subtype) of the subsuming class (or supertype). For example, Vehicle subsumes Car, since (necessarily) anything that is a member of the latter class is a member of the former. The subsumption relation is used to create a hierarchy of classes, typically with a maximally general class like Anything at the top, and very specific classes like 2002 Ford Explorer at the bottom. The critically important consequence of the subsumption relation is the inheritance of properties from the parent (subsuming) class to the child (subsumed) class. Thus, anything that is necessarily true of a parent class is also necessarily true of all of its subsumed child classes. In some ontologies, a class is only allowed to have one parent (single inheritance), but in most ontologies, classes are allowed to have any number of parents (multiple inheritance), and in the latter case all necessary properties of each parent are inherited by the subsumed child class. Thus a particular class of animal (HouseCat) may be a child of the class Cat and also a child of the class Pet.

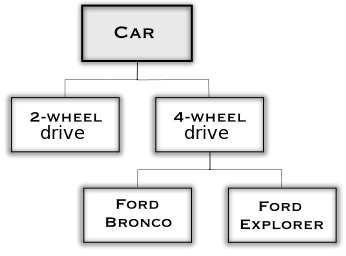
A partition is a set of related classes and associated rules that allow objects to be classified by the appropriate subclass. The rules correspond with the aspect values that distinguish the subclasses from the superclasses. For example, to the right is the partial diagram of an ontology that has a partition of the Car class into the classes 2-Wheel Drive Car and 4-Wheel Drive Car. The partition rule (or subsumption rule) determines if a particular car is classified by the 2-Wheel Drive Car or the 4-Wheel Drive Car class.

If the partition rule(s) guarantee that a single Car cannot be in both classes, then the partition is called a disjoint partition. If the partition rules ensure that every concrete object in the super-class is an instance of at least one of the partition classes, then the partition is called an exhaustive partition.

Attributes

Objects in an ontology can be described by relating them to other things, typically aspects or parts. These related things are often called attributes, although they may be independent things. Each attribute can be a class or an individual. The kind of object and the kind of attribute determine the kind of relation between them. A relation between an object and an attribute express a fact that is specific to the object to which it is related. For example the Ford Explorer object has attributes such as:

• <has as name> Ford Explorer
• <has by definition as part> door (with as minimum and maximum cardinality: 4)
• <has by definition as part one of> {4.0L engine, 4.6L engine}
• <has by definition as part> 6-speed transmission

The value of an attribute can be a complex data type; in this example, the related engine can only be one of a list of subtypes of engines, not just a single thing.

Ontologies are only true ontologies if concepts are related to other concepts (the concepts do have attributes). If that is not the case, then you would have either a taxonomy (if hyponym relationships exist between concepts) or a controlled vocabulary. These are useful, but are not considered true ontologies.

Relationships

Relationships (also known as relations) between objects in an ontology specify how objects are related to other objects. Typically a relation is of a particular type (or class) that specifies in what sense the object is related to the other object in the ontology. For example in the ontology that contains the concept Ford Explorer and the concept Ford Bronco might be related by a relation of type <is defined as a successor of>. The full expression of that fact then becomes:

• Ford Explorer is defined as a successor of : Ford Bronco

This tells us that the Explorer is the model that replaced the Bronco. This example also illustrates that the relation has a direction of expression. The inverse expression expresses the same fact, but with a reverse phrase in natural language.

Much of the power of ontologies comes from the ability to describe relations. Together, the set of relations describes the semantics of the domain. The set of used relation types (classes of relations) and their subsumption hierarchy describe the expression power of the language in which the ontology is expressed.

An important type of relation is the subsumption relation (is-a-superclass-of, the converse of is-a, is-a-subtype-of or is-a-subclass-of). This defines which objects are classified by which class. For example we have already seen that the class Ford Explorer is-a-subclass-of 4-Wheel Drive Car, which in turn is-a-subclass-of Car.

The addition of the is-a-subclass-of relationships creates a taxonomy; a tree-like structure (or, more generally, a partially ordered set) that clearly depicts how objects relate to one another. In such a structure, each object is the 'child' of a 'parent class' (Some languages restrict the is-a-subclass-of relationship to one parent for all nodes, but many do not).

Another common type of relations is the mereology relation, written as part-of, that represents how objects combine to form composite objects. For example, if we extended our example ontology to include concepts like Steering Wheel, we would say that a "Steering Wheel is-by-definition-a-part-of-a Ford Explorer" since a steering wheel is always one of the components of a Ford Explorer. If we introduce meronymy relationships to our ontology, the hierarchy that emerges is no longer able to be held in a simple tree-like structure since now members can appear under more than one parent or branch. Instead this new structure that emerges is known as a directed acyclic graph.

As well as the standard is-a-subclass-of and is-by-definition-a-part-of-a relations, ontologies often include additional types of relations that further refine the semantics they model. Ontologies might distinguish between different categories of relation types. For example:

• relation types for relations between classes
• relation types for relations between individuals
• relation types for relations between an individual and a class
• relation types for relations between a single object and a collection
• relation types for relations between collections

Relation types are sometimes domain-specific and are then used to store specific kinds of facts or to answer particular types of questions. If the definitions of the relation types are included in an ontology, then the ontology defines its own ontology definition language. An example of an ontology that defines its own relation types and distinguishes between various categories of relation types is the Gellish ontology.

For example in the domain of automobiles, we might need a made-in type relationship which tells us where each car is built. So the Ford Explorer is made-in Louisville. The ontology may also know that Louisville is-located-in Kentucky and Kentucky is-classified-as-a state and is-a-part-of the U.S.. Software using this ontology could now answer a question like "which cars are made in the U.S.?"

References