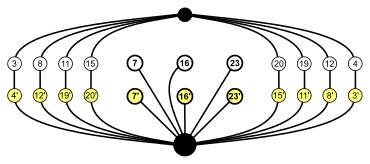
Octahedral symmetry

Point groups in three dimensions
Polyhedral group, [n,3], (*n32)
Involutional symmetry C_s, (*) [ ] =	Cyclic symmetry C_nv, (*nn) [n] =	Dihedral symmetry D_nh, (*n22) [n,2] =
Tetrahedral symmetry T_d, (*332) [3,3] =	Octahedral symmetry O_h, (*432) [4,3] =	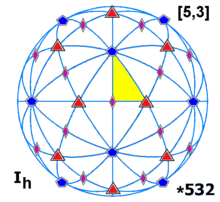Icosahedral symmetry I_h, (*532) [5,3] =

Cycle graph
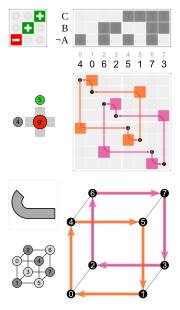
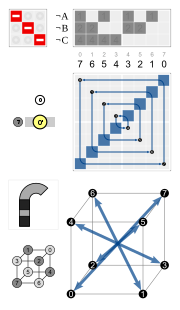
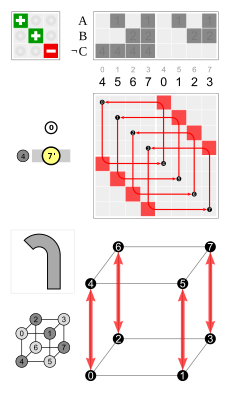
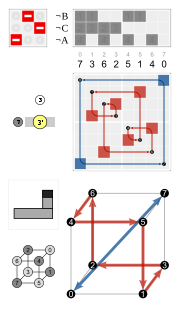
The four hexagonal cycles have the inversion (the black knot on top) in common. The hexagons are symmetric, so e.g. 3 and 4 are in the same cycle, but not 3 and 12.

A regular octahedron has 24 rotational (or orientation-preserving) symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the dual of an octahedron.

The group of orientation-preserving symmetries is S₄, the symmetric group or the group of permutations of four objects, since there is exactly one such symmetry for each permutation of the four pairs of opposite sides of the octahedron.

Details

Chiral and full (or achiral) octahedral symmetry are the discrete point symmetries (or equivalently, symmetries on the sphere) with the largest symmetry groups compatible with translational symmetry. They are among the crystallographic point groups of the cubic crystal system.

Conjugacy classes
Elements of O		Inversions of elements of O
identity	0	inversion	0'
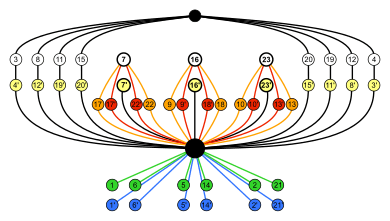
3 × rotation by 180° about a 4-fold axis	7, 16, 23	3 × reflection in a plane perpendicular to a 4-fold axis	7', 16', 23'
8 × rotation by 120° about a 3-fold axis	3, 4, 8, 11, 12, 15, 19, 20	8 × rotoreflection by 60°	3', 4', 8', 11', 12', 15', 19', 20'
6 × rotation by 180° about a 2-fold axis	1', 2', 5', 6', 14', 21'	6 × reflection in a plane perpendicular to a 2-fold axis	1, 2, 5, 6, 14, 21
6 × rotation by 90° about a 4-fold axis	9', 10', 13', 17', 18', 22'	6 × rotoreflection by 90°	9, 10, 13, 17, 18, 22

Examples
$(0,0)=0$	$(3,0)=7$	$(0,3)=3$	$(7,1)=1'$	$(4,5)=9'$
$(7,0)=0'$	$(4,0)=7'$	$(7,3)=3'$	$(0,1)=1$	$(3,5)=9$
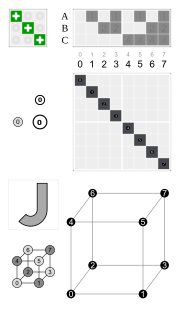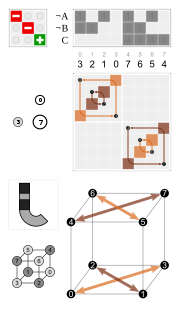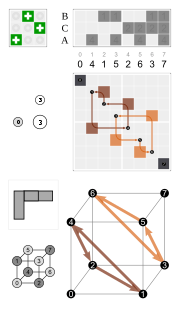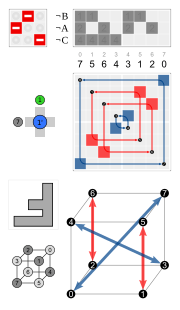A complete list can be found in the Wikiversity article.

As the hyperoctahedral group of dimension 3 the full octahedral group is the wreath product $S_{2}\wr S_{3}\simeq S_{2}^{3}\rtimes S_{3}$ ,
and a natural way to identify its elements is as pairs $(m,n)$ with $m\in [0,2^{3})$ and $n\in [0,3!)$ .
But as it is also the direct product $S_{4}\times S_{2}$ , one can simply identify the elements of tetrahedral subgrup T_d as $a\in [0,4!)$ and their inversions as $a'$ .

So e.g. the identity $(0,0)$ is represented as $0$ and the inversion $(7,0)$ as $0'$ .
$(3,1)$ is represented as $6$ and $(4,1)$ as $6'$ .

A rotoreflection is a combination of rotation and reflection.

Illustration of rotoreflections
The reflection $7'$ applied on the 120° rotation $4$ gives the 60° rotoreflection $8'$ . $7'\circ 4=8'$
The reflection $7'$ applied on the 90° rotation $22'$ gives the 90° rotoreflection $17$ . $7'\circ 22'=17$

O, 432, or [4,3]⁺ of order 24, is chiral octahedral symmetry or rotational octahedral symmetry . This group is like chiral tetrahedral symmetry T, but the C₂ axes are now C₄ axes, and additionally there are 6 C₂ axes, through the midpoints of the edges of the cube. T_d and O are isomorphic as abstract groups: they both correspond to S₄, the symmetric group on 4 objects. T_d is the union of T and the set obtained by combining each element of O \ T with inversion. O is the rotation group of the cube and the regular octahedron.

Chiral octahedral symmetry
Orthogonal projection	Stereographic projection
2-fold	4-fold	3-fold	2-fold

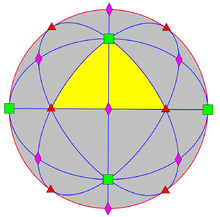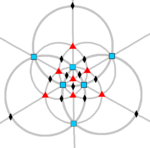O_h, *432, [4,3], or m3m of order 48 - achiral octahedral symmetry or full octahedral symmetry. This group has the same rotation axes as O, but with mirror planes, comprising both the mirror planes of T_d and T_h. This group is isomorphic to S₄.C₄, and is the full symmetry group of the cube and octahedron. It is the hyperoctahedral group for n = 3. See also the isometries of the cube.

A dual cube-octahedron.	Each face of the disdyakis dodecahedron is a fundamental domain	The octahedral group O_h with fundamental domain

With the 4-fold axes as coordinate axes, a fundamental domain of O_h is given by 0 ≤ x ≤ y ≤ z. An object with this symmetry is characterized by the part of the object in the fundamental domain, for example the cube is given by z = 1, and the octahedron by x + y + z = 1 (or the corresponding inequalities, to get the solid instead of the surface). ax + by + cz = 1 gives a polyhedron with 48 faces, e.g. the disdyakis dodecahedron.

Faces are 8-by-8 combined to larger faces for a = b = 0 (cube) and 6-by-6 for a = b = c (octahedron).

The 9 mirror lines of full octahedral symmetry can be divided into two subgroups of 3 and 6 (drawn in purple and red), representing in two orthogonal subsymmetries: D_2h, and T_d. D_2h symmetry can be doubled to D_4h by restoring 2 mirrors from one of three orientations.

Octahedral symmetry and reflective subgroups

Orthographic projection	Stereographic projection
Orthographic projection	4-fold	3-fold	2-fold
O_h, [4,3], , full octahedral symmetry (3+6 mirrors)

T_d, [3,3]=[1⁺,4,3], = , tetrahedral subgroup (6 mirrors)

C_3v, [3], , dihedral subgroup (3 mirrors)

Orthographic projection	Stereographic projection
Orthographic projection	4-fold	3-fold	2-fold
D_4h, [4,2], dihedral subgroup (1+2+2 mirrors)

D_2h, [2,2]=[4,3*], = dihedral subgroup (1+1+1 mirrors)

C_4v, [4], , dihedral subgroup (2+2 mirrors)

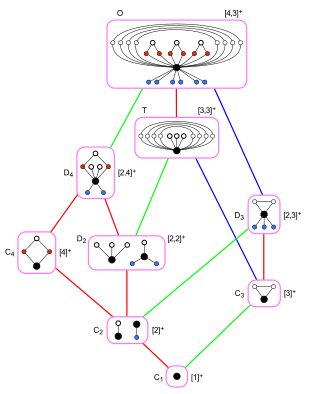
Subgroups of full octahedral symmetry

T_d

T_h

Cycle graphs of subgroups of order 24

Subgroups ordered in a Hasse diagram

Rotational subgroups

Reflective subgroups

Schoe.	Coxeter	Orb.	H-M	Structure	Order	Index
O_h	[4,3]	*432	m3m	S₄×S₂	48	1
T_d	[3,3]	*332	43m	S₄	24	2
D_4h	[2,4]	*224	4/mmm	Dih₁×Dih₄	16	3
D_2h	[2,2]	*222	mmm	Dih₁³=Dih₁×Dih₂	8	6
C_4v	[4]	*44	4mm	Dih₄	8	6
C_3v	[3]	*33	3m	Dih₃=S₃	6	8
C_2v	[2]	*22	mm2	Dih₂	4	12
C_s=C_1v	[ ]	*	2 or m	Dih₁	2	24
T_h	[3⁺,4]	3*2	m3	A₄×S₂	24	2
C_4h	[4⁺,2]	4*	4/m	Z₄×Dih₁	8	6
D_3d	[2⁺,6]	2*3	3m	Dih₆=Z₂×Dih₃	12	4
D_2d	[2⁺,4]	2*2	42m	Dih₄	8	6
C_2h = D_1d	[2⁺,2]	2*	2/m	Z₂×Dih₁	4	12
S₆	[2⁺,6⁺]	3×	3	Z₆=Z₂×Z₃	6	8
S₄	[2⁺,4⁺]	2×	8	Z₄	4	12
S₂	[2⁺,2⁺]	×	1	S₂	2	24
O	[4,3]⁺	432	432	S₄	24	2
T	[3,3]⁺	332	23	A₄	12	4
D₄	[2,4]⁺	224	422	Dih₄	8	6
D₃	[2,3]⁺	223	322	Dih₃=S₃	6	8
D₂	[2,2]⁺	222	222	Dih₂=Z₂²	4	12
C₄	[4]⁺	44	4	Z₄	4	12
C₃	[3]⁺	33	3	Z₃=A₃	3	16
C₂	[2]⁺	22	2	Z₂	2	24
C₁	[ ]⁺	11	1	Z₁	1	48

Octahedral subgroups in Coxeter notation^[1]

The isometries of the cube

48 symmetry elements of a cube

(To be integrated in the rest of the text.)

The cube has 48 isometries (symmetry elements), forming the symmetry group O_h, isomorphic to S₄ × C₂. They can be categorized as follows:

O (the identity and 23 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the body diagonals and the unit quaternion representation):
- identity (identity; 1)
- rotation about an axis from the center of a face to the center of the opposite face by an angle of 90°: 3 axes, 2 per axis, together 6 ((1 2 3 4), etc.; ((1±i)/√2, etc.)
- ditto by an angle of 180°: 3 axes, 1 per axis, together 3 ((1 2) (3 4), etc.; i,j,k)
- rotation about an axis from the center of an edge to the center of the opposite edge by an angle of 180°: 6 axes, 1 per axis, together 6 ((1 2), etc.; ((i±j)/√2, etc.)
- rotation about a body diagonal by an angle of 120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; (1±i±j±k)/2)
The same with inversion (x is mapped to −x) (also 24 isometries). Note that rotation by an angle of 180° about an axis combined with inversion is just reflection in the perpendicular plane. The combination of inversion and rotation about a body diagonal by an angle of 120° is rotation about the body diagonal by an angle of 60°, combined with reflection in the perpendicular plane (the rotation itself does not map the cube to itself; the intersection of the reflection plane with the cube is a regular hexagon).

An isometry of the cube can be identified in various ways:

by the faces three given adjacent faces (say 1, 2, and 3 on a die) are mapped to
by the image of a cube with on one face a non-symmetric marking: the face with the marking, whether it is normal or a mirror image, and the orientation
by a permutation of the four body diagonals (each of the 24 permutations is possible), combined with a toggle for inversion of the cube, or not

For cubes with colors or markings (like dice have), the symmetry group is a subgroup of O_h.

Examples:

C_4v, [4], (*422): if one face has a different color (or two opposite faces have colors different from each other and from the other four), the cube has 8 isometries, like a square has in 2D.
D_2h, [2,2], (*222): if opposite faces have the same colors, different for each set of two, the cube has 8 isometries, like a cuboid.
D_4h, [4,2], (*422): if two opposite faces have the same color, and all other faces have one different color, the cube has 16 isometries, like a square prism (square box).
C_2v, [2], (*22):
- if two adjacent faces have the same color, and all other faces have one different color, the cube has 4 isometries.
- if three faces, of which two opposite to each other, have one color and the other three one other color, the cube has 4 isometries.
- if two opposite faces have the same color, and two other opposite faces also, and the last two have different colors, the cube has 4 isometries, like a piece of blank paper with a shape with a mirror symmetry.
C_s, [ ], (*):
- if two adjacent faces have colors different from each other, and the other four have a third color, the cube has 2 isometries.
- if two opposite faces have the same color, and all other faces have different colors, the cube has 2 isometries, like an asymmetric piece of blank paper.
C_3v, [3], (*33): if three faces, of which none opposite to each other, have one color and the other three one other color, the cube has 6 isometries.

For some larger subgroups a cube with that group as symmetry group is not possible with just coloring whole faces. One has to draw some pattern on the faces.

Examples:

D_2d, [2⁺,4], (2*2): if one face has a line segment dividing the face into two equal rectangles, and the opposite has the same in perpendicular direction, the cube has 8 isometries; there is a symmetry plane and 2-fold rotational symmetry with an axis at an angle of 45° to that plane, and, as a result, there is also another symmetry plane perpendicular to the first, and another axis of 2-fold rotational symmetry perpendicular to the first.
T_h, [3⁺,4], (3*2): if each face has a line segment dividing the face into two equal rectangles, such that the line segments of adjacent faces do not meet at the edge, the cube has 24 isometries: the even permutations of the body diagonals and the same combined with inversion (x is mapped to −x).
T_d, [3,3], (*332): if the cube consists of eight smaller cubes, four white and four black, put together alternatingly in all three standard directions, the cube has again 24 isometries: this time the even permutations of the body diagonals and the inverses of the other proper rotations.
T, [3,3]⁺, (332): if each face has the same pattern with 2-fold rotational symmetry, say the letter S, such that at all edges a top of one S meets a side of the other S, the cube has 12 isometries: the even permutations of the body diagonals.

The full symmetry of the cube, O_h, [4,3], (*432), is preserved if and only if all faces have the same pattern such that the full symmetry of the square is preserved, with for the square a symmetry group, Dih₄, [4], of order 8.

The full symmetry of the cube under proper rotations, O, [4,3]⁺, (432), is preserved if and only if all faces have the same pattern with 4-fold rotational symmetry, C₄, [4]⁺.

Octahedral symmetry of the Bolza surface

In Riemann surface theory, the Bolza surface, sometimes called the Bolza curve, is obtained as the ramified double cover of the Riemann sphere, with ramification locus at the set of vertices of the regular inscribed octahedron. Its automorphism group includes the hyperelliptic involution which flips the two sheets of the cover. The quotient by the order 2 subgroup generated by the hyperelliptic involution yields precisely the group of symmetries of the octahedron. Among the many remarkable properties of the Bolza surface is the fact that it maximizes the systole among all genus 2 hyperbolic surfaces.

Solids with octahedral chiral symmetry

Class	Name	Picture	Faces	Edges	Vertices	Dual name	Picture
Archimedean solid (Catalan solid)	snub cube		38	60	24	pentagonal icositetrahedron

Solids with full octahedral symmetry

Class	Name	Faces	Edges	Vertices	Dual name
Platonic solid	Cube	6	12	8	Octahedron
Archimedean solid (dual Catalan solid)	Cuboctahedron	14	24	12	Rhombic dodecahedron
	Truncated cube	14	36	24	Triakis octahedron
	Truncated octahedron	14	36	24	Tetrakis hexahedron
	Rhombicuboctahedron	26	48	24	Deltoidal icositetrahedron
	Truncated cuboctahedron	26	72	48	Disdyakis dodecahedron
Regular compound polyhedron	Stella octangula	8	12	8	Self-dual
Regular compound polyhedron	cube and octahedron	14	24	14	Self-dual

References

↑ John Conway, The Symmetries of Things, Fig 20.8, p280

Peter R. Cromwell, Polyhedra (1997), p. 295
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
N.W. Johnson: Geometries and Transformations, (2015) Chapter 11: Finite symmetry groups

External links

Weisstein, Eric W. "Octahedral group". MathWorld.

Groupprops: Direct product of S4 and Z2

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.