Normalized Difference Vegetation Index

Negative values of NDVI (values approaching -1) correspond to water. Values close to zero (-0.1 to 0.1) generally correspond to barren areas of rock, sand, or snow. Lastly, low, positive values represent shrub and grassland (approximately 0.2 to 0.4), while high values indicate temperate and tropical rainforests (values approaching 1).[1]

The normalized difference vegetation index (NDVI) is a simple graphical indicator that can be used to analyze remote sensing measurements, typically but not necessarily from a space platform, and assess whether the target being observed contains live green vegetation or not.

Brief history

Precision Agriculture NDVI 4 cm / pixel GSD (DroneMapper)
NDVI in June over the British Isles (NOAA AVHRR)
NDVI in October over the British Isles (NOAA AVHRR)

The exploration of outer space started in earnest with the launch of Sputnik 1 by the Soviet Union on 4 October 1957. This was the first man-made satellite orbiting the Earth. Subsequent successful launches, both in the Soviet Union (e.g., the Sputnik and Cosmos programs), and in the U.S. (e.g., the Explorer program), quickly led to the design and operation of dedicated meteorological satellites. These are orbiting platforms embarking instruments specially designed to observe the Earth's atmosphere and surface with a view to improve weather forecasting. Starting in 1960, the TIROS series of satellites embarked television cameras and radiometers. This was later (1964 onwards) followed by the Nimbus satellites and the family of Advanced Very High Resolution Radiometer instruments on board the National Oceanic and Atmospheric Administration (NOAA) platforms. The latter measures the reflectance of the planet in red and near-infrared bands, as well as in the thermal infrared. In parallel, NASA developed the Earth Resources Technology Satellite (ERTS), which became the precursor to the Landsat program. These early sensors had minimal spectral resolution, but tended to include bands in the red and near-infrared, which are useful to distinguish vegetation and clouds, amongst other targets.

With the launch of the first ERTS satellite – which was soon to be renamed Landsat 1 – on July 23, 1972 with its MultiSpectral Scanner (MSS) NASA funded a number of investigations to determine its capabilities for Earth remote sensing. One of those early studies was directed toward examining the spring vegetation green-up and subsequent summer and fall dry-down (the so-called “vernal advancement and retrogradation”) throughout the north to south expanse of the Great Plains region of the central U.S. This region covered a wide range of latitudes from the southern tip of Texas to the U.S.-Canada border, which resulted in a wide range of solar zenith angles at the time of the satellite observations.

The researchers for this Great Plains study (PhD student Donald Deering and his advisor Dr. Robert Haas) found that their ability to correlate, or quantify, the biophysical characteristics of the rangeland vegetation of this region from the satellite spectral signals was confounded by these differences in solar zenith angle across this strong latitudinal gradient. With the assistance of a resident mathematician (Dr. John Schell), they studied solutions to this dilemma and subsequently developed the ratio of the difference of the red and infrared radiances over their sum as a means to adjust for or “normalize” the effects of the solar zenith angle. Originally, they called this ratio the “Vegetation Index” (and another variant, the square-root transformation of the difference-sum ratio, the “Transformed Vegetation Index”); but as several other remote sensing researchers were identifying the simple red/infrared ratio and other spectral ratios as the “vegetation index,” they eventually began to identify the difference/sum ratio formulation as the normalized difference vegetation index. The earliest reported use of NDVI in the Great Plains study was in 1973 by Rouse et al.[2] (Dr. John Rouse was the Director of the Remote Sensing Center of Texas A&M University where the Great Plains study was conducted). However, they were preceded in formulating a normalized difference spectral index by Kriegler et al. in 1969.[3] Soon after the launch of ERTS-1 (Landsat-1), Compton Tucker of NASA's Goddard Space Flight Center produced a series of early scientific journal articles describing uses of the NDVI.

Thus, NDVI was one of the most successful of many attempts to simply and quickly identify vegetated areas and their "condition," and it remains the most well-known and used index to detect live green plant canopies in multispectral remote sensing data. Once the feasibility to detect vegetation had been demonstrated, users tended to also use the NDVI to quantify the photosynthetic capacity of plant canopies. This, however, can be a rather more complex undertaking if not done properly, as is discussed below.

Rationale

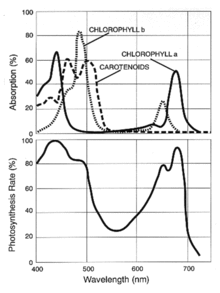
Typical PAR action spectrum, shown beside absorption spectra for chlorophyll-A, chlorophyll-B, and carotenoids

Live green plants absorb solar radiation in the photosynthetically active radiation (PAR) spectral region, which they use as a source of energy in the process of photosynthesis. Leaf cells have also evolved to re-emit solar radiation in the near-infrared spectral region (which carries approximately half of the total incoming solar energy), because the photon energy at wavelengths longer than about 700 nanometers is not large enough to synthesize organic molecules. A strong absorption at these wavelengths would only result in overheating the plant and possibly damaging the tissues. Hence, live green plants appear relatively dark in the PAR and relatively bright in the near-infrared.[4] By contrast, clouds and snow tend to be rather bright in the red (as well as other visible wavelengths) and quite dark in the near-infrared. The pigment in plant leaves, chlorophyll, strongly absorbs visible light (from 0.4 to 0.7 µm) for use in photosynthesis. The cell structure of the leaves, on the other hand, strongly reflects near-infrared light (from 0.7 to 1.1 µm). The more leaves a plant has, the more these wavelengths of light are affected, respectively. Since early instruments of Earth Observation, such as NASA's ERTS and NOAA's AVHRR, acquired data in visible and near-infrared, it was natural to exploit the strong differences in plant reflectance to determine their spatial distribution in these satellite images.

The NDVI is calculated from these individual measurements as follows:

where red and NIR stand for the spectral reflectance measurements acquired in the red (visible) and near-infrared regions, respectively (http://earthobservatory.nasa.gov/Features/MeasuringVegetation/measuring_vegetation_2.php). These spectral reflectances are themselves ratios of the reflected over the incoming radiation in each spectral band individually, hence they take on values between 0.0 and 1.0. By design, the NDVI itself thus varies between -1.0 and +1.0. It should be noted that NDVI is functionally, but not linearly, equivalent to the simple infrared/red ratio (NIR/VIS). The advantage of NDVI over a simple infrared/red ratio is therefore generally limited to any possible linearity of its functional relationship with vegetation properties (e.g. biomass). The simple ratio (unlike NDVI) is always positive, which may have practical advantages, but it also has a mathematically infinite range (0 to infinity), which can be a practical disadvantage as compared to NDVI. Also in this regard, note that the VIS term in the numerator of NDVI only scales the result, thereby creating negative values. NDVI is functionally and linearly equivalent to the ratio NIR / (NIR+VIS), which ranges from 0 to 1 and is thus never negative nor limitless in range.[5] But the most important concept in the understanding of the NDVI algebraic formula is that, despite its name, it is a transformation of a spectral ratio (NIR/VIS), and it has no functional relationship to a spectral difference (NIR-VIS).

In general, if there is much more reflected radiation in near-infrared wavelengths than in visible wavelengths, then the vegetation in that pixel is likely to be dense and may contain some type of forest. Subsequent work has shown that the NDVI is directly related to the photosynthetic capacity and hence energy absorption of plant canopies.[6][7]

Performance and limitations

It can be seen from its mathematical definition that the NDVI of an area containing a dense vegetation canopy will tend to positive values (say 0.3 to 0.8) while clouds and snow fields will be characterized by negative values of this index. Other targets on Earth visible from space include

In addition to the simplicity of the algorithm and its capacity to broadly distinguish vegetated areas from other surface types, the NDVI also has the advantage of compressing the size of the data to be manipulated by a factor 2 (or more), since it replaces the two spectral bands by a single new field (eventually coded on 8 bits instead of the 10 or more bits of the original data).

The NDVI has been widely used in applications for which it was not originally designed. Using the NDVI for quantitative assessments (as opposed to qualitative surveys as indicated above) raises a number of issues that may seriously limit the actual usefulness of this index if they are not properly addressed. The following subsections review some of these issues.

Also, the calculation of the NDVI value turns out to be sensitive to a number of perturbing factors including

For these reasons, the NDVI should be used with great caution. In any quantitative application that necessitates a given level of accuracy, all the perturbing factors that could result in errors or uncertainties of that order of magnitude should be explicitly taken into account; this may require extensive processing based on ancillary data and other sources of information. More recent versions of NDVI datasets have attempted to account for these complicating factors through processing.

A number of derivatives and alternatives to NDVI have been proposed in the scientific literature to address these limitations, including the Perpendicular Vegetation Index,[9] the Soil-Adjusted Vegetation Index,[10] the Atmospherically Resistant Vegetation Index[11] and the Global Environment Monitoring Index.[12] Each of these attempted to include intrinsic correction(s) for one or more perturbing factors. It is not until the mid-1990s, however, that a new generation of algorithms were proposed to estimate directly the biogeophysical variables of interest (e.g., the Fraction of Absorbed Photosynthetically Active Radiation or FAPAR), taking advantage of the enhanced performance and characteristics of modern sensors (in particular their multispectral and multiangular capabilities) to take all the perturbing factors into account. In spite of many possible perturbing factors upon the NDVI, it remains a valuable quantitative vegetation monitoring tool when the photosynthetic capacity of the land surface needs to be studied at the appropriate spatial scale for various phenomena.

See also

Notes

  1. ↑ http://earthobservatory.nasa.gov/Features/MeasuringVegetation/
  2. ↑ Rouse, J.W, Haas, R.H., Scheel, J.A., and Deering, D.W. (1974) 'Monitoring Vegetation Systems in the Great Plains with ERTS.' Proceedings, 3rd Earth Resource Technology Satellite (ERTS) Symposium, vol. 1, p. 48-62. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19740022592.pdf
  3. ↑ Kriegler, F.J., Malila, W.A., Nalepka, R.F., and Richardson, W. (1969) 'Preprocessing transformations and their effects on multispectral recognition.' Proceedings of the Sixth International Symposium on Remote Sensing of Environment, p. 97-131.
  4. ↑ Gates, David M. (1980) Biophysical Ecology, Springer-Verlag, New York, 611 p.
  5. ↑ Crippen, R.E. (1990) 'Calculating the vegetation index faster,' Remote Sensing of Environment, 34, 71-73.
  6. ↑ Sellers, P. J. (1985) 'Canopy reflectance, photosynthesis, and transpiration', International Journal of Remote Sensing, 6, 1335-1372.
  7. ↑ Myneni, R. B., F. G. Hall, P.J. Sellers, and A.L. Marshak (1995) 'The interpretation of spectral vegetation indexes', IEEE Transactions on Geoscience and Remote Sensing, 33, 481-486.
  8. ↑ Holben, B. N. (1986)'Characteristics of Maximum-Value Composite Images from Temporal AVHRR Data', International Journal of Remote Sensing, 7(11), 1417-1434.
  9. ↑ Richardson, A. J. and C. L. Wiegand (1977) 'Distinguishing vegetation from soil background information', Photogrammetric Engineering and Remote Sensing, 43, 1541-1552.
  10. ↑ Huete, A. R. (1988)'A soil-adjusted vegetation index (SAVI)', Remote Sensing of Environment, 25, 53-70.
  11. ↑ Kaufman, Y. J. and D. Tanre (1992) 'Atmospherically resistant vegetation index (ARVI) for EOS-MODIS', in 'Proc. IEEE Int. Geosci. and Remote Sensing Symp. '92, IEEE, New York, 261-270.
  12. ↑ Pinty, B. and M. M. Verstraete (1992) 'GEMI: A non-linear index to monitor global vegetation from satellites', Vegetatio, 101, 15-20.

References

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.