Aeolian mode

Modern Aeolian mode on A Play 

The Aeolian mode is a musical mode or, in modern usage, a diatonic scale called the natural minor scale.

History

The word Aeolian, like the names for the other ancient Greek tonoi and harmoniai, is an ethnic designation: in this case, for the inhabitants of Aeolis (Αἰολίς)—the Aeolian Islands and adjacent coastal district of Asia Minor.[1] In the music theory of ancient Greece, it was an alternative name (used by some later writers, such as Cleonides) for what Aristoxenus called the Low Lydian tonos (in the sense of a particular overall pitching of the musical system—not a scale), nine semitones higher than the lowest "position of the voice", which was called Hypodorian.[2] In the mid-16th century, this name was given by Heinrich Glarean to his newly defined ninth mode, with the diatonic octave species of the natural notes extending one octave from A to A—corresponding to the modern natural minor scale.[3] Up until this time, chant theory recognized eight musical modes: the relative natural scales in D, E, F and G, each with their authentic and plagal counterparts, and with the option of B-flat instead of B-natural in several modes.[4]

In 1547 Heinrich Glarean published his Dodecachordon. His premise had as its central idea the existence of twelve diatonic modes rather than eight, including a separate pair of modes each on the finals A and C. Finals on these notes, as well as on B♮, had been recognized in chant theory at least since Hucbald in the early tenth century, but they were regarded as merely transpositions from the regular finals a fifth lower. In the eleventh century Guido d'Arezzo, in chapter 8 of his Micrologus, designated these transposed finals A, B♮ and C as "affinals", and later still the term "confinal" was used in the same way.[5] In 1525, Pietro Aaron was the first theorist to explain polyphonic modal usage in terms of the eightfold system, including these transpositions.[6] As late as 1581, Illuminato Aiguino da Brescia published the most elaborate theory defending the eightfold system for polyphonic music against Glarean's innovations, in which he regarded the traditional plainchant modes 1 and 2 (Dorian and Hypodorian) at the affinal position (that is, with their finals on A instead of D) as a composite of species from two modes, which he described as "mixed modes".[7] Glarean added Aeolian as the name of the new ninth mode: the relative natural mode in A with the perfect fifth as its dominant, reciting note or tenor. The tenth mode, the plagal version of the Aeolian mode, Glarean called Hypoaeolian ("under Aeolian"), based on the same relative scale, but with the minor third as its tenor, and having a melodic range from a perfect fourth below the tonic to a perfect fifth above it.

Although scholars for the past three centuries have regarded the modes added by Glarean as the basis of the minor/major division of classical European music, as homophonic music replaced Renaissance polyphony, this is an oversimplification. Even the key of A minor is as closely related to the old transposed modes 1 and 2 (Dorian and Hypodorian) with finals on A—as well as to mode 3 (Phrygian)—as it is to Glarean's Aeolian.[8]

Aeolian on C  Play .

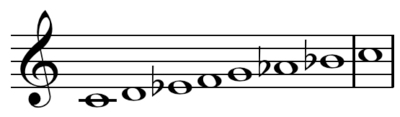
In modern usage, the Aeolian mode is the sixth mode of the major scale and has the formula 1, 2, ♭3, 4, 5, ♭6, ♭7. In C, this is C, D, E♭, F, G, A♭, B♭ (three flats); in A, this is A, B, C, D, E, F, G (no flats or sharps).

From the point of view of its relative major key, the aeolian tonic chord is the submediant minor triad (vi). For example, if the Aeolian mode is used in its all-white-note pitch based on A, this would be an A-minor triad, which would be the submediant in the relative major key of C major.

Songs that use Aeolian mode

Aeolian mode as a scale is identical with the natural minor scale. Thus, it is ubiquitous in minor-key music. The following is a list of some examples that are distinguishable from ordinary minor tonality, which also uses the melodic minor scale and the harmonic minor scale as required.

See also

References

  1. ↑ "Aeolian". Oxford English Dictionary (3rd ed.). Oxford University Press. September 2005. (Subscription or UK public library membership required.)
  2. ↑ Egert Pöhlmann, Olympia Psychopedis-Frangou, and Rudolf Maria Brandl, "Griechenland", Die Musik in Geschichte und Gegenwart: allgemeine Enzyklopädie der Musik, second, newly compiled edition, edited by Ludwig Finscher, part 1 (Sachteil), vol. 3 (Eng–Hamb) (Kassel & New York: Bärenreiter; Stuttgart: Metzler, 1995), 1652, ISBN 978-3-7618-1101-6 (Bärenreiter); ISBN 3-7618-1101-2 (Bärenreiter); ISBN 978-3-476-41000-9 (Metzler); ISBN 3-476-41000-5 (Metzler); Thomas J. Mathiesen, "Greece, §I: Ancient", The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001), 10:339. ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  3. ↑ Harold S. Powers, "Aeolian (i)", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell, 29 volumes (London: Macmillan; New York: Grove's Dictionaries, 2001), 1:. ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  4. ↑ Harold S. Powers, "Mode, §II. Medieval Modal Theory, 3: 11th-Century Syntheses, (i) Italian Theory of Modal Functions, (b) Ambitus." The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001) (Example 5). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  5. ↑ Harold S. Powers, "Mode, §II. Medieval Modal Theory, 2. Carolingian Synthesis, 9th–10th Centuries, (i) The Boethian Double Octave and the Modes, (b) Tetrachordal Degrees and Modal Quality." The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  6. ↑ Harold S. Powers, "Is Mode Real? Pietro Aron, the Octenary System, and Polyphony", Basler Jahrbuch für historische Musikpraxis 16 (1992): 9–52.
  7. ↑ Harold S. Powers, "Mode, III: Modal Theories and Polyphonic Music, 3: Polyphonic Modal Theory and the Eightfold System, (ii) Composite Modes," The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  8. ↑ Harold S. Powers, "Aeolian (i)", The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
  9. 1 2 Gary Ewer, "Dorian Mode, Aeolian Mode, Minor Key... What’s the Difference?", The Essential Secrets of Songwriting Blog (accessed 14 December 2014).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.