Nephroid
The nephroid (from the Greek ὁ νεφρός ho nephros) is a plane curve whose name means kidney-shaped (compare nephrology.) Although the term nephroid was used to describe other curves, it was applied to the curve in this article by Proctor in 1878.
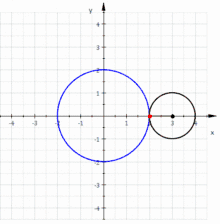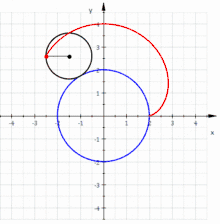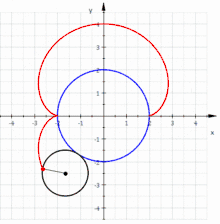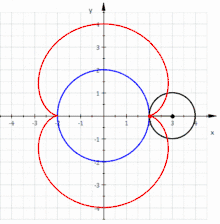
A nephroid is an algebraic curve of degree 6. It can be generated by a rolling circle with radius on the outside of a fixed circle with radius . Hence a nephroid is an epicycloid.
Equations of a nephroid
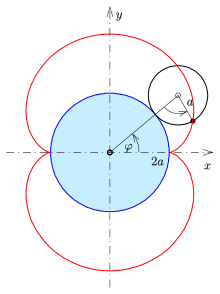
If the small circle has radius , the fixed circle has midpoint and radius , the rolling angle of the small circle is and point the starting point (s. picture) then one gets the
- parametric representation
Inserting and into the equation
shows: this equation is an implicit representation of the curve.
- proof of the parametric representation
The proof of the parametric representation is easily done by using complex numbers and their representation as complex plane. The movement of the small circle can be split into two rotations. In the complex plane a rotation of a point around point (origin) by an angle can be performed by the multiplication of point (complex number) by . Hence the
- rotation around point by angle is ,
- rotation around point by angle is .
A point of the nephroid is generated by the rotation of point by and the subsequent rotation with :
- .
Herefrom one gets
(The formulae were used. See trigonometric functions.)
- proof of the implicit representation
With
one gets
- other orientaion
If the cusps are on the y-axis the parametric representation is
and the implicit one:
Metric properties
For the nephroid above the
- arclength is
- area and
- radius of curvature is
The proofs of these statements use suitable formulae on curves (arc length, area and radius of curvature) and the parametric representation above
and their derivatives
- proof for the arc length
- .
- proof for the area
- .
- proof for the radius of curvature
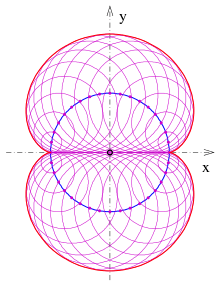
Nephroid as envelope of a pencil of circles
- Let be a circle and points of a diameter , then the envelope of the pencil of circles, which have midpoints on and are touching is a nephroid with cusps .
- proof
Let be the circle with midpoint and radius . The diameter may lie on the x-axis (s. picture). The pencil of circles has equations:
The envelope condition is
One easily checks that the point of the nephroid is a solution of the system and hence a point of the envelope of the pencil of circles.
Nephroid as envelope of a pencil of lines

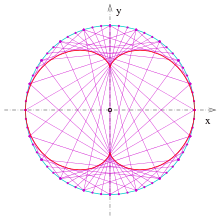
Similar to the generation of a cardioid as envelope of a pencil of lines the following procedure holds:
- Draw a circle, divide its perimeter into equal spaced parts with points (s. picture) and number them consecutively.
- Draw the chords: . (i.e.: The second point is moved by threefold velocity.)
- The envelope of these chords is a nephroid.
- proof
The following consideration uses trigonometric formulae for . In order to keep the calculations simple, the proof is given for the nephroid with cusps on the y-axis.
- equation of the tangent
- for the nephroid with parametric representation
- :
Herefrom one determines the normal vector , at first.
The equation of the tangent is:
For one gets the cusps of the nephroid, where there is no tangent. For one can divide by and yields at last
- equation of the chord
- to the circle with midpoint and radius : The equation of the chord containing the two points is:
For the chord degenerates to a point. For one can divide by and gets the equation of the chord:
The two angles are defined differently ( is one half of the rolling angle, is the parameter of the circle, whose chords are determined), for one gets the same line. Hence any chord from the circle above is tangent to the nephroid and
- the nephroid is the envelope of the chords of the circle.
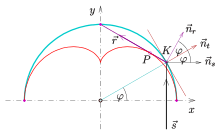
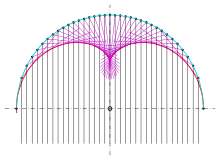
Nephroid as caustic of one half of a circle
The considerations made in the previous section give a proof for the fact, that the caustic of one half of a circle is a nephroid.
- If in the plane parallel light rays meet a reflecting half of a circle (s. picture), then the reflected rays are tangent to a nephroid.
- proof
The circle may have the origin as midpoint (as in the previous section) and its radius is . The circle has the parametric representation
The tangent at the circle point has normal vector . The reflected ray has the normal vector (s. picture) and containing circle point . Hence the reflected ray is part of the line with equation
which is tangent to the nephroid of the previous section at point
- (s. above).
The evolute and involute of a nephroid

magenta: point with osculating circle and center of curvature
evolute
The evolute of a curve is the locus of centers of curvature. In detail: For a curve with radius of curvature the evolute has the representation
with the suitably oriented unit normal.
For a nephroide one gets:
- The evolute of a nephroid is another nephroid half as large and rotated 90 degrees (s. picture).
- proof
The nephroid as shown in the picture has the parametric representation
the unit normal vector pointing to the center of curvature
- (see section above)
and the radius of curvature (s. section on metric properties). Hence the evolute has the representation:
which is a nephroid half as large and rotated 90 degrees (s. picture and section equations above)
involute
Because the evolute of a nephroid is another nephroid, so the involute of the nephroid is also another nephroid. The original nephroid in the image is the involute of the smaller nephroid.
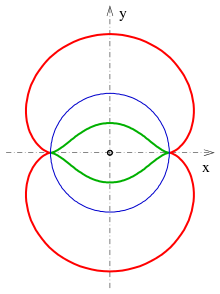
Inversion of a nephroid
The inversion
across the circle with midpoint and radius maps the nephroid with equation
onto the curve of degree 6 with equation
- (s. picture) .
References
Lockwood, E. H., A Book of Curves, Cambridge University Press, 1961.
External links
| Wikimedia Commons has media related to Nephroid. |