Molecular clock

The molecular clock is a technique that uses the mutation rate of biomolecules to deduce the time in prehistory when two or more life forms diverged. The biomolecular data used for such calculations are usually nucleotide sequences for DNA or amino acid sequences for proteins. The benchmarks for determining the mutation rate are often fossil or archaeological dates. The molecular clock was first tested in 1962 on the haemoglobin protein variants of various animals, and is commonly used in molecular evolution to estimate times of speciation or radiation. It is sometimes called a gene clock or an evolutionary clock.

Early discovery and genetic equidistance

The notion of the existence of a so-called "molecular clock" was first attributed to Émile Zuckerkandl and Linus Pauling who, in 1962, noticed that the number of amino acid differences in hemoglobin between different lineages changes roughly linearly with time, as estimated from fossil evidence.[1] They generalized this observation to assert that the rate of evolutionary change of any specified protein was approximately constant over time and over different lineages (based on the molecular clock hypothesis (MCH)).

The genetic equidistance phenomenon was first noted in 1963 by Emanuel Margoliash, who wrote: "It appears that the number of residue differences between cytochrome c of any two species is mostly conditioned by the time elapsed since the lines of evolution leading to these two species originally diverged. If this is correct, the cytochrome c of all mammals should be equally different from the cytochrome c of all birds. Since fish diverges from the main stem of vertebrate evolution earlier than either birds or mammals, the cytochrome c of both mammals and birds should be equally different from the cytochrome c of fish. Similarly, all vertebrate cytochrome c should be equally different from the yeast protein."[2] For example, the difference between the cytochrome c of a carp and a frog, turtle, chicken, rabbit, and horse is a very constant 13% to 14%. Similarly, the difference between the cytochrome c of a bacterium and yeast, wheat, moth, tuna, pigeon, and horse ranges from 64% to 69%. Together with the work of Emile Zuckerkandl and Linus Pauling, the genetic equidistance result directly led to the formal postulation of the molecular clock hypothesis in the early 1960s.[3]

Relationship with neutral theory

The observation of a clock-like rate of molecular change was originally purely phenomenological. Later, the work of Motoo Kimura[4] developed the neutral theory of molecular evolution, which predicted a molecular clock. Let there be N individuals, and to keep this calculation simple, let the individuals be haploid (i.e. have one copy of each gene). Let the rate of neutral mutations (i.e. mutations with no effect on fitness) in a new individual be . The probability that this new mutation will become fixed in the population is then 1/N, since each copy of the gene is as good as any other. Every generation, each individual can have new mutations, so there are N new neutral mutations in the population as a whole. That means that each generation, new neutral mutations will become fixed. If most changes seen during molecular evolution are neutral, then fixations in a population will accumulate at a clock-rate that is equal to the rate of neutral mutations in an individual.

Calibration

The molecular clock alone can only say that one time period is twice as long as another: it cannot assign concrete dates. For viral phylogenetics and ancient DNA studies—two areas of evolutionary biology where it is possible to sample sequences over an evolutionary timescale—the dates of the intermediate samples can be used to more precisely calibrate the molecular clock. However, most phylogenies require that the molecular clock be calibrated against independent evidence about dates, such as the fossil record.[5] There are two general methods for calibrating the molecular clock using fossil data: node calibration and tip calibration.[6]

Node calibration

Sometimes referred to as node dating, node calibration is a method for phylogeny calibration that is done by placing fossil constraints at nodes. A node calibration fossil is the oldest discovered representative of that clade, which is used to constrain its minimum age. Due to the fragmentary nature of the fossil record, the true most recent common ancestor of a clade will likely never be found.[6] In order to account for this in node calibration analyses, a maximum clade age must be estimated. Determining the maximum clade age is challenging because it relies on negative evidence—the absence of older fossils in that clade. There are a number of methods for deriving the maximum clade age using birth-death models, fossil stratigraphic distribution analyses, or taphonomic controls.[7] Alternatively, instead of a maximum and a minimum, a prior probability of the divergence time can be established and used to calibrate the clock. There are several prior probability distributions including normal, lognormal, exponential, gamma, uniform, etc.) that can be used to express the probability of the true age of divergence relative to the age of the fossil;[8] however, there are very few methods for estimating the shape and parameters of the probability distribution empirically.[9] The placement of calibration nodes on the tree informs the placement of the unconstrained nodes, giving divergence date estimates across the phylogeny. Historical methods of clock calibration could only make use of a single fossil constraint (non-parametric rate smoothing),[10] while modern analyses (BEAST[11] and r8s[12]) allow for the use of multiple fossils to calibrate the molecular clock. Simulation studies have shown that increasing the number of fossil constraints increases the accuracy of divergence time estimation.[13]

Tip calibration

Sometimes referred to as tip dating, tip calibration is a method of molecular clock calibration in which fossils are treated as taxa and placed on the tips of the tree. This is achieved by creating a matrix that includes a molecular dataset for the extant taxa along with a morphological dataset for both the extinct and the extant taxa.[7] Unlike node calibration, this method reconstructs the tree topology and places the fossils simultaneously. Molecular and morphological models work together simultaneously, allowing morphology to inform the placement of fossils.[6] Tip calibration makes use of all relevant fossil taxa during clock calibration, rather than relying on only the oldest fossil of each clade. This method does not rely on the interpretation of negative evidence to infer maximum clade ages.[7]

Total evidence dating

This approach to tip calibration goes a step further by simultaneously estimating fossil placement, topology, and the evolutionary timescale. In this method, the age of a fossil can inform its phylogenetic position in addition to morphology. By allowing all aspects of tree reconstruction to occur simultaneously, the risk of biased results is decreased.[6] This approach has been improved upon by pairing it with different models. One current method of molecular clock calibration is total evidence dating paired with the fossilized birth-death (FBD) model and a model of morphological evolution.[14] The FBD model is novel in that it allows for “sampled ancestors,” which are fossil taxa that are the direct ancestor of a living taxon or lineage. This allows fossils to be placed on a branch above an extant organism, rather than being confined to the tips.[15]

Methods

Bayesian methods can provide more appropriate estimates of divergence times, especially if large datasets—such as those yielded by phylogenomics—are employed.[16]

Non-constant rate of molecular clock

Sometimes only a single divergence date can be estimated from fossils, with all other dates inferred from that. Other sets of species have abundant fossils available, allowing the MCH of constant divergence rates to be tested. DNA sequences experiencing low levels of negative selection showed divergence rates of 0.7–0.8% per Myr in bacteria, mammals, invertebrates, and plants.[17] In the same study, genomic regions experiencing very high negative or purifying selection (encoding rRNA) were considerably slower (1% per 50 Myr).

In addition to such variation in rate with genomic position, since the early 1990s variation among taxa has proven fertile ground for research too,[18] even over comparatively short periods of evolutionary time (for example mockingbirds[19]). Tube-nosed seabirds have molecular clocks that on average run at half speed of many other birds,[20] possibly due to long generation times, and many turtles have a molecular clock running at one-eighth the speed it does in small mammals, or even slower.[21] Effects of small population size are also likely to confound molecular clock analyses. Researchers such as Francisco Ayala have more fundamentally challenged the molecular clock hypothesis.[22][23] According to Ayala's 1999 study, five factors combine to limit the application of molecular clock models:

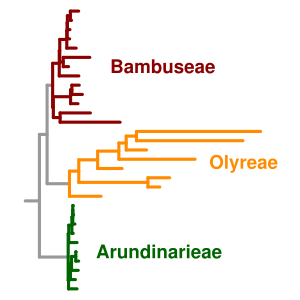
Phylogram showing three groups, one of which has strikingly longer branches than the two others
Woody bamboos (tribes Arundinarieae and Bambuseae) have long generation times and lower mutation rates, as expressed by short branches in the phylogenetic tree, than the fast-evolving herbaceous bamboos (Olyreae).

Molecular clock users have developed workaround solutions using a number of statistical approaches including maximum likelihood techniques and later Bayesian modeling. In particular, models that take into account rate variation across lineages have been proposed in order to obtain better estimates of divergence times. These models are called relaxed molecular clocks[24] because they represent an intermediate position between the 'strict' molecular clock hypothesis and Joseph Felsenstein's many-rates model[25] and are made possible through MCMC techniques that explore a weighted range of tree topologies and simultaneously estimate parameters of the chosen substitution model. It must be remembered that divergence dates inferred using a molecular clock are based on statistical inference and not on direct evidence.

The molecular clock runs into particular challenges at very short and very long timescales. At long timescales, the problem is saturation. When enough time has passed, many sites have undergone more than one change, but it is impossible to detect more than one. This means that the observed number of changes is no longer linear with time, but instead flattens out. Even at intermediate genetic distances, with phylogenetic data still sufficient to estimate topology, signal for the overall scale of the tree can be weak under complex likelihood models, leading to highly uncertain molecular clock estimates.[26]

At very short time scales, many differences between samples do not represent fixation of different sequences in the different populations. Instead, they represent alternative alleles that were both present as part of a polymorphism in the common ancestor. The inclusion of differences that have not yet become fixed leads to a potentially dramatic inflation of the apparent rate of the molecular clock at very short timescales.[27][28]

Uses

The molecular clock technique is an important tool in molecular systematics, the use of molecular genetics information to determine the correct scientific classification of organisms or to study variation in selective forces. Knowledge of approximately constant rate of molecular evolution in particular sets of lineages also facilitates establishing the dates of phylogenetic events, including those not documented by fossils, such as the divergence of living taxa and the formation of the phylogenetic tree. In these cases—especially over long stretches of time—the limitations of MCH (above) must be considered; such estimates may be off by 50% or more.

See also

References

  1. ↑ Zuckerkandl, E. and Pauling, L.B. (1962). "Molecular disease, evolution, and genic heterogeneity". In Kasha, M. and Pullman, B (editors). Horizons in Biochemistry. Academic Press, New York. pp. 189–225.
  2. ↑ Margoliash E (October 1963). "PRIMARY STRUCTURE AND EVOLUTION OF CYTOCHROME C". Proc. Natl. Acad. Sci. U.S.A. 50 (4): 672–9. Bibcode:1963PNAS...50..672M. PMC 221244 Freely accessible. PMID 14077496. doi:10.1073/pnas.50.4.672.
  3. ↑ Kumar S (August 2005). "Molecular clocks: four decades of evolution". Nat. Rev. Genet. 6 (8): 654–62. PMID 16136655. doi:10.1038/nrg1659.
  4. ↑ Kimura, Motoo (1968). "Evolutionary rate at the molecular level". Nature. 217 (5129): 624–626. Bibcode:1968Natur.217..624K. PMID 5637732. doi:10.1038/217624a0.
  5. ↑ Benton, M. J. & Donoghue, P. C. J. (2007). "Paleontological evidence to date the Tree of Life". Molecular Biology & Evolution. 24 (1): 26–53. PMID 17047029. doi:10.1093/molbev/msl150.
  6. 1 2 3 4 Donoghue, P.C.J. & Ziheng, Y. (2016). "The evolution of methods for establishing evolutionary timescales". Phil. Trans. R. Soc. B. 371 (1): 20160020. doi:10.1098/rstb.2016.0020.
  7. 1 2 3 O'Reilly, J. E. & Mario D. R. (2015). "Dating Tips for Divergence-Time Estimation". Trends in Genetics. 31 (11): 637–650. doi:10.1016/j.tig.2015.08.001.
  8. ↑ Drummond, A.; Suchard, M. A. (2012). "Bayesian phylogenetics with BEAUti and the BEAST 1.7" (PDF). Molecular Biology and Evolution. 29: 1969–1973. PMC 3408070 Freely accessible. PMID 22367748. doi:10.1093/molbev/mss075.
  9. ↑ Claramunt, S.; Cracraft, J. (2015). "A new time tree reveals Earth history’s imprint on the evolution of modern birds". Sci Adv. 1 (11): e1501005. PMC 4730849 Freely accessible. PMID 26824065. doi:10.1126/sciadv.1501005.
  10. ↑ Sanderson, M. (1997). "A nonparametric approach to estimating divergence times in the absence of rate constancy" (PDF). Molecular Biology and Evolution. 14: 1218–1231. doi:10.1093/oxfordjournals.molbev.a025731.
  11. ↑ Drummond, A.; Rambaut, A. (2007). "BEAST: Bayesian evolutionary analysis by sampling trees" (PDF). BMC Evolutionary Biology. 7: 214. doi:10.1186/1471-2148-7-214.
  12. ↑ Sanderson, M. (2003). "r8s: inferring absolute rates of molecular evolution and divergence times in the absence of a molecular clock" (PDF). Bioinformatics. 19: 301–302. doi:10.1093/bioinformatics/19.2.301.
  13. ↑ Zheng Y. & Wiens J. J. (2015). "Do missing data influence the accuracy of divergence-time estimation with BEAST?". Molecular Phylogenetics and Evolution. 85 (1): 41–49. doi:10.1016/j.ympev.2015.02.002.
  14. ↑ Heath, T. A. & Huelsenbeck, J. P. (2014). "The fossilized birth–death process for coherent calibration of divergence-time estimates". PNAS. 111 (29): E2957–E2966. doi:10.1073/pnas.1319091111.
  15. ↑ Gavryushkina, A.; Heath, T. A.; Ksepka, D. T.; Stadler, T.; Welch, D. & Drummond, A. J. (2016). "Bayesian Total-Evidence Dating Reveals the Recent Crown Radiation of Penguins". Systematic Biology (1): 1–17. doi:10.1093/sysbio/syw060.
  16. ↑ Dos Reis, M.; Inoue, J.; Hasegawa, M.; Asher, R. J.; Donoghue, P. C. J.; Yang, Z. (2012). "Phylogenomic datasets provide both precision and accuracy in estimating the timescale of placental mammal phylogeny". Proceedings of the Royal Society B: Biological Sciences. 279 (1742): 3491–3500. PMC 3396900 Freely accessible. PMID 22628470. doi:10.1098/rspb.2012.0683.
  17. ↑ Ochman H, Wilson AC (1987). "Evolution in bacteria: evidence for a universal substitution rate in cellular genomes". J Mol Evol. 26 (1–2): 74–86. PMID 3125340. doi:10.1007/BF02111283.
  18. ↑ Douzery, E.J.P., Delsuc, F., Stanhope, M.J. and Huchon, D. (2003). "Local molecular clocks in three nuclear genes: divergence times for rodents and other mammals, and incompatibility among fossil calibrations". Journal of Molecular Evolution. 57: S201–S213. PMID 15008417. doi:10.1007/s00239-003-0028-x.
  19. ↑ Hunt, J.S., Bermingham, E., and Ricklefs, R.E. (2001). "Molecular systematics and biogeography of Antillean thrashers, tremblers, and mockingbirds (Aves: Mimidae)". Auk. 118 (1): 35–55. ISSN 0004-8038. doi:10.1642/0004-8038(2001)118[0035:MSABOA]2.0.CO;2.
  20. ↑ Rheindt, F. E. & Austin, J. (2005). "Major analytical and conceptual shortcomings in a recent taxonomic revision of the Procellariiformes - A reply to Penhallurick and Wink (2004)" (PDF). Emu. 105 (2): 181–186. doi:10.1071/MU04039.
  21. ↑ Avise, J.C., Bowen, W., Lamb, T., Meylan, A.B. and Bermingham, E. (1 May 1992). "Mitochondrial DNA Evolution at a Turtle's Pace: Evidence for Low Genetic Variability and Reduced Microevolutionary Rate in the Testudines". Molecular Biology and Evolution. 9 (3): 457–473. PMID 1584014.
  22. ↑ Ayala, F.J. (1999). "Molecular clock mirages". BioEssays. 21 (1): 71–75. PMID 10070256. doi:10.1002/(SICI)1521-1878(199901)21:1<71::AID-BIES9>3.0.CO;2-B.
  23. ↑ Schwartz, J. H. & Maresca, B. (2006). "Do Molecular Clocks Run at All? A Critique of Molecular Systematics". Biological Theory. 1 (4): 357–371. doi:10.1162/biot.2006.1.4.357. Lay summary – Science Daily.
  24. ↑ Drummond, A.J., Ho, S.Y.W., Phillips, M.J. and Rambaut A. (2006). "Relaxed Phylogenetics and Dating with Confidence". PLoS Biology. 4 (5): e88. PMC 1395354 Freely accessible. PMID 16683862. doi:10.1371/journal.pbio.0040088.
  25. ↑ Felsenstein, J (2001). "Taking variation of evolutionary rates between sites into account in inferring phylogenies". J Mol Evol. 53 (4–5): 447–55. PMID 11675604. doi:10.1007/s002390010234.
  26. ↑ Marshall, D. C., et al. 2016. Inflation of molecular clock rates and dates: molecular phylogenetics, biogeography, and diversification of a global cicada radiation from Australasia (Hemiptera: Cicadidae: Cicadettini). Systematic Biology 65(1):16–34.
  27. ↑ Ho SY, Phillips MJ, Cooper A, Drummond AJ (2005). "Time dependency of molecular rate estimates and systematic overestimation of recent divergence times". Molecular Biology & Evolution. 22 (7): 1561–1568. PMID 15814826. doi:10.1093/molbev/msi145.
  28. ↑ Peterson GI, Masel J (2009). "Quantitative Prediction of Molecular Clock and Ka/Ks at Short Timescales". Molecular Biology & Evolution. 26 (11): 2595–2603. PMC 2912466 Freely accessible. PMID 19661199. doi:10.1093/molbev/msp175.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.