Meyer wavelet

Spectrum of the Meyer wavelet.

The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer.^[1] As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters,^[2] fractal random fields,^[3] and multi-fault classification.^[4]

The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function $\nu$ as:

\Psi ( \omega) := \begin{cases} \frac {1}{\sqrt{2\pi}} \sin\left(\frac {\pi}{2} \nu \left(\frac{3|\omega|}{2\pi} -1\right)\right) e^{j\omega/2} & \text{if } 2 \pi /3<|\omega|< 4 \pi /3, \\ \frac {1}{\sqrt{2\pi}} \cos\left(\frac {\pi}{2} \nu \left(\frac{3| \omega|}{4 \pi}-1\right)\right) e^{j \omega/2} & \text{if } 4 \pi /3<| \omega|< 8 \pi /3, \\ 0 & \text{otherwise}, \end{cases}

where:

\nu (x) := \begin{cases} 0 & \text{if } x < 0, \\ x & \text{if } 0< x < 1, \\ 1 & \text{if } x > 1. \end{cases}

There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts

\nu (x) := \begin{cases} {x^4}(35-84x+70{x^2}-20{x^3}) & \text{if } 0< x < 1, \\ 0 & \text{otherwise}. \end{cases}

Meyer scale function.

The Meyer scale function is given by:

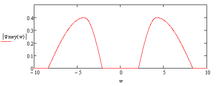
\Phi ( \omega) := \begin{cases} \frac {1}{\sqrt{2\pi}} & \text{if } | \omega|< 2 \pi /3, \\ \frac {1}{\sqrt{2\pi}} \cos\left(\frac {\pi}{2} \nu \left(\frac{3|\omega|} {2\pi}-1\right) \right) & \text{if } 2\pi/3<|\omega|< 4\pi/3, \\ 0 & \text{otherwise}. \end{cases}

In the time-domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:

Meyer wavelet.

In 2015, Victor Vermehren Valenzuela and H. M. de Oliveira gave the explicit expressions of Meyer wavelet and scale functions:^[5]

$\phi (t)=\left\{{\begin{array}{ll}{\frac {2}{3}}+{\frac {4}{3\pi }}&t=0,\\{\frac {\sin({\frac {2\pi }{3}}t)+{\frac {4}{3}}t\cos({\frac {4\pi }{3}}t)}{\pi t-{\frac {16\pi }{9}}t^{3}}}&otherwise,\end{array}}\right.$

and

$\psi (t)=\psi _{1}(t)+\psi _{2}(t)$

where

$\psi _{1}(t)={\frac {{\frac {4}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {2\pi }{3}}(t-{\frac {1}{2}})]-{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {16}{9}}(t-{\frac {1}{2}})^{3}}},$

and

$\psi _{2}(t)={\frac {{\frac {8}{3\pi }}(t-{\frac {1}{2}})\cos[{\frac {8\pi }{3}}(t-{\frac {1}{2}})]+{\frac {1}{\pi }}\sin[{\frac {4\pi }{3}}(t-{\frac {1}{2}})]}{(t-{\frac {1}{2}})-{\frac {64}{9}}(t-{\frac {1}{2}})^{3}}}.$

References

↑ Meyer, Yves (1990). Ondelettes et opérateurs: Ondelettes. Hermann. ISBN 9782705661250.
↑ Xu, L.; Zhang, D.; Wang, K. (2005). "Wavelet-based cascaded adaptive filter for removing baseline drift in pulse waveforms". IEEE Transactions on Biomedical Engineering. 52.11: 1973–1975.
↑ Elliott, Jr., F.W.; Horntrop, D.J.; Majda, A.J. (1997). "A Fourier-Wavelet Monte Carlo method for fractal random fields". Journal of Computational Physics. 132.2: 384–408.
↑ Abbasion, S.; et al. (2007). "Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine". Mechanical Systems and Signal Processing. 21.7: 2933–2945.
↑ Valenzuela, Victor Vermehren; de Oliveira, H. M. "Close expressions for Meyer Wavelet and Scale Function". p. 4.

Daubechies, Ingrid (September 1992). Ten Lectures on Wavelets (CBMS-NSF conference series in applied mathematics) (SIAM ed.). Springer-Verlag. pp. 117–119, 137–138, 152–155. ISBN 978-0-89871-274-2.

External links

Look up wavelet in Wiktionary, the free dictionary.

Wikimedia Commons has media related to Wavelet.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.