List of equations in fluid mechanics

This article summarizes equations in the theory of fluid mechanics.

Definitions

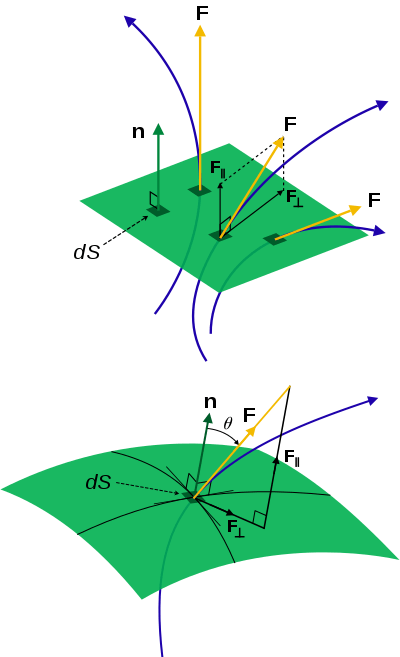
Flux F through a surface, dS is the differential vector area element, n is the unit normal to the surface. Left: No flux passes in the surface, the maximum amount flows normal to the surface. Right: The reduction in flux passing through a surface can be visualized by reduction in F or dS equivalently (resolved into components, θ is angle to normal n). F•dS is the component of flux passing though the surface, multiplied by the area of the surface (see dot product). For this reason flux represents physically a flow per unit area.

Here is a unit vector in the direction of the flow/current/flux.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Flow velocity vector field	u		m s−1	[L][T]−1
Velocity pseudovector field	ω		s−1	[T]−1
Volume velocity, volume flux	φV (no standard symbol)		m3 s−1	[L]3 [T]−1
Mass current per unit volume	s (no standard symbol)		kg m−3 s−1	[M] [L]−3 [T]−1
Mass current, mass flow rate	Im		kg s−1	[M][T]−1
Mass current density	jm		kg m−2 s−1	[M][L]−2[T]−1
Momentum current	Ip		kg m s−2	[M][L][T]−2
Momentum current density	jp		kg m s−2	[M][L][T]−2

Equations

Physical situation	Nomenclature	Equations
Fluid statics, pressure gradient	r = Position ρ = ρ(r) = Fluid density at gravitational equipotential containing r g = g(r) = Gravitational field strength at point r ∇P = Pressure gradient
Buoyancy equations	ρf = Mass density of the fluid Vimm = Immersed volume of body in fluid Fb = Buoyant force Fg = Gravitational force Wapp = Apparent weight of immersed body W = Actual weight of immersed body	Buoyant force Apparent weight
Bernoulli's equation	pconstant is the total pressure at a point on a streamline
Euler equations	ρ = fluid mass density u is the flow velocity vector E = total volume energy density U = internal energy per unit mass of fluid p = pressure denotes the tensor product
Convective acceleration
Navier–Stokes equations	TD = Deviatoric stress tensor = volume density of the body forces acting on the fluid here is the del operator.

See also

• Defining equation (physical chemistry)
• List of electromagnetism equations
• List of equations in classical mechanics
• List of equations in gravitation
• List of equations in nuclear and particle physics
• List of equations in quantum mechanics
• List of photonics equations
• List of relativistic equations
• Table of thermodynamic equations

Sources

• P.M. Whelan, M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1. 
• G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2. 
• A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN 978-0-07-025734-4. 
• R.G. Lerner, G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4. 
• C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 0-07-051400-3. 
• P.A. Tipler, G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7. 
• L.N. Hand, J.D. Finch (2008). Analytical Mechanics. Cambridge University Press,. ISBN 978-0-521-57572-0. 
• T.B. Arkill, C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray,. ISBN 0-7195-2882-8. 
• H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons,. ISBN 0-471-90182-2. 

Further reading

• L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0. 
• J.B. Marion, W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 4-8337-0195-2. 
• A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1. 
• H.D. Young, R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 0-321-50130-6. 

SI units
Authority: International System of Units (BIPM)
Base units	ampere candela kelvin kilogram metre mole second
Derived units with special names	becquerel coulomb degree Celsius farad gray henry hertz joule katal lumen lux newton ohm pascal radian siemens sievert steradian tesla volt watt weber
Other accepted units	astronomical unit bar dalton day decibel degree of arc electronvolt hectare hour litre minute minute of arc neper second of arc tonne atomic units natural units
See also	Conversion of units History of the metric system Metric prefixes Proposed redefinitions Systems of measurement
Book Category Outline