Electronic oscillator

A popular op-amp relaxation oscillator.

An electronic oscillator is an electronic circuit that produces a periodic, oscillating electronic signal, often a sine wave or a square wave.[1][2] Oscillators convert direct current (DC) from a power supply to an alternating current (AC) signal. They are widely used in many electronic devices. Common examples of signals generated by oscillators include signals broadcast by radio and television transmitters, clock signals that regulate computers and quartz clocks, and the sounds produced by electronic beepers and video games.[1]

Oscillators are often characterized by the frequency of their output signal:

Oscillators designed to produce a high-power AC output from a DC supply are usually called inverters.

There are two main types of electronic oscillator — the linear or harmonic oscillator and the nonlinear or relaxation oscillator.[2][3]

1 MHz electronic oscillator circuit which uses the resonant properties of an internal quartz crystal to control the frequency. Provides the clock signal for digital devices such as computers.

Harmonic oscillator

Block diagram of a feedback linear oscillator; an amplifier A with its output vo fed back into its input vf through a filter, β(jω).

The harmonic, or linear, oscillator produces a sinusoidal output.[2][3] There are two types:

Feedback oscillator

The most common form of linear oscillator is an electronic amplifier such as a transistor or operational amplifier connected in a feedback loop with its output fed back into its input through a frequency selective electronic filter to provide positive feedback. When the power supply to the amplifier is first switched on, electronic noise in the circuit provides a non-zero signal to get oscillations started. The noise travels around the loop and is amplified and filtered until very quickly it converges on a sine wave at a single frequency.

Feedback oscillator circuits can be classified according to the type of frequency selective filter they use in the feedback loop:[2][3]

Two common LC oscillator circuits, the Hartley and Colpitts oscillators

Negative resistance oscillator

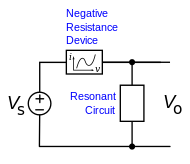
(left) Typical block diagram of a negative resistance oscillator. In some types the negative resistance device is connected in parallel with the resonant circuit. (right) A negative resistance microwave oscillator consisting of a Gunn diode in a cavity resonator. The negative resistance of the diode excites microwave oscillations in the cavity, which radiate out the aperture into a waveguide.

In addition to the feedback oscillators described above, which use two-port amplifying active elements such as transistors and operational amplifiers, linear oscillators can also be built using one-port (two terminal) devices with negative resistance,[2][3] such as magnetron tubes, tunnel diodes, lambda diodes and Gunn diodes. Negative resistance oscillators are usually used at high frequencies in the microwave range and above, since at these frequencies feedback oscillators perform poorly due to excessive phase shift in the feedback path.

In negative resistance oscillators, a resonant circuit, such as an LC circuit, crystal, or cavity resonator, is connected across a device with negative differential resistance, and a DC bias voltage is applied to supply energy. A resonant circuit by itself is "almost" an oscillator; it can store energy in the form of electronic oscillations if excited, but because it has electrical resistance and other losses the oscillations are damped and decay to zero. The negative resistance of the active device cancels the (positive) internal loss resistance in the resonator, in effect creating a resonator with no damping, which generates spontaneous continuous oscillations at its resonant frequency.

The negative resistance oscillator model is not limited to one-port devices like diodes; feedback oscillator circuits with two-port amplifying devices such as transistors and tubes also have negative resistance.[4][5][6] At high frequencies, transistors and FETs do not need a feedback loop, but with certain loads applied to one port can become unstable at the other port and show negative resistance due to internal feedback, causing them to oscillate.[4][5][7] So high frequency oscillators in general are designed using negative resistance techniques.[4][5][6]

Some of the many harmonic oscillator circuits are listed below:

Active devices used in oscillators and approximate maximum frequencies[5]
Device Frequency
Triode vacuum tube ~1 GHz
Bipolar transistor (BJT) ~20 GHz
Heterojunction Bipolar Transistor (HBT) ~50 GHz
Metal Semiconductor Field Effect Transistor (MESFET) ~100 GHz
Gunn diode, fundamental mode ~100 GHz
Magnetron tube ~100 GHz
High Electron Mobility Transistor (HEMT) ~200 GHz
Klystron tube ~200 GHz
Gunn diode, harmonic mode ~200 GHz
IMPATT diode ~300 GHz
Gyrotron tube ~300 GHz

Relaxation oscillator

A nonlinear or relaxation oscillator produces a non-sinusoidal output, such as a square, sawtooth or triangle wave.[3] It consists of an energy-storing element (a capacitor or, more rarely, an inductor) and a nonlinear switching device (a latch, Schmitt trigger, or negative resistance element) connected in a feedback loop. The switching device periodically charges and discharges the energy stored in the storage element thus causing abrupt changes in the output waveform.

Square-wave relaxation oscillators are used to provide the clock signal for sequential logic circuits such as timers and counters, although crystal oscillators are often preferred for their greater stability. Triangle wave or sawtooth oscillators are used in the timebase circuits that generate the horizontal deflection signals for cathode ray tubes in analogue oscilloscopes and television sets. They are also used in voltage controlled oscillators (VCOs), inverters and switching power supplies, dual slope analog to digital converters (ADCs), and in function generators to generate square and triangle waves for testing equipment. In general, relaxation oscillators are used at lower frequencies and have poorer frequency stability than linear oscillators.

Ring oscillators are built of a ring of active delay stages. Generally the ring has an odd number of inverting stages, so that there is no single stable state for the internal ring voltages. Instead, a single transition propagates endlessly around the ring.

Some of the more common relaxation oscillator circuits are listed below:

Voltage-controlled oscillator (VCO)

An oscillator can be designed so that the oscillation frequency can be varied over some range by an input voltage or current. These voltage controlled oscillators are widely used in phase-locked loops, in which the oscillator's frequency can be locked to the frequency of another oscillator. These are ubiquitous in modern communications circuits, used in filters, modulators, demodulators, and forming the basis of frequency synthesizer circuits which are used to tune radios and televisions.

Radio frequency VCOs are usually made by adding a varactor diode to the tuned circuit or resonator in an oscillator circuit. Changing the DC voltage across the varactor changes its capacitance, which changes the resonant frequency of the tuned circuit. Voltage controlled relaxation oscillators can be constructed by charging and discharging the energy storage capacitor with a voltage controlled current source. Increasing the input voltage increases the rate of charging the capacitor, decreasing the time between switching events.

History

Probably the first people to observe an effect due to an electrical oscillator were Auguste Arthur de la Rive, who observed a hissing arc in 1846,[8] and David Edward Hughes, who observed the humming telephone effect in 1878.[9] Although in 1880 the French engineer Jean-Marie-Anatole Gérard-Lescuyer observed oscillations in a DC powered coupled dynamo-motor system,[10] the first practical oscillators were based on electric arcs, which were used for lighting in the 19th century. Ernst Lecher in 1888 showed that the current through an electric arc could be oscillatory.[11][12][13] An oscillator was built by Elihu Thomson in 1892[14][15] by placing an LC tuned circuit in parallel with an electric arc and included a magnetic blowout. Independently, in the same year, George Francis Fitzgerald realized that if the damping resistance in a resonant circuit could be made zero or negative, the circuit would produce oscillations, and, unsuccessfully, tried to build a negative resistance oscillator with a dynamo, what would now be called a parametric oscillator.[16][17] The arc oscillator was rediscovered and popularized by William Duddell in 1900.[18][19] The current through an arc light is unstable and often produces hissing, humming or howling sounds.[17] Duddell, a student at London Technical College, investigated this effect. He attached an LC circuit to the electrodes of an arc lamp, and the LC circuit tuned the frequency of the sound.[17] Some of the energy was radiated as sound waves by the arc, producing a musical tone. Duddell demonstrated his oscillator before the London Institute of Electrical Engineers by sequentially connecting different tuned circuits across the arc to play the national anthem "God Save the Queen".[17] Duddell's "singing arc" did not generate frequencies above the audio range. In 1902 Danish physicists Valdemar Poulsen and P. O. Pederson were able to increase the frequency produced into the radio range, inventing the Poulsen arc radio transmitter, the first continuous wave radio transmitter, which was used through the 1920s.[20][21][22]

A 120 MHz oscillator from 1938 using a parallel rod transmission line resonator (Lecher line). Transmission lines are widely used for UHF oscillators.

The vacuum tube feedback oscillator was invented around 1912, when it was discovered that feedback ("regeneration") in the recently invented audion vacuum tube could produce oscillations. At least six researchers independently made this discovery and can be said to have some role in the invention.[23][24] In the summer of 1912, Edwin Armstrong observed oscillations in audion radio receiver circuits[25] and went on to use positive feedback in his invention of the regenerative receiver.[26][27] German Alexander Meissner independently discovered positive feedback and invented oscillators in March 1913.[25][28] Irving Langmuir at General Electric observed feedback in 1913.[28] Fritz Lowenstein may have preceded the others with a crude oscillator in late 1911.[29] In Britain, H. J. Round patented amplifying and oscillating circuits in 1913.[25] In August 1912, Lee De Forest, the inventor of the audion, had also observed oscillations in his amplifiers, but he didn't understand its significance and tried to eliminate it[30][31] until he read Armstrong's patents in 1914,[32] which he promptly challenged.[33] Armstrong and De Forest fought a protracted legal battle over the rights to the "regenerative" oscillator circuit[33][34] which has been called "the most complicated patent litigation in the history of radio".[35] De Forest ultimately won before the Supreme Court in 1934 on technical grounds, but most sources regard Armstrong's claim as the stronger one.[31][33]

The first and most widely used relaxation oscillator circuit, the astable multivibrator, was invented in 1917 by French engineers Henri Abraham and Eugene Bloch.[36][37][38] They called their cross-coupled, dual vacuum tube circuit a multivibrateur, because the square-wave signal it produced was rich in harmonics,[37][38] compared to the sinusoidal signal of other vacuum tube oscillators.

Vacuum tube feedback oscillators became the basis of radio transmission by 1920. However, the triode vacuum tube oscillator performed poorly above 300 MHz because of interelectrode capacitance. To reach higher frequencies, new "transit time" (velocity modulation) vacuum tubes were developed, in which electrons traveled in "bunches" through the tube. The first of these was the Barkhausen-Kurz oscillator (1920), the first tube to produce power in the UHF range. The most important and widely used were the klystron (R. and S. Varian, 1937) and the cavity magnetron (J. Randall and H. Boot, 1940).

Mathematical conditions for feedback oscillations, now called the Barkhausen criterion, were derived by Heinrich Georg Barkhausen in 1921. The first analysis of a nonlinear electronic oscillator model, the Van der Pol oscillator, was done by Balthasar van der Pol in 1927.[39] He showed that the stability of the oscillations (limit cycles) in actual oscillators was due to the nonlinearity of the amplifying device. He originated the term "relaxation oscillation" and was first to distinguish between linear and relaxation oscillators. Further advances in mathematical analysis of oscillation were made by Hendrik Wade Bode and Harry Nyquist[40] in the 1930s. In 1969 K. Kurokawa derived necessary and sufficient conditions for oscillation in negative resistance circuits,[41] which form the basis of modern microwave oscillator design.[7]

See also

References

  1. 1 2 Snelgrove, Martin (2011). "Oscillator". McGraw-Hill Encyclopedia of Science and Technology, 10th Ed., Science Access online service. McGraw-Hill. Retrieved March 1, 2012.
  2. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Chattopadhyay, D. (2006). Electronics (fundamentals And Applications). New Age International. pp. 224–225. ISBN 81-224-1780-9.
  3. 1 2 3 4 5 6 7 8 Garg, Rakesh Kumar; Ashish Dixit; Pavan Yadav (2008). Basic Electronics. Firewall Media. p. 280. ISBN 8131803023.
  4. 1 2 3 Kung, Fabian Wai Lee (2009). "Lesson 9: Oscillator Design" (PDF). RF/Microwave Circuit Design. Prof. Kung's website, Multimedia University. Retrieved October 17, 2012., Sec. 3 Negative Resistance Oscillators, p. 9-10, 14
  5. 1 2 3 4 Räisänen, Antti V.; Arto Lehto (2003). Radio Engineering for Wireless Communication and Sensor Applications. USA: Artech House. pp. 180–182. ISBN 1580535429.
  6. 1 2 Ellinger, Frank (2008). Radio Frequency Integrated Circuits and Technologies, 2nd Ed. USA: Springer. pp. 391–394. ISBN 3540693246.
  7. 1 2 Maas, Stephen A. (2003). Nonlinear Microwave and RF Circuits, 2nd Ed. Artech House. pp. 542–544. ISBN 1580534848.
  8. ↑ https://archive.org/details/wirelesstelephon00ruhmrich
  9. ↑ https://link.springer.com/article/10.1007/BF00611436
  10. ↑ Letellier, Christopher (2013). Chaos in Nature. World Scientific. p. 103. ISBN 9814374423.
  11. ↑ Anders, André (2009). Cathodic Arcs: From Fractal Spots to Energetic Condensation. Springer Science and Business Media. pp. 31–32. ISBN 0387791086.
  12. ↑ Cady, W. G.; Arnold, H. D. (1907). "On the electric arc between metallic electrodes". American Journal of Science. Tuttle, Morehouse, and Taylor Co. 24 (143): 406. Retrieved April 12, 2017.
  13. ↑ "Notes". The Electrical Review. 62 (1578): 812. February 21, 1908. Retrieved April 12, 2017.
  14. ↑ Morse 1925, p. 23
  15. ↑ US 500630, Thomson, Elihu, "Method of and Means for Producing Alternating Currents", published 18 July 1892, issued 4 July 1893
  16. ↑ G. Fitzgerald, On the Driving of Electromagnetic Vibrations by Electromagnetic and Electrostatic Engines, read at the January 22, 1892 meeting of the Physical Society of London, in Larmor, Joseph, ed. (1902). The Scientific Writings of the late George Francis Fitzgerald. London: Longmans, Green and Co. pp. 277–281.
  17. 1 2 3 4 Hong, Sungook (2001). Wireless: From Marconi's Black-Box to the Audion. MIT Press. ISBN 0262082985., pp. 161–165
  18. ↑ Morse 1925, pp. 80–81
  19. ↑ GB 190021629, Duddell, William du Bois, "Improvements in and connected with Means for the Conversion of Electrical Energy, Derived from a Source of Direct Current, into Varying or Alternating Currents", published 29 Nov 1900, issued 23 Nov 1901
  20. ↑ Morse 1925, p. 31
  21. ↑ GB 190315599, Poulsen, Valdemar, "Improvements relating to the Production of Alternating Electric Currents", issued 14 July 1904
  22. ↑ US 789449, Poulsen, Valdemar, "Method of Producing Alternating Currents with a High Number of Vibrations", issued 9 May 1905
  23. ↑ Hempstead, Colin; William E. Worthington (2005). Encyclopedia of 20th-Century Technology. 2. Taylor & Francis. p. 648. ISBN 1579584640.
  24. ↑ Hong 2001, p. 156
  25. 1 2 3 Fleming, John Ambrose (1919). The Thermionic Valve and its Developments in Radiotelegraphy and Telephony. London: The Wireless Press. pp. 148–155.
  26. ↑ Hong, Sungook (2003). "A history of the regeneration circuit: From invention to patent litigation" (PDF). IEEE. Retrieved August 29, 2012., pp. 9–10
  27. ↑ Armstrong, Edwin H. (September 1915). "Some recent developments in the Audion receiver" (PDF). Proc. of the IRE. New York: Institute of Radio Engineers. 3 (9): 215–247. doi:10.1109/jrproc.1915.216677. Retrieved August 29, 2012.
  28. 1 2 Hong 2003, p. 13
  29. ↑ Hong 2003, p. 5
  30. ↑ Hong 2003, pp. 6–7
  31. 1 2 Hijiya, James A. (1992). Lee De Forest and the Fatherhood of Radio. Lehigh University Press. pp. 89–90. ISBN 0934223238.
  32. ↑ Hong 2003, p. 14
  33. 1 2 3 Nahin, Paul J. (2001). The Science of Radio: With Matlab and Electronics Workbench Demonstration, 2nd Ed. Springer. p. 280. ISBN 0387951504.
  34. ↑ Hong 2001, pp. 181–189
  35. ↑ Hong 2003, p. 2
  36. ↑ Abraham, H.; E. Bloch (1919). "Measurement of period of high frequency oscillations". Comptes Rendus. French Academy of Sciences. 168: 1105.
  37. 1 2 Glazebrook, Richard (1922). A Dictionary of Applied Physics, Vol. 2: Electricity. London: Macmillan and Co. Ltd. pp. 633–634.
  38. 1 2 Calvert, James B. (2002). "The Eccles-Jordan Circuit and Multivibrators". Dr. J. B. Calvert website, Univ. of Denver. Retrieved May 15, 2013. External link in |publisher= (help)
  39. ↑ Van der Pol, Balthazar (1927). "On relaxation-oscillations". The London, Edinburgh and Dublin Philosophical Magazine. 2 (7): 978–992. doi:10.1080/14786442608564127.
  40. ↑ Nyquist, H. (January 1932). "Regeneration Theory" (PDF). Bell System Tech. J. USA: American Tel. & Tel. 11 (1): 126–147. doi:10.1002/j.1538-7305.1932.tb02344.x. Retrieved December 5, 2012. on Alcatel-Lucent website
  41. ↑ Kurokawa, K. (July 1969). "Some Basic Characteristics of Broadband Negative Resistance Oscillator Circuits" (PDF). Bell System Tech. J. USA: American Tel. & Tel. 48 (6): 1937–1955. doi:10.1002/j.1538-7305.1969.tb01158.x. Retrieved December 8, 2012. Eq. 10 is a necessary condition for oscillation; eq. 12 is a sufficient condition,

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.