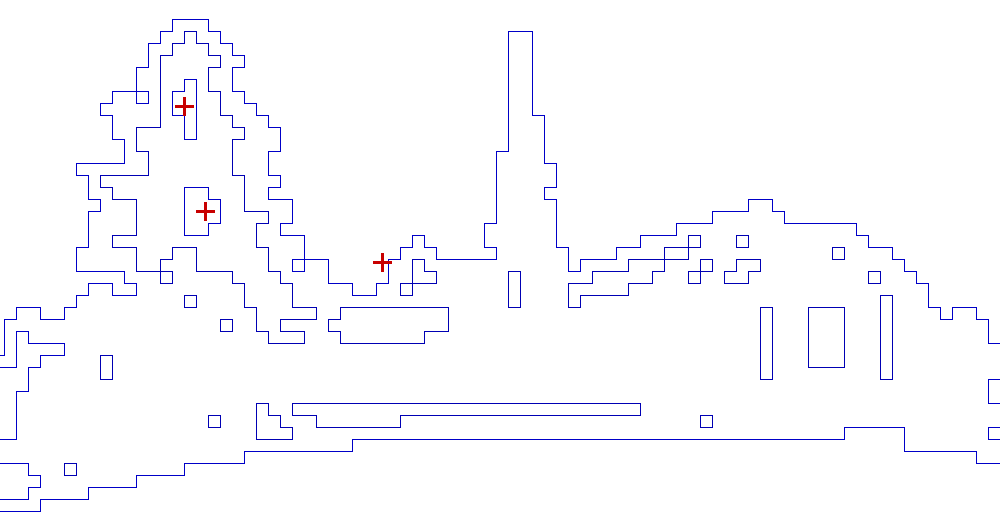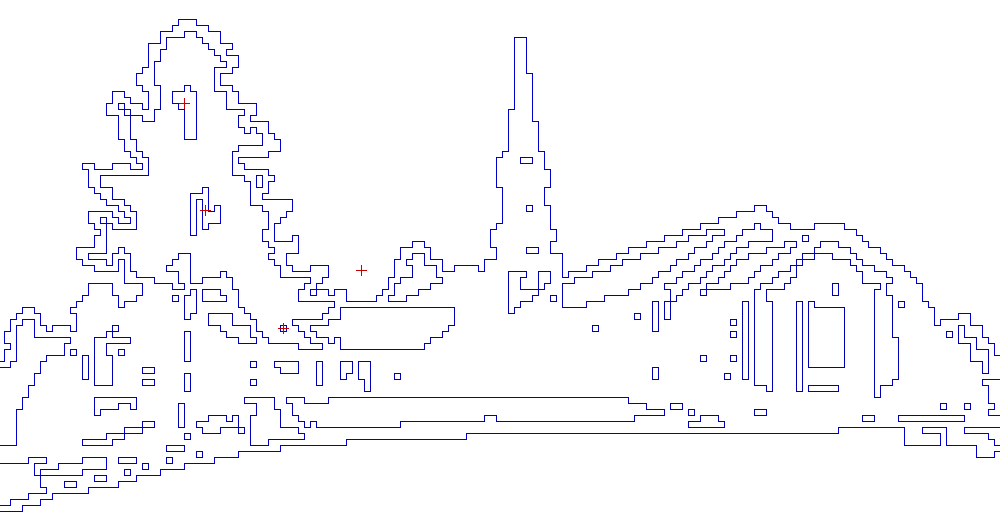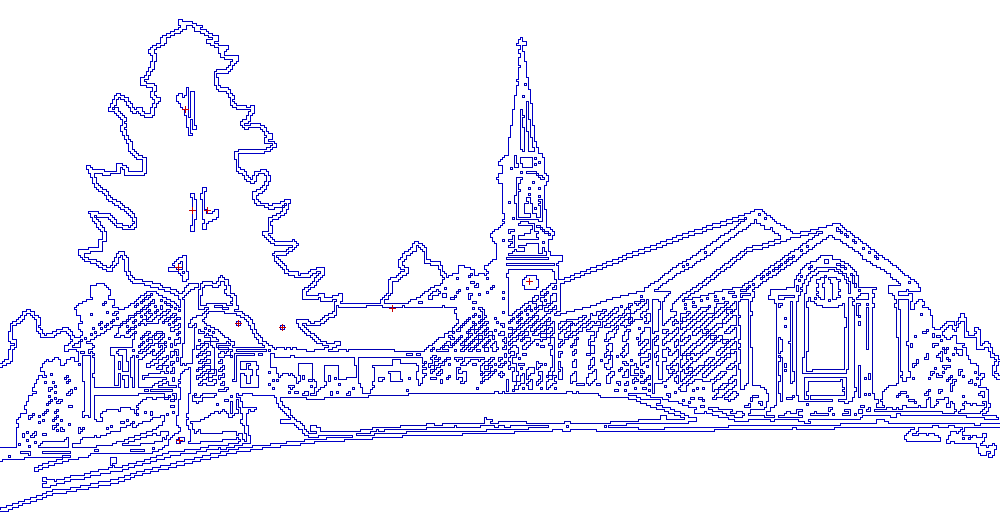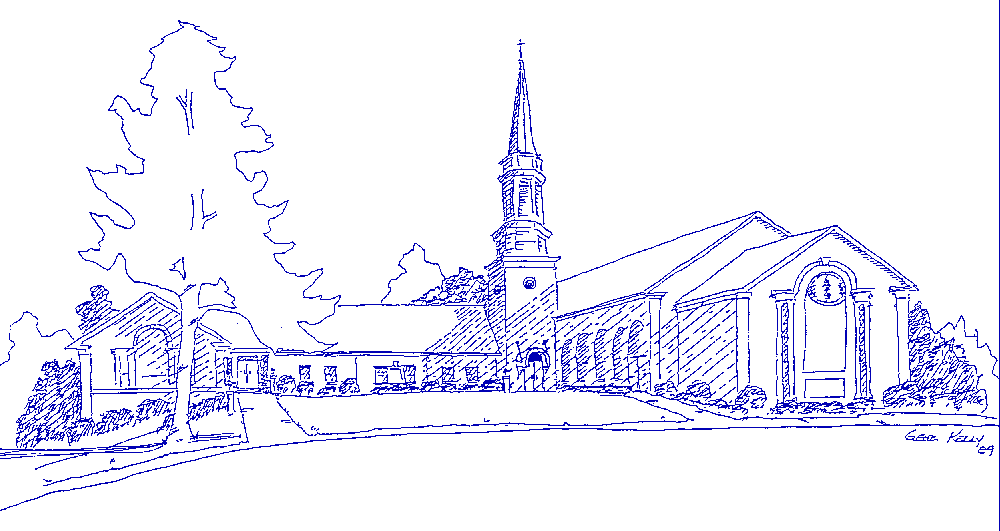
Isothetic polygon

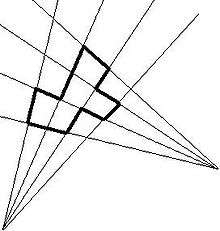
An isothetic polygon

An isothetic polygon is a polygon whose alternate sides belong to two parametric families of straight lines which are pencils of lines with centers at two points (possibly the point at infinity). The most well-known example of isothetic polygons are rectilinear polygons, and the former term is commonly used as a synonym for the latter one.

Etymology and history

The term is produced from Greek roots: iso- for "equal, same, similar" and thetos (position, placement), i,e., the term is supposed to mean "polygon with similarly placed sides".

The term was suggested during the early years of the computational geometry. Much emphasis was placed on the development of efficient algorithms for operations with orthogonal polygons, since the latter ones had an important application: representation of shapes in integrated circuit mask layouts due to their simplicity for design and manufacturing. It was observed that the efficiency of many geometric algorithms for orthogonal polygons does not really depend on the fact that their sides meet at right angles, but rather on the fact that their sides are naturally split into two alternating sets (of vertical and horizontal segments).

Sets of isothetic polygons

In many applications of computational geometry, when a problem is stated for a set of rectilinear polygons, it is very often implicitly assumed that these polygons have the same alignment (in fact, aligned to the same orthogonal coordinate axes), and hence the term "isothetic polygons" would be less ambiguous. In the context of digital geometry, isothetic polygons are practically axis-parallel and have integer coordinates of their vertices.

Examples of isothetic polygons
Example of a set of isothetic polygons that acts as a set of minimum-area covers of an object in the digital plane for changing grid sizes.

References

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.