Inversion in a sphere

Inversion of a cylinder passing through the sphere.

In geometry, inversion in a sphere is a transformation of Euclidean space that fixes the points of a sphere while sending the points inside of the sphere to the outside of the sphere, and vice versa. Intuitively, it "swaps the inside and outside" of the sphere while leaving the points on the sphere unchanged. Inversion is a conformal transformation, and is the basic operation of inversive geometry.

Definition

Inversion in a sphere is most easily described using polar coordinates. Choose a system of affine coordinates so that the centre of the sphere is at the origin and the radius of the sphere is 1. Then every point can be written in the form rv, where r is the distance from the point to the origin and v is a unit vector; moreover, for every point apart from the origin this representation is unique. Given such a representation of a point, its image under spherical inversion is defined to be the point r⁻¹v. This defines a homeomorphism from $\mathbb {R} ^{n}\setminus \{0\}$ to itself. As a map from Euclidean space to itself, the spherical inversion map is not defined at the origin, but we can extend it to ${\overline {\mathbb {R} ^{n}}}$ , the one-point compactification of $\mathbb {R} ^{n}$ , by specifying that 0 should be sent to infinity and infinity should be sent to 0. Thus, spherical inversion can be thought of as a homeomorphism of ${\overline {\mathbb {R} ^{n}}}$ .

Properties

Inversion is self-inverse, and fixes the points lying on the sphere. The inverse of a line is a circle through the centre of the reference sphere, and vice versa. The inverse of a plane is a sphere through the centre of the reference sphere, and vice versa. Otherwise the inverse of a circle is a circle; the inverse of a sphere is a sphere.

Inversion in a sphere is a powerful transformation. One simple example is in map projection.

The usual projection of the North or South Pole is inversion from the Earth to a plane. If instead of making a pole the centre, we chose a city, then Inversion could produce a map where all the shortest routes (great circles) for flying from that city would appear as straight lines, which would simplify the flight path, for passengers at least.

Proofs

Let the reference sphere be Σ, with centre O and radius r denoted by {O, r}. All inverses, in this paper, are in the sphere Σ.

The results in this article are dependent on three simple ideas:

1. Similar triangles: A scale model is the same shape as the original, i.e. all angles are kept.

2. The angle in a semicircle is a right angle. i.e. For any point on a semicircle, the diagonal makes a right angle (90^o).

3. The angles of a triangle add up to 180^o, so an external angle equals the sum of the other two internal angles.

Definition

Let P be a point at distance n > 0 from O.
If P' be a point on OP, on the same direction as OP, such that OP.OP' = r², then P, and P' are inverse points
If n > r, then OP' < r, so P' lies inside Σ, and vice versa.
Points on the surface of Σ are the only self-inverse points.

Construction

As in inversion in a circle, the usual construction, for a point, P, outside the sphere, is to take any plane through OP,
draw tangents, in the plane, from P to Σ, meeting it at S, T.
The intersection of the chord ST with OP gives P'. (Triangles OPS, OSP' are similar.)
For a point P inside Σ, take a plane through OP, draw a chord of the sphere in that plane, normal to OP at P, meeting Σ, at S, T.
Draw tangents, in the plane, to meet at P', the inverse of P.
In either case, The right angled triangles, OPT, OTP' are similar, so OP/OT = OT/OP'

(See fig 1)

Fig 1

Inversion of a pair of points

Given two points A, B with inverses A', B'; OA'.OA = r², OB'.OB = r².
So OA'/OB' = OB/OA.
Since ∠AOB is ∠B'OA', the triangles AOB, B'OA' are similar.
So ∠OAB = ∠OB'A', ∠OBA = ∠OA'B'.

(See fig 2)

Fig 2

Inverse of a line

If the line intersects Σ, then only the two points of intersection are self-inverse.
If O lies on the line, then the line is self inverse;

Else,

Let P be the foot of the perpendicular from O to the line, with inverse P', and let X be any point on the line, with inverse X',
By 'Inversion of a pair of points', ∠OX'P' = ∠OPX = 90^o.
So X' lies on a circle through O, with OP' as diameter. (Angle in a semicircle is a right angle)

(See fig 3)

Fig 3

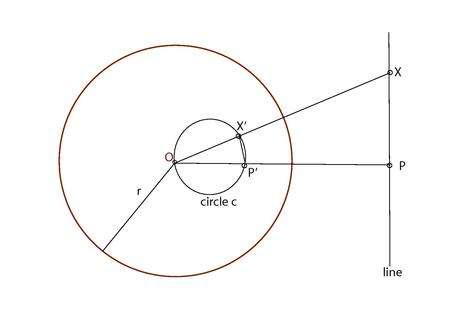
Note 4: Generally, the inverse of a line is a circle through the centre of reference.

Inverse of a plane

If the plane intersects Σ, then each point of the circle of intersection is self-inverse.
If O lies on the plane, the inverse is the plane;
Else:

Let the foot of the perpendicular from O to the plane be P with inverse P'.
Let X be any point on the plane with inverse X'.
By 'Inversion of a pair of points', ∠OX'P' = ∠OPX = 90^o.
X' lies on a sphere with diameter OP'.(angle in a semicircle is a rightangle)

Note 5: Generally, the inverse of a plane is a sphere through the centre of reference.

Inverse of a Sphere

Let the sphere be {A, a}, i.e. centre A and radius a > 0.
If sphere{A, a} intersects Σ, the only self-inverse points are on the circle of intersection.
If A is at O then the inverse of sphere{A, a} is a concentric sphere with radius r²/a;

(Trivially, if a = r, then every point on {A, a} is self-inverse.)

Else

if O lies on sphere{A, a},
Then let P be a point diametrically opposite O on sphere{A, a}, with P' the inverse of P.
Let X be any point on sphere{A, a}, with X' as inverse.
Then by 'Inversion of a pair of points' ∠OP'X' = ∠OXP = 90^o (angle in a semicircle).
This is true for all points on sphere{A, a}.
So X' lies on a plane through P' normal to OP'.

Else,

Let S, T be the intersections of OA and sphere{A, a}, with S', T' their inverses.
ST is a diameter of {A, a}.
Let X be any point on sphere{A, a}, with inverse X'.
∠OXT = ∠OT'X', and ∠OXS = ∠OS'X'. (inverse of a pair of points)

If T, S lie on the same side of O.

∠T'X'S' = ∠OX'S' − ∠OX'T'
= ∠OSX − ∠OTX (Inversion of a pair of points).
= ∠TXS (external angle equals sum of internal angles)
= 90^o (angle in a semicircle is a right angle)
So X' lies on a semicircle, with T'S' as diameter.
This is true for every point on sphere {A, a}.
So X' lies on a sphere, with T'S' as diameter.

(See fig 4)

Fig 4

If T, S lie on opposite sides of O:

∠OXT + ∠OXS = 90^o (angle in a semi-circle is a rightangle).
∠T'X'S' = ∠OX'T' + ∠OX'S'
= ∠OTX + ∠OSX (inverse of a pair of points).
= 180^o − ∠TXS (angles in a triangle sum to 180^o)
So ∠T'X'S' = 90^o, and X' lies on a semicircle, with T'S' as diameter (angle in a semicircle is a rightangle).
As before:
This is true for every point on sphere {A, a}.
So X' lies on a sphere, with T'S' as diameter.

(See fig 5)

Fig 5

Note 6: Generally the inverse of a sphere is a sphere
(The only exception is when the centre of the reference sphere lies on the sphere.)

Inverse of a circle

Let the circle be c, with centre C and radius a, lying on a plane ψ .
If c intersects the sphere, the only self-inverse points are those two intersections.
Let S, T be the nearest and furthest points of c, from O, (i.e. OT > OS), with T', S' their inverses,
If C is at O then the inverse of c is a concentric circle with radius r²/a;

Else

if O lies on c,
Then let OP be a diameter of c, with P' the inverse of P.
Let X be any point of the circle, with inverse X'.
By 'Inversion of a pair of points', ∠OP'X' = ∠OXP = 90^o.
The inverse of points of the circle lie on a line in the plane of c, normal to OP';

Else

If O lies in the plane of c, then c is a great circle of sphere {C, a}, in a plane through O, S, T, so arguments that applied to inverse of a sphere also apply to the inverse of circle c, with similar results to all those of Section 6.

(Cf Figs 3, 4, 5)

Else,

in the general case, where O is not on ψ,the plane of c;
Let A, B be two points on a line through C, perpendicular to ψ.
Let Λ, Ω, be two spheres through c, with centres A, B, neither through O.
Let a spheres, Λ', Ω', be the inverses of Λ, Ω (see Note 6).
Every point of the inverse of c lies on both Λ' and Ω'.
The intersection of the spheres Λ', Ω' is a circle c', say, the inverse of c.

If O lis on the line AB, the cone of projection is right circular,

and If c lies on sphere Σ, then every point of c is self-inverse;

Note 7: Generally the inverse of a circle is a circle.

(The only exception is when the centre of the reference sphere lies on the circle.

Results of inversion in a sphere

A line through the centre of inversion is self-inverse.
Generally, the inverse of a line is a circle through the centre of inversion.
The inverse of a circle through the centre of inversion is a line.
Generally the inverse of a circle is a circle.
A plane through the centre of inversion is self-inverse.
Generally, the inverse of a plane is a sphere through the centre of inversion.
The inverse of a sphere through the centre of inversion is a plane.
Generally the inverse of a sphere is a sphere.

References

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Inversion in a sphere

Definition

Properties

Proofs

Definition

Construction

Inversion of a pair of points

Inverse of a line

Inverse of a plane

Inverse of a Sphere

Inverse of a circle

Results of inversion in a sphere

See also

References