Homoclinic bifurcation
In mathematics, a homoclinic bifurcation is a global bifurcation which often occurs when a periodic orbit collides with a saddle point.
The image below shows a phase portrait before, at, and after a homoclinic bifurcation in 2D. The periodic orbit grows until it collides with the saddle point. At the bifurcation point the period of the periodic orbit has grown to infinity and it has become a homoclinic orbit. After the bifurcation there is no longer a periodic orbit.
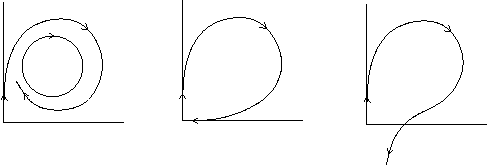
Homoclinic bifurcations can occur supercritically or subcritically. The variant above is the "small" or "type I" homoclinic bifurcation. In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic dynamics.
Literature
- Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos. Addison-Wesley. p. 262. ISBN 0-201-54344-3.