Hexagonal bipyramid
| Hexagonal bipyramid | |
|---|---|
 | |
| Type | bipyramid |
| Faces | 12 triangles |
| Edges | 18 |
| Vertices | 8 |
| Schläfli symbol | { } + {6} |
| Coxeter diagram |
|
| Symmetry group | D6h, [6,2], (*226), order 24 |
| Rotation group | D6, [6,2]+, (226), order 12 |
| Dual polyhedron | hexagonal prism |
| Face configuration | V4.4.6 |
| Properties | convex, face-transitive |
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.
Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have six faces, and because its faces cannot be equilateral triangles.
It is one of an infinite set of bipyramids. Having twelve faces, it is a type of dodecahedron, although that name is usually associated with the regular polyhedral form with pentagonal faces. The term dodecadeltahedron is sometimes used to distinguish the bipyramid from the Platonic solid, although in chemistry this term more often refers to the snub disphenoid.
The hexagonal bipyramid has a plane of symmetry (which is horizontal in the figure to the right) where the bases of the two pyramids are joined. This plane is a regular hexagon. There are also six planes of symmetry crossing through the two apices. These planes are rhombic and lie at 30° angles to each other, perpendicular to the horizontal plane.
Images
It can be drawn as a tiling on a sphere which also represents the fundamental domains of [3,2], *322 dihedral symmetry:
Related polyhedra
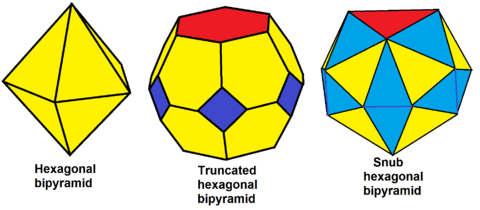
The hexagonal bipyramid, dt{2,6}, can be in sequence truncated, tdt{2,6} and alternated (snubbed), sdt{2,6}:
The hexagonal bipyramid, dt{2,6}, can be in sequence rectified, rdt{2,6}, truncated, trdt{2,6} and alternated (snubbed), srdt{2,6}:
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |
|
 |
 |
 |
|
 |
 |
 | ||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Duals to uniforms | ||||||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
It the first polyhedra in a sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
| *n32 symmetry mutations of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| Polyhedron |  |
 |
 |
 |
 |
 | |||
|---|---|---|---|---|---|---|---|---|---|
| Coxeter | |||||||||
| Tiling |  |
 |
 |
 |
 |
 |
 | ||
| Config. | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
See also
- hexagonal trapezohedron A similar 12-sided polyhedron with a twist and kite faces.
- Snub disphenoid Another 12-sided polyhedron with 2-fold symmetry and only triangular faces.
External links
- Weisstein, Eric Wolfgang. "Dipyramid". MathWorld.
- Olshevsky, George. "Bipyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML model hexagonal dipyramid
- Conway Notation for Polyhedra Try: dP6