Point groups in four dimensions

A hierarchy of 4D polychoric point groups and some subgroups. Vertical positioning is grouped by order. Blue, green, and pink colors show reflectional, hybrid, and rotational groups.

Some 4D point groups in Conway's notation

In geometry, a point group in four dimensions is an isometry group in four dimensions that leaves the origin fixed, or correspondingly, an isometry group of a 3-sphere.

History on four-dimensional groups

• 1889 Édouard Goursat, Sur les substitutions orthogonales et les divisions régulières de l'espace, Annales scientifiques de l'École Normale Supérieure, Sér. 3, 6, (pp. 9–102, pp. 80–81 tetrahedra), Goursat tetrahedron
• 1951, A. C. Hurley, Finite rotation groups and crystal classes in four dimensions, Proceedings of the Cambridge Philosophical Society, vol. 47, issue 04, p. 650^[1]
• 1962 A. L. MacKay Bravais Lattices in Four-dimensional Space^[2]
• 1964 Patrick du Val, Homographies, quaternions and rotations, quaternion-based 4D point groups
• 1975 Jan Mozrzymas, Andrzej Solecki, R4 point groups, Reports on Mathematical Physics, Volume 7, Issue 3, p. 363-394 ^[3]
• 1978 H. Brown, R. Bülow, J. Neubüser, H. Wondratschek and H. Zassenhaus, Crystallographic Groups of Four-Dimensional Space.^[4]
• 1982 N. P. Warner, The symmetry groups of the regular tessellations of S2 and S3 ^[5]
• 1985 E. J. W. Whittaker, An atlas of hyperstereograms of the four-dimensional crystal classes
• 1985 H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, Coxeter notation for 4D point groups
• 2003 John Conway and Smith, On Quaternions and Octonions, Completed quaternion-based 4D point groups
• 2015 N. W. Johnson Geometries and Transformations, Extended Coxeter notation for 4D point groups

Isometries of 4D point symmetry

There are four basic isometries of 4-dimensional point symmetry: reflection symmetry, rotational symmetry, rotoreflection, and double rotation.

Enumeration of groups

For cross-referencing, also given here are quaternion based notations by Patrick du Val (1964)^[6] and John Conway (2003).^[7] Conway's notation allows the order of the group to be computed as a product of elements with chiral polyhedral group orders: (T=12, O=24, I=60). In Conway's notation, a (±) prefix implies central inversion, and a suffix (.2) implies mirror symmetry. Similarly Du Val's notation has an asterisk (*) superscript for mirror symmetry.

Involution groups

There are five involutional groups: no symmetry [ ]⁺, reflection symmetry [ ], 2-fold rotational symmetry [2]⁺, 2-fold rotoreflection [2⁺,2⁺], and central point symmetry [2⁺,2⁺,2⁺] as a 2-fold double rotation.

Rank 4 Coxeter groups

The 16-cell, with construction , projected onto a 3-sphere show the symmetry of [2,2,2]. The curved edges can be seen as six great circles, each circle represents the intersection pairs of mirrors on the 3-sphere.

A polychoric group is one of five symmetry groups of the 4-dimensional regular polytopes. There are also three polyhedral prismatic groups, and an infinite set of duoprismatic groups. Each group defined by a Goursat tetrahedron fundamental domain bounded by mirror planes. The dihedral angles between the mirrors determine order of dihedral symmetry. The Coxeter–Dynkin diagram is a graph where nodes represent mirror planes, and edges are called branches, and labeled by their dihedral angle order between the mirrors.

The term polychoron (plural polychora, adjective polychoric), from the Greek roots poly ("many") and choros ("room" or "space") and is advocated^[8] by Norman Johnson and George Olshevsky in the context of uniform polychora (4-polytopes), and their related 4-dimensional symmetry groups.^[9]

Rank 4 Coxeter groups allow a set of 4 mirrors to span 4-space, and divides the 3-sphere into tetrahedral fundamental domains. Lower rank Coxeter groups can only bound hosohedron or hosotope fundamental domains on the 3-sphere.

Like the 3D polyhedral groups, the names of the 4D polychoric groups given are constructed by the Greek prefixes of the cell counts of the corresponding triangle-faced regular polytopes.^[10] Extended symmetries exist in uniform polychora with symmetric ring-patterns within the Coxeter diagram construct. Chiral symmetries exist in alternated uniform polychora. The groups are named in this article in Coxeter's Bracket notation (1985).^[11] Coxeter notation has a direct correspondence the Coxeter diagram like [3,3,3], [4,3,3], [3^1,1,1], [3,4,3], [5,3,3], and [p,2,q]. These groups bound the 3-sphere into identical hyperspherical tetrahedral domains. The number of domains is the order of the group. The number of mirrors for an irreducible group is nh/2, where h is the Coxeter group's Coxeter number, n is the dimension (4).^[12]

Only irreducible groups have Coxeter numbers, but duoprismatic groups [p,2,p] can be doubled to [[p,2,p]] by adding a 2-fold gyration to the fundamental domain, and this gives an effective Coxeter number of 2p, for example the [4,2,4] and its full symmetry B₄, [4,3,3] group with Coxeter number 8.

Weyl group	Conway Quaternion	Abstract structure	Coxeter diagram		Coxeter notation	Order	Commutator subgroup	Coxeter number (h)	Mirrors (m)
Full polychoric groups
A4	+1/60[I×I].21	S5			[3,3,3]	120	[3,3,3]+	5		10
D4	±1/3[T×T].2	1/2.2S4			[31,1,1]	192	[31,1,1]+	6		12
B4	±1/6[O×O].2	2S4 = S2≀S4			[4,3,3]	384		8	4	12
F4	±1/2[O×O].23	3.2S4			[3,4,3]	1152	[3+,4,3+]	12	12	12
H4	±[I×I].2	2.(A5×A5).2			[5,3,3]	14400	[5,3,3]+	30		60
Full polyhedral prismatic groups
A3A1	+1/24[O×O].23	S4×D1			[3,3,2] = [3,3]×[ ]	48	[3,3]+	-		6	1
B3A1	±1/24[O×O].2	S4×D1			[4,3,2] = [4,3]×[ ]	96		-	3	6	1
H3A1	±1/60[I×I].2	A5×D1			[5,3,2] = [5,3]×[ ]	240	[5,3]+	-		15	1
Full duoprismatic groups
4A1 = 2D2	±1/2[D4×D4]	D14 = D22			[2,2,2] = [ ]4 = [2]2	16	[ ]+	4	1	1	1	1
D2B2	±1/2[D4×D8]	D2×D4			[2,2,4] = [2]×[4]	32	[2]+	-	1	1	2	2
D2A2	±1/2[D4×D6]	D2×D3			[2,2,3] = [2]×[3]	24	[3]+	-	1	1	3
D2G2	±1/2[D4×D12]	D2×D6			[2,2,6] = [2]×[6]	48		-	1	1	3	3
D2H2	±1/2[D4×D10]	D2×D5			[2,2,5] = [2]×[5]	40	[5]+	-	1	1	5
2B2	±1/2[D8×D8]	D42			[4,2,4] = [4]2	64	[2+,2,2+]	8	2	2	2	2
B2A2	±1/2[D8×D6]	D4×D3			[4,2,3] = [4]×[3]	48	[2+,2,3+]	-	2	2	3
B2G2	±1/2[D8×D12]	D4×D6			[4,2,6] = [4]×[6]	96		-	2	2	3	3
B2H2	±1/2[D8×D10]	D4×D5			[4,2,5] = [4]×[5]	80	[2+,2,5+]	-	2	2	5
2A2	±1/2[D6×D6]	D32			[3,2,3] = [3]2	36	[3+,2,3+]	6	3		3
A2G2	±1/2[D6×D12]	D3×D6			[3,2,6] = [3]×[6]	72		-	3		3	3
2G2	±1/2[D12×D12]	D62			[6,2,6] = [6]2	144		12	3	3	3	3
A2H2	±1/2[D6×D10]	D3×D5			[3,2,5] = [3]×[5]	60	[3+,2,5+]	-	3		5
G2H2	±1/2[D12×D10]	D6×D5			[6,2,5] = [6]×[5]	120		-	3	3	5
2H2	±1/2[D10×D10]	D52			[5,2,5] = [5]2	100	[5+,2,5+]	10	5		5
In general, p,q=2,3,4...
2I2(2p)	±1/2[D4p×D4p]	D2p2			[2p,2,2p] = [2p]2	16p2	[p+,2,p+]	2p	p	p	p	p
2I2(p)	±1/2[D2p×D2p]	Dp2			[p,2,p] = [p]2	4p2		2p	p		p
I2(p)I2(q)	±1/2[D4p×D4q]	D2p×D2q			[2p,2,2q] = [2p]×[2q]	16pq	[p+,2,q+]	-	p	p	q	q
I2(p)I2(q)	±1/2[D2p×D2q]	Dp×Dq			[p,2,q] = [p]×[q]	4pq		-	p		q

The symmetry order is equal to the number of cells of the regular polychoron times the symmetry of its cells. The omnitruncated dual polychora have cells that match the fundamental domains of the symmetry group.

Nets for convex regular 4-polytopes and omnitruncated duals

Symmetry	A4	D4	B4	F4	H4
4-polytope	5-cell	demitesseract	tesseract	24-cell	120-cell
Cells	5 {3,3}	16 {3,3}	8 {4,3}	24 {3,4}	120 {5,3}
Cell symmetry	[3,3], order 24		[4,3], order 48		[5,3], order 120
Coxeter diagram		=
4-polytope net
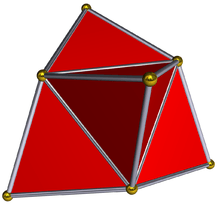Omnitruncation	omni. 5-cell	omni. demitesseract	omni. tesseract	omni. 24-cell	omni. 120-cell
Omnitruncation dual net
Coxeter diagram
Cells	5×24 = 120	(16/2)×24 = 192	8×48 = 384	24×48 = 1152	120×120 = 14400

Chiral subgroups

Direct subgroups of the reflective 4-dimensional point groups are:

Coxeter notation		Conway Quaterion	Structure	Order	Gyration axes
Polychoric groups
	[3,3,3]+	+1/60[I×I]	A5	60			103	102
	[[3,3,3]]+	±1/60[I×I]	A5×C2	120			103	(10+?)2
	[31,1,1]+	±1/3[T×T]	1/2.2A4	96			163	?2
	[4,3,3]+	±1/6[O×O]	2A4 = A2≀A4	192		64	163	?2
	[3,4,3]+	±1/2[O×O]	3.2A4	576	184	163	163	722
	[3+,4,3+]	±[T×T]		288		163	163	(72+18)2
	[[3+,4,3+]]	±[O×T]		576			323	(72+18+?)2
	[[3,4,3]]+	±[O×O]		1152	184		323	(72+?)2
	[5,3,3]+	±[I×I]	2.(A5×A5)	7200		725	2003	4502
Polyhedral prismatic groups
	[3,3,2]+	+1/24[O×O]	A4×C2	24		43	43	(6+6)2
	[4,3,2]+	±1/24[O×O]	S4×C2	96		64	83	(3+6+12)2
	[5,3,2]+	±1/60[I×I]	A5×C2	240		125	203	(15+30)2
Duoprismatic groups
	[2,2,2]+	+1/2[D4×D4]		8		12	12	42
	[3,2,3]+	+1/2[D6×D6]		18		13	13	92
	[4,2,4]+	+1/2[D8×D8]		32		14	14	162
(p,q=2,3,4...)
	[p,2,p]+	+1/2[D2p×D2p]		2p2		1p	1p	(pp)2
	[p,2,q]+	+1/2[D2p×D2q]		2pq		1p	1q	(pq)2
	[p+,2,q+]	+[Cp×Cq]	Cp×Cq	pq		1p	1q

Pentachoric symmetry

• Pentachoric group – A₄, [3,3,3], (), order 120, (Du Val #51' (I^†/C₁;I/C₁)^†*, Conway +¹/₆₀[I×I].2₁), named for the 5-cell (pentachoron), given by ringed Coxeter diagram . It is also sometimes called the hyper-tetrahedral group for extending the tetrahedral group [3,3]. There are 10 mirror hyperplanes in this group. It is isomorphic to the abstract symmetric group, S₅.
  • The extended pentachoric group, Aut(A₄), 3,3,3, (The doubling can be hinted by a folded diagram, ), order 240, (Du Val #51 (I^†*/C₂;I/C₂)^†*, Conway ±¹/₆₀[I×I].2). It is isomorphic to the direct product of abstract groups: S₅×C₂.
    • The chiral extended pentachoric group is 3,3,3⁺, (), order 120, (Du Val #32 (I^†/C₂;I/C₂)^†, Conway ±¹/₆₀[IxI]). This group represents the construction of the omnisnub 5-cell, , although it can not be made uniform. It is isomorphic to the direct product of abstract groups: A₅×C₂.
  • The chiral pentachoric group is [3,3,3]⁺, (), order 60, (Du Val #32' (I^†/C₁;I/C₁)^†, Conway +¹/₆₀[I×I]). It is isomorphic to the abstract alternating group, A₅.
    • The extended chiral pentachoric group is [[3,3,3]⁺], order 120, (Du Val #51" (I^†/C₁;I/C₁)_–^†*, Conway +¹/₆₀[IxI].2₃). Coxeter relates this group to the abstract group (4,6|2,3).^[13] It is also isomorphic to the abstract symmetric group, S₅.

Hexadecachoric symmetry

• Hexadecachoric group – B₄, [4,3,3], (), order 384, (Du Val #47 (O/V;O/V)^*, Conway ±¹/₆[O×O].2), named for the 16-cell (hexadecachoron), . There are 16 mirror hyperplanes in this group, which can be identified in 2 orthogonal sets: 12 from a [3^1,1,1] subgroup, and 4 from a [2,2,2] subgroup. It is also called a hyper-octahedral group for extending the 3D octahedral group [4,3], and the tesseractic group for the tesseract, .
  • The chiral hexadecachoric group is [4,3,3]⁺, (), order 192, (Du Val #27 (O/V;O/V), Conway ±¹/₆[O×O]). This group represents the construction of an omnisnub tesseract, , although it can not be made uniform.
  • The ionic diminished hexadecachoric group is [4,(3,3)⁺], (), order 192, (Du Val #41 (T/V;T/V)^*, Conway ±¹/₃[T×T].2). This group leads to the omnisnub 24-cell with construction .
  • The half hexadecachoric group is [1⁺,4,3,3], ( = ), order 192, and same as the #demitesseractic symmetry: [3^1,1,1]. This group is expressed in the tesseract alternated construction of the 16-cell, = .
    • The group [1⁺,4,(3,3)⁺], ( = ), order 96, and same as the chiral demitesseractic group [3^1,1,1]⁺ and also is the commutator subgroup of [4,3,3].
  • A high-index reflective subgroup is the prismatic octahedral symmetry, [4,3,2] (), order 96, subgroup index 4, (Du Val #44 (O/C₂;O/C₂)^*, Conway ±¹/₂₄[O×O].2). The truncated cubic prism has this symmetry with Coxeter diagram and the cubic prism is a lower symmetry construction of the tesseract, as .
    • Its chiral subgroup is [4,3,2]⁺, (), order 48, (Du Val #26 (O/C₂;O/C₂), Conway ±¹/₂₄[O×O]). An example is the snub cubic antiprism, , although it can not be made uniform.
    • The ionic subgroups are:
      • [(3,4)⁺,2], (), order 48, (Du Val #44b' (O/C₁;O/C₁)₋^*, Conway +¹/₂₄[O×O].2₁). The snub cubic prism has this symmetry with Coxeter diagram .
        • [(3,4)⁺,2⁺], (), order 24, (Du Val #44' (T/C₂;T/C₂)₋^*, Conway +¹/₁₂[T×T].2₁).
      • [4,3⁺,2], (), order 48, (Du Val #39 (T/C₂;T/C₂)_c^*, Conway ±¹/₁₂[T×T].2).
        • [4,3⁺,2,1⁺] = [4,3⁺,1] = [4,3⁺], ( = ), order 24, (Du Val #44" (T/C₂;T/C₂)^*, Conway +¹/₁₂[T×T].2₃). This is the 3D pyritohedral group, [4,3⁺].
        • [3⁺,4,2⁺], (), order 24, (Du Val #21 (T/C₂;T/C₂), Conway ±¹/₁₂[T×T]).
      • [3,4,2⁺], (), order 48, (Du Val #39' (T/C₂;T/C₂)₋^*, Conway ±¹/₁₂[T×T].2).
      • [4,(3,2)⁺], (), order 48, (Du Val #40b' (O/C₁;O/C₁)₋^*, Conway +¹/₂₄[O×O].2₁).
    • A half subgroup [4,3,2,1⁺] = [4,3,1] = [4,3], ( = ), order 48 (Du Val #44b" (O/C₁;O/C₁)_c^*, Conway +¹/₂₄[O×O].2₃). It is called the octahedral pyramidal group and is 3D octahedral symmetry, [4,3]. A cubic pyramid can have this symmetry, with Schläfli symbol: { } ∨ {4,3}.
      

      [4,3], , octahedral pyramidal group is isomorphic to 3d octahedral symmetry
      • A chiral half subgroup [(4,3)⁺,2,1⁺] = [4,3,1]⁺ = [4,3]⁺, ( = ), order 24 (Du Val #26b' (O/C₁;O/C₁), Conway +¹/₂₄[O×O]). This is the 3D chiral octahedral group, [4,3]⁺. A snub cubic pyramid can have this symmetry, with Schläfli symbol: { } ∨ sr{4,3}.
  • Another high-index reflective subgroup is the prismatic tetrahedral symmetry, [3,3,2], (), order 48, subgroup index 8, (Du Val #40b" (O/C₁;O/C₁)^*, Conway +¹/₂₄[O×O].2₃).
    • The chiral subgroup is [3,3,2]⁺, (), order 24, (Du Val #26b" (O/C₁;O/C₁), Conway +¹/₂₄[O×O]). An example is the snub tetrahedral antiprism, , although it can not be made uniform.
    • The ionic subgroup is [(3,3)⁺,2], (), order 24, (Du Val #39b' (T/C₁;T/C₁)_c^*, Conway +¹/₁₂[T×T].2₃). An example is the snub tetrahedral prism, .
    • The half subgroup is [3,3,2,1⁺] = [3,3,1] = [3,3], ( = ), order 24, (Du Val #39b" (T/C₁;T/C₁)₋^*, Conway +¹/₁₂[T×T].2₁). It is called the tetrahedral pyramidal group and is the 3D tetrahedral group, [3,3]. A regular tetrahedral pyramid can have this symmetry, with Schläfli symbol: { } ∨ {3,3}.
      

      [3,3], , tetrahedral pyramidal group is isomorphic to 3d tetrahedral symmetry
      • The chiral half subgroup [(3,3)⁺,2,1⁺] = [3,3]⁺( = ), order 12, (Du Val #21b' (T/C₁;T/C₁), Conway +¹/₁₂[T×T]). This is the 3D chiral tetrahedral group, [3,3]⁺. A snub tetrahedral pyramid can have this symmetry, with Schläfli symbol: { } ∨ sr{3,3}.
  • Another high-index radial reflective subgroup is [4,(3,3)^*], index 24, removes mirrors with order-3 dihedral angles, creating [2,2,2] (), order 16. Others are [4,2,4] (), [4,2,2] (), with subgroup indices 6 and 12, order 64 and 32. These groups are lower symmetries of the tesseract: (), (), and (). These groups are #duoprismatic symmetry.

Icositetrachoric symmetry

• Icositetrachoric group – F₄, [3,4,3], (), order 1152, (Du Val #45 (O/T;O/T)^*, Conway [O×O].2₃), named for the 24-cell (icositetrachoron), . There are 24 mirror planes in this symmetry, which can be decomposed into two orthogonal sets of 12 mirrors in demitesseractic symmetry [3^1,1,1] subgroups, as [3^*,4,3] and [3,4,3^*], as index 6 subgroups.
  • The extended icositetrachoric group, Aut(F₄), 3,4,3, () has order 2304, (Du Val #48 (O/O;O/O)^*, Conway ±[O×O].2).
    • The chiral extended icositetrachoric group, 3,4,3⁺, () has order 1152, (Du Val #25 (O/O;O/O), Conway ±[OxO]). This group represents the construction of the omnisnub 24-cell, , although it can not be made uniform.
  • The ionic diminished icositetrachoric groups, [3⁺,4,3] and [3,4,3⁺], ( or ), have order 576, (Du Val #43 (T/T;T/T)^*, Conway ±[T×T].2). This group leads to the snub 24-cell with construction or .
    • The double diminished icositetrachoric group, [3⁺,4,3⁺] (the double diminishing can be shown by a gap in the diagram 4-branch: ), order 288, (Du Val #20 (T/T;T/T), Conway ±[T×T]) is the commutator subgroup of [3,4,3].
      • It can be extended as [[3⁺,4,3⁺]], () order 576, (Du Val #23 (T/T;O/O), Conway ±[OxT]).
  • The chiral icositetrachoric group is [3,4,3]⁺, (), order 576, (Du Val #28 (O/T;O/T), Conway ±¹/₂[O×O]).
    • The extended chiral icositetrachoric group, [[3,4,3]⁺] has order 1152, (Du Val #46 (O/T;O/T)₋^*, Conway ±¹/₂[OxO].2). Coxeter relates this group to the abstract group (4,8|2,3).^[13]

Demitesseractic symmetry

• Demitesseractic group – D₄, [3^1,1,1], [3^1,1,3] or [1⁺,4,3,3], ( = ), order 192, (Du Val #42 (T/V;T/V)₋^*, Conway ±¹/₃[T×T].2), named for the (demitesseract) 4-demicube construction of the 16-cell, or . There are 12 mirrors in this symmetry group.
  • There are two types of extended symmetries by adding mirrors: <[3,3^1,1]> which becomes [4,3,3] by bisecting the fundamental domain by a mirror, with 3 orientations possible; and the full extended group [3[3^1,1,1]] becomes [3,4,3].
  • The chiral demitesseractic group is [3^1,1,1]⁺ or [1⁺,4,(3,3)⁺], ( = ), order 96, (Du Val #22 (T/V;T/V), Conway ±¹/₃[T×T]). This group leads to the snub 24-cell with construction = .

Hexacosichoric symmetry

• Hexacosichoric group – H₄, [5,3,3], (), order 14400, (Du Val #50 (I/I;I/I)^*, Conway ±[I×I].2), named for the 600-cell (hexacosichoron), . It is also sometimes called the hyper-icosahedral group for extending the 3D icosahedral group [5,3], and hecatonicosachoric group or dodecacontachoric group from the 120-cell, .
  • The chiral hexacosichoric group is [5,3,3]⁺, (), order 7200, (Du Val #30 (I/I;I/I), Conway ±[I×I]). This group represents the construction of the snub 120-cell, , although it can not be made uniform.
  • A high-index reflective subgroup is the prismatic icosahedral symmetry, [5,3,2], (), order 240, subgroup index 60, (Du Val #49 (I/C₂;I/C₂)^*, Conway ±¹/₆₀[IxI].2).
    • Its chiral subgroup is [5,3,2]⁺, (), order 120, (Du Val #31 (I/C₂;I/C₂), Conway ±¹/₆₀[IxI]). This group represents the construction of the snub dodecahedral antiprism, , although it can't be made uniform.
    • An ionic subgroup is [(5,3)⁺,2], (), order 120, (Du Val #49' (I/C₁;I/C₁)^*, Conway +¹/₆₀[IxI].2₁). This group represents the construction of the snub dodecahedral prism, .
    • A half subgroup is [5,3,2,1⁺] = [5,3,1] = [5,3], ( = ), order 120, (Du Val #49" (I/C₁;I/C₁)₋^*, Conway +¹/₆₀[IxI].2₃). It is called the icosahedral pyramidal group and is the 3D icosahedral group, [5,3]. A regular dodecahedral pyramid can have this symmetry, with Schläfli symbol: { } ∨ {5,3}.
      

      [5,3], , icosahedral pyramidal group is isomorphic to 3d icosahedral symmetry
      • A chiral half subgroup is [(5,3)⁺,2,1⁺] = [5,3,1]⁺ = [5,3]⁺, ( = ), order 60, (Du Val #31' (I/C₁;I/C₁), Conway +¹/₆₀[IxI]). This is the 3D chiral icosahedral group, [5,3]⁺. A snub dodecahedral pyramid can have this symmetry, with Schläfli symbol: { } ∨ sr{5,3}.

Duoprismatic symmetry

• Duoprismatic groups – [p,2,q], (), order 4pq, exist for all 2 ≤ p,q < ∞. There are p+q mirrors in this symmetry, which are trivially decomposed into two orthogonal sets of p and q mirrors of dihedral symmetry: [p] and [q].
  • The chiral subgroup is [p,2,p]⁺,(), order 2pq. It can be doubled as [[2p,2,2p]⁺].
  • If p and q are equal, [p,2,p], (), the symmetry can be doubled as p,2,p, ().
    • Doublings: [[p⁺,2,p⁺]], (), [[2p,2⁺,2p]], [[2p⁺,2⁺,2p⁺]].
  • [p,2,∞], (), it represents a line groups in 3-space,
  • [∞,2,∞], () it represents the Euclidean plane symmetry with two sets of parallel mirrors and a rectangular domain (orbifold *2222).
  • Subgroups include: [p⁺,2,q], (), [p,2,q⁺], (), [p⁺,2,q⁺], ().
  • And for even values: [2p,2⁺,2q], (), [2p,2⁺,2q⁺], (), [(p,2)⁺,2q], (), [2p,(2,q)⁺], (), [(p,2)⁺,2q⁺], (), [2p⁺,(2,q)⁺], (), [2p⁺,2⁺,2q⁺], ().
• Digonal duoprismatic group – [2,2,2], (), order 16.
  • The chiral subgroup is [2,2,2]⁺, (), order 8.
  • Extended 2,2,2, (), order 32. The 4-4 duoprism has this extended symmetry, .
    • The chiral extended group is 2,2,2⁺, order 16.
    • Extended chiral subgroup is [[2,2,2]⁺], order 16, with rotoreflection generators. It is isomorphic to the abstract group (4,4|2,2).
  • Other extended [(3,3)[2,2,2]]=[4,3,3], order 384, #Hexadecachoric symmetry. The tesseract has this symmetry, as or .
  • Ionic diminished subgroups is [2⁺,2,2], order 8.
    • The double diminished subgroup is [2⁺,2,2⁺], order 4.
      • Extended as [[2⁺,2,2⁺]], order 8.
    • The rotoreflection subgroups are [2⁺,2⁺,2], [2,2⁺,2⁺], [2⁺,(2,2)⁺], [(2,2)⁺,2⁺] order 4.
    • The triple diminished subgroup is [2⁺,2⁺,2⁺], (), order 2. It is a 2-fold double rotation and a 4D central inversion.
  • Half subgroup is [1⁺,2,2,2]=[1,2,2], order 8.
• Triangular duoprismatic group – [3,2,3], , order 36.
  • The chiral subgroup is [3,2,3]⁺, order 18.
  • Extended 3,2,3, order 72. The 3-3 duoprism has this extended symmetry, .
    • The chiral extended group is 3,2,3⁺, order 36.
    • Extended chiral subgroup is [[3,2,3]⁺], order 36, with rotoreflection generators. It is isomorphic to the abstract group (4,4|2,3).
  • Other extended [[3],2,3], [3,2,[3]], order 72, and are isomorphic to [6,2,3] and [3,2,6].
  • And [[3],2,[3]], order 144, and is isomorphic to [6,2,6].
  • And [[[3],2,[3]]], order 288, isomorphic to 6,2,6. The 6–6 duoprism has this symmetry, as or .
  • Ionic diminished subgroups are [3⁺,2,3], [3,2,3⁺], order 18.
    • The double diminished subgroup is [3⁺,2,3⁺], order 9.
      • Extended as [[3⁺,2,3⁺]], order 18.
  • A high index subgroup is [3,2] , order 12, index 3, which is isomorphic to the dihedral symmetry in three dimensions group, [3,2], D_3h.
    • [3,2]⁺, order 6
• Square duoprismatic group – [4,2,4], , order 64.
  • The chiral subgroup is [4,2,4]⁺, order 32.
  • Extended 4,2,4, order 128. The 4–4 duoprism has this extended symmetry, .
    • The chiral extended group is 4,2,4⁺, order 64.
    • Extended chiral subgroup is [[4,2,4]⁺], order 64, with rotoreflection generators. It is isomorphic to the abstract group (4,4|2,4).
  • Other extended [[4],2,4], [4,2,[4]], order 128, and are isomorphic to [8,2,4] and [4,2,8]. The 4–8 duoprism has this symmetry, as or .
  • And [[4],2,[4]], order 256, and is isomorphic to [8,2,8].
  • And [[[4],2,[4]]], order 288, isomorphic to 8,2,8. The 8–8 duoprism has this symmetry, as or .
  • Ionic diminished subgroups are [4⁺,2,4], [4,2,4⁺], order 32.
    • The double diminished subgroup is [4⁺,2,4⁺], order 16.
      • Extended as [[4⁺,2,4⁺]], order 32.
    • The rotoreflection subgroups are [4⁺,2⁺,4], [4,2⁺,4⁺], [4⁺,(2,4)⁺], [(4,2)⁺,4⁺] order 16.
    • The triple diminished subgroup is [4⁺,2⁺,4⁺], order 8.
  • Half subgroups are [1⁺,4,2,4]=[2,2,4], [4,2,4,1⁺]=[4,2,2], order 16.
    • [1⁺,4,2,4]⁺=[2,2,4]⁺, [4,2,4,1⁺]⁺=[4,2,2]⁺, order 8.
  • Half again subgroup is [1⁺,4,2,4,1⁺]=[2,2,2], order 8.
    • [1⁺,4,2,4,1⁺]⁺ = [1⁺,4,2⁺,4,1⁺] = [2,2,2]⁺, order 4

Summary

This is a summary of 4-dimensional point groups in Coxeter notation. 227 of them are crystallographic point groups (for particular values of p and q).^[14] (nc) is given for non-crystallographic groups. Some crystallographic group have their orders indexed by their abstract group structure.^[15]

Finite groups
[ ]: Symbol Order [1]+ 1.1 [1] = [ ] 2.1 [2]: Symbol Order [1+,2]+ 1.1 [2]+ 2.1 [2] 4.1 [2,2]: Symbol Order [2+,2+]+ = [(2+,2+,2+)] 1.1 [2+,2+] 2.1 [2,2]+ 4.1 [2+,2] 4.1 [2,2] 8.1 [2,2,2]: Symbol Order [(2+,2+,2+,2+)] = [2+,2+,2+]+ 1.1 [2+,2+,2+] 2.1 [2+,2,2+] 4.1 [(2,2)+,2+] 4 [[2+,2+,2+]] 4 [2,2,2]+ 8 [2+,2,2] 8.1 [(2,2)+,2] 8 [[2+,2,2+]] 8.1 [2,2,2] 16.1 [[2,2,2]]+ 16 [[2,2+,2]] 16 [[2,2,2]] 32	[p]: Symbol Order [p]+ p [p] 2p [p,2]: Symbol Order [p,2]+ 2p [p,2] 4p [2p,2+]: Symbol Order [2p,2+] 4p [2p+,2+] 2p [p,2,2]: Symbol Order [p+,2,2+] 2p [(p,2)+,2+] 2p [p,2,2]+ 4p [p,2,2+] 4p [p+,2,2] 4p [(p,2)+,2] 4p [p,2,2] 8p [2p,2+,2]: Symbol Order [2p+,2+,2+] 2p [2p+,2+,2] 4p [2p+,(2,2)+] 4p [2p,(2,2)+] 8p [2p,2+,2] 8p	[p,2,q]: Symbol Order [p+,2,q+] pq [p,2,q]+ 2pq [p+,2,q] 2pq [p,2,q] 4pq [(p,2)+,2q]: Symbol Order [(p,2)+,2q+] 2pq [(p,2)+,2q] 4pq [2p,2+,2q]: Symbol Order [2p+,2+,2q+] 2pq [((2p,2)+,(2q,2)+)] 4pq [2p,2+,2q+] 4pq [2p,2+,2q] 8pq [2p,2,2q] 16pq [[p,2,p]]: Symbol Order [[p+,2,p+]] 2p2 [[p,2,p]]+ 4p2 [[p,2,p]+] 4p2 [[p,2,p]] 8p2 [[2p,2+,2p]]: Symbol Order [[2p+,2+,2p+]] 4p2 [[((2p,2)+,(2p,2)+)]] 8p2 [[2p,2+,2p]] 16p2 [[2p,2,2p]] 32p2	[3,3,2]: Symbol Order [(3,3)Δ,2,1+] ≅ [2,2]+ 4 [(3,3)Δ,2] ≅ [2,(2,2)+] 8 [(3,3)⅄,2,1+] ≅ [4,2+] 8 [(3,3)+,2,1+] = [3,3]+ 12.5 [(3,3)⅄,2] ≅ [2,4,2+] 16 [3,3,2,1+] = [3,3] 24 [(3,3)+,2] 24.10 [3,3,2]+ 24.10 [3,3,2] 48.36 [4,3,2]: Symbol Order [1+,4,3+,2,1+] = [3,3]+ 12 [3+,4,2+] 24 [(3,4)+,2+] 24 [1+,4,3+,2] = [(3,3)+,2] 24.10 [3+,4,2,1+] = [3+,4] 24.10 [(4,3)+,2,1+] = [4,3]+ 24.15 [1+,4,3,2,1+] = [3,3] 24 [1+,4,(3,2)+] = [3,3,2]+ 24 [3,4,2+] 48 [4,3+,2] 48.22 [4,(3,2)+] 48 [(4,3)+,2] 48.36 [1+,4,3,2] = [3,3,2] 48.36 [4,3,2,1+] = [4,3] 48.36 [4,3,2]+ 48.36 [4,3,2] 96.5 [5,3,2]: Symbol Order [(5,3)+,2,1+] = [5,3]+ 60.13 [5,3,2,1+] = [5,3] 120.2 [(5,3)+,2] 120.2 [5,3,2]+ 120.2 [5,3,2] 240 (nc)	[31,1,1]: Symbol Order [31,1,1]Δ ≅[[4,2<sup>+</sup>,4]]+ 32 [31,1,1]⅄ 64 [31,1,1]+ 96.1 [31,1,1] 192.2 <[3,31,1]> = [4,3,3] 384.1 [3[31,1,1]] = [3,4,3] 1152.1 [3,3,3]: Symbol Order [3,3,3]+ 60.13 [3,3,3] 120.1 [[3,3,3]]+ 120.2 [[3,3,3]+] 120.1 [[3,3,3]] 240.1 [4,3,3]: Symbol Order [1+,4,(3,3)Δ] = [31,1,1]Δ ≅[[4,2<sup>+</sup>,4]]+ 32 [4,(3,3)Δ] = [2+,4[2,2,2]+] ≅[[4,2<sup>+</sup>,4]] 64 [1+,4,(3,3)⅄] = [31,1,1]⅄ 64 [1+,4,(3,3)+] = [31,1,1]+ 96.1 [4,(3,3)⅄] ≅ [[4,2,4]] 128 [1+,4,3,3] = [31,1,1] 192.2 [4,(3,3)+] 192.1 [4,3,3]+ 192.3 [4,3,3] 384.1 [3,4,3]: Symbol Order [3+,4,3+] 288.1 [3,4,3]+ 576.2 [3+,4,3] 576.1 [[3+,4,3+]] 576 (nc) [3,4,3] 1152.1 [[3,4,3]]+ 1152 (nc) [[3,4,3]+] 1152 (nc) [[3,4,3]] 2304 (nc) [5,3,3]: Symbol Order [5,3,3]+ 7200 (nc) [5,3,3] 14400 (nc)