Herman ring

The Julia set of the cubic rational function e^2πitz²(z−4)/(1−4z) with t=.6151732... chosen so that the rotation number is (√5−1)/2, which has a Herman ring (shaded).

In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component^[1] where the rational function is conformally conjugate to an irrational rotation of the standard annulus.

Formal definition

Namely if ƒ possesses a Herman ring U with period p, then there exists a conformal mapping

\phi :U\rightarrow \{\zeta :0<r<|\zeta |<1\}

and an irrational number $\theta$ , such that

\phi \circ f^{{\circ p}}\circ \phi ^{{-1}}(\zeta )=e^{{2\pi i\theta }}\zeta .

So the dynamics on the Herman ring is simple.

Name

It was introduced by, and later named after, Michael Herman (1979^[2]) who first found and constructed this type of Fatou component.

Function

Polynomials do not have Herman rings.
Rational functions can have Herman rings
Transcendental entire maps do not have them^[3]

Examples

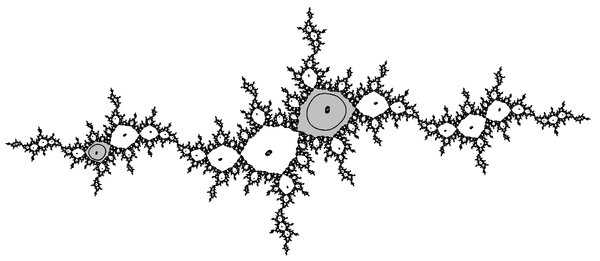
Here is an example of a rational function which possesses a Herman ring.^[1]

f(z)={\frac {e^{{2\pi i\tau }}z^{2}(z-4)}{1-4z}}

where $\tau =0.6151732\dots$ such that the rotation number of ƒ on the unit circle is $({\sqrt {5}}-1)/2$ .

The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.

There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components at the same time.

A rational function

f_{{t,a,b}}(z)=e^{{2\pi it}}z^{3}\,{\frac {1-\overline {a}z}{z-a}}\,{\frac {1-\overline {b}z}{z-b}}

that possesses a Herman ring and some periodic parabolic Fatou components, where

t=0.6141866\dots ,\,a=1/4,\,b=0.0405353-0.0255082i

such that the rotation number of

f_{{t,a,b}}

on the unit circle is

({\sqrt {5}}-1)/2

. The image has been rotated.

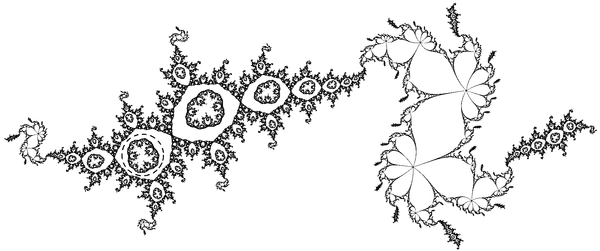
Further, there is a rational function which possesses a Herman ring with period 2.

A rational function possesses Herman rings with period 2

Here the expression of this rational function is

g_{{a,b,c}}(z)={\frac {z^{2}(z-a)}{z-b}}+c,\,

where

{\begin{aligned}a&=0.17021425+0.12612303i,\\b&=0.17115266+0.12592514i,\\c&=1.18521775+0.16885254i.\end{aligned}}

This example was constructed by quasiconformal surgery^[4] from the quadratic polynomial

h(z)=z^{2}-1-{\frac {e^{{{\sqrt {5}}\pi i}}}{4}}

which possesses a Siegel disk with period 2. The parameters a, b, c are calculated by trial and error.

Letting

{\begin{aligned}a&=0.14285933+0.06404502i,\\b&=0.14362386+0.06461542i,{\text{ and}}\\c&=0.18242894+0.81957139i,\end{aligned}}

then the period of one of the Herman ring of g_a,b,c is 3.

Shishikura also given an example:^[5] a rational function which possesses a Herman ring with period 2, but the parameters showed above are different from his.

So there is a question: How to find the formulas of the rational functions which possess Herman rings with higher period?

According to the result of Shishikura, if a rational function ƒ possesses a Herman ring, then the degree of ƒ is at least 3. There also exist meromorphic functions that possess Herman rings.

Herman rings for transcendental meromorphic functions have been studied by T. Nayak. According to a result of Nayak, if there is an omitted value for such a function then Herman rings of period 1 or 2 do not exist. Also, it is proved that if there is only a single pole and at least an omitted value, the function has no Herman ring of any period.

References

1 2 John Milnor, Dynamics in one complex variable: Third Edition, Annals of Mathematics Studies, 160, Princeton Univ. Press, Princeton, NJ, 2006.
↑ Herman, Michael-Robert (1979), "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations", Publications Mathématiques de l'IHÉS (49): 5–233, ISSN 1618-1913, MR 538680
↑ Omitted Values and Herman rings by Tarakanta Nayak.
↑ Mitsuhiro Shishikura, On the quasiconformal surgery of rational functions. Ann. Sci. Ecole Norm. Sup. (4) 20 (1987), no. 1, 1–29.
↑ Mitsuhiro Shishikura, Surgery of complex analytic dynamical systems, in "Dynamical Systems and Nonlinear Oscillations", Ed. by Giko Ikegami, World Scientific Advanced Series in Dynamical Systems, 1, World Scientific, 1986, 93–105.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.