Hamiltonian coloring
Hamiltonian coloring is a type of graph coloring. Hamiltonian coloring uses a concept called detour distance between two vertices of the graph.[1] It has many applications in different areas of science and technology.
Terminologies
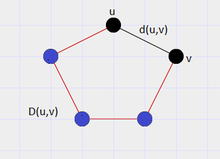
The detour distance between u and v in C5 is 4
Detour distance
The distance between two vertices in a graph is defined as the minimum of lengths of paths connecting those vertices. The detour distance between two vertices, say, u and v is defined as the length of the longest u-v path in the graph.[1] In the case of a tree the detour distance between any two vertices is same as the distance between the two vertices.
References
- 1 2 Chartrand, Gary; Zhang, Ping (2009). "14. Colorings, Distance, and Domination". Chromatic Graph Theory. CRC Press. pp. 397–438.
This article is issued from
Wikipedia.
The text is licensed under Creative Commons - Attribution - Sharealike.
Additional terms may apply for the media files.