Group testing

An illustration of the lightbulb problem with 6 lightbulbs. Here, we connect the first three, and they light up (A). This tells us that the broken bulb must be one of the last three (B). If instead the bulbs did not light up, we could be sure that the broken bulb was among the first three.

In statistics and combinatorial mathematics, group testing refers to any procedure which breaks up the task of locating elements of a set which have certain properties into tests on groups of items, rather than on individual elements. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that is an active area of research today, and has a large amount of utility in a wide range of practical applications.

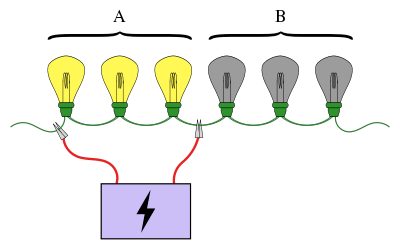
A familiar example of group testing involves a string of lightbulbs connected series, where we know exactly one of the bulbs is broken. The objective is to find the broken bulb using the smallest number of tests (a test is when we connect some of the bulbs to a power supply). A simple approach is to test each bulb individually. However, when there are a large number of bulbs we can be much more efficient if we pool the bulbs into groups. For example, if we connect the first half of the bulbs at once, we can determine which half the broken bulb is in, ruling out half of the bulbs in just one test.

Schemes for carrying out such group testing can be simple or complex and the tests involved at each stage may be different. Schemes in which the tests for the next stage depend on the results of the previous stages are called adaptive procedures, while schemes designed so that all the tests are known beforehand are called non-adaptive procedures. The structure of the scheme of the tests involved in a non-adaptive procedure is known as a pooling design.

Group testing has applications in statistics, biology, computer science medicine and engineering. Modern interest in these testing schemes has been rekindled by the Human Genome Project.^[1]

Basic description and terms

Unlike many areas of Mathematics, the origins of group testing can be traced back to a single report^[2] written by a single person: Robert Dorfman.^[3] The motivation arose during the Second World War when the United States Public Health Service and the Selective service embarked upon a large scale project to weed out all syphilitic men called up for induction. Testing an individual for syphilis involves drawing a blood sample from them and then analysing the sample to determine the presence or absence of syphilis. However, at the time, performing this test was expensive, and testing every soldier individually would have been very cost heavy and inefficient.

Supposing there are $n$ soldiers, this method of testing leads to $n$ separate tests. If a large proportion of the people are infected then this method would be reasonable. However, in the more likely case that only a very small proportion of the men are infected, a much more efficient testing scheme can be achieved. The feasibility of a more effective testing scheme hinges on the following property: we can pool the soldiers into groups, and in each group we can combine blood samples together. We can then test the combined sample to check if at least one soldier in the group has syphilis. This is the central idea behind group testing. If one or more of the soldiers in this group has syphilis, then a test is wasted (more tests need to be performed to find which soldier(s) it was). On the other hand, if no one in the pool has syphilis then many tests are saved, since we can eliminate every soldier in that group with just one test.

The items that cause a group to test positive are generally called defective items (these are the broken lightbulbs, syphilitic men, etc.). We also denote the total number of items as $n$ and write $d$ for the number of defectives if it is assumed to be known.

Classification of group-testing problems

There are two independent classifications group-testing problems; every group-testing problem is either adaptive or non-adaptive, and either probabilistic or combinatorial.

In probabilistic models, the defective items are assumed to follow some probability distribution and the aim is to minimise the expected number of tests needed to identify the defectiveness of every item. On the other hand, with combinatorial group testing, the goal is to minimise the number of tested needed in a 'worst case scenario' – that is, create a minmax algorithm – and no knowledge of the distribution of defectives is assumed.

The other classification, adaptivity, concerns what information we are allowed to use when choosing which items to group into a test. In general, the choice of which items to test can depend on the results of previous tests, as in the above lightbulb problem. An algorithm that proceeds by performing a test, and then using the result (and all past results) to decide which next test to perform, is called adaptive. Conversely, in non-adaptive algorithms, all tests are decided in advance. This idea can be generalised to multistage algorithms, where tests are divided into stages, and every test in the next stage must be decided in advance, with only the knowledge of the results of tests in previous stages. Although adaptive algorithms offer much more freedom in design, it is known that adaptive group-testing algorithms do not improve upon non-adaptive ones by more than a constant factor in the number of tests required to identify the set of defective items.^[4]^[3] In addition to this, non-adaptive methods are often useful in practice because one knows in advance all the tests one needs to perform, allowing for the effective distribution of the testing process.

Variations and extensions

There are many ways we can extend the problem of group testing. One of the most important is called noisy group testing, and deals with a big assumption of the original problem: that testing is error-free. We say that a group-testing problem is noisy when there is some chance that the result of a group test is erroneous (e.g. comes out positive when the test contained no defectives). The Bernoulli noise model assumes this probability is some constant, $q$ , but in general it can depend on the true number of defectives in the test and the number of items tested. For example, we may model the effect of dilution by saying a positive result is more likely when there are more defectives (or more defectives as a fraction of the number tested), present in the test. A noisy algorithm will always have a non-zero probability of making an error (that is, mislabeling an item).

Group testing can be extended by considering scenarios in which there are more than two possible outcomes of a test. For example, a test may have the outcomes $0,1$ and $2^{+}$ , corresponding to there being no defectives, and single defective, or an unknown number of defectives larger than one. More generally we can consider the outcome-set of a test as ${0,1,...,k^{+}}$ for some $k\in \mathbb {N}$ .

Another extension is to consider geometric restrictions on which sets can be tested. The above lightbulb problem is an example of this kind of restriction: we can only test bulbs that appear consecutively. We can also consider testing that happens on a circle, or in general, a net, where the tests are available paths on the graph. Another kind of geometric restriction would be on the maximum number of items that can be tested in a group,^{[lower-alpha 1]} or the group sizes might have to be even and so on. In a similar way, we may want to consider the restriction that any given item can only appear in a certain number of tests.

There are endless ways to continue remixing the basic formula of group testing. For an idea of some of the more exotic variants consider the following. The 'good–mediocre–bad' model, where each item is one of 'good', 'mediocre' or 'bad', and the result of a test is the type of the 'worst' item in the group. There is also threshold group testing, where the result of a test is positive if the number of defective items in the group is greater than some threshold value or proportion.^[5] Group testing with inhibitors is a variant with applications in molecular biology. Here, there is a third class of items called inhibitors, and the result of a test is positive if it contains at least one defective and no inhibitors.^[6]

History and development

Invention and initial progress

The concept of group testing was first introduced by Robert Dorfman in 1943 in a short report^[2] published in the Notes section of The Annals of Mathematical Statistics.^[3]^{[lower-alpha 2]} Dorfman's report – as with all the early work on group testing – focused on the probabilistic problem, and aimed to use the novel idea of group testing to reduce the expected number of tests needed to weed out all syphilitic men in a given pool of soldiers. The method was simple: put the soldiers into groups of a given size, and use individual testing (testing items in groups of size one) on the positive groups to find which were infected. Dorfman tabulated the optimum group sizes for this strategy against the prevalence rate of defectiveness in the population.

After 1943, group testing remained largely untouched for a number of years. Then in 1957, Sterrett produced an improvement on Dorfman’s procedure.^[8] In this new process we again perform individual testing on the positive groups, but we stop as soon as a defective is identified. Then, the remaining items in the group are tested together, since it is very likely that none of them are defective.

The first thorough treatment of group testing was given by Sobel and Groll in their formative 1959 paper on the subject.^[9] They described five new procedures – in addition to generalisations for when the prevalence rate is unknown – and for the most optimal one, they provided an explicit formula for the expected number of tests it would use. The paper also made the connection between group testing and information theory for the first time, as well as discussing several generalisations of the group-testing problem and providing some new applications of the theory.

Combinatorial group testing

Group testing was first studied in the combinatorial context by Li in 1962,^[10] with the introduction of Li’s $s$ -stage algorithm.^[3] Li proposed an extension of Dorfman's '2-stage algorithm' to an arbitrary number of stages that required no more than $t={\frac {e}{\log(e)}}d\log(n)$ tests to be guaranteed to find $d$ or fewer defectives among $n$ items. The idea was to remove all the items in negative tests, and divide the remaining items into groups as was done with the initial pool. This was to be done $s-1$ times before performing individual testing.

Combinatorial group testing in general was later studied more fully by Katona in 1973.^[11] Katona introduced the matrix representation of non-adaptive group-testing and produced a procedure for finding the defective in the non-adaptive 1-defective case in no more than $t=\lceil \log _{2}(n)\rceil$ tests, which he also proved to be optimal.

In general, finding optimal algorithms for adaptive combinatorial group testing is difficult, and although the computational complexity of group testing has not been determined, it is suspected to be hard in some complexity class.^[3] However, an important breakthrough occurred in 1972, with the introduction of the generalised binary-splitting algorithm.^[12] The generalised binary-splitting algorithm works by performing a binary search on groups that test positive, and is a simple algorithm that finds a single defective in no more than the information-lower-bound number of tests.

In scenarios where there are two or more defectives, the generalised binary-splitting algorithm still produces near-optimal results, requiring at most $d-1$ tests above the information lower bound where $d$ is the number of defectives.^[12] Considerable improvements to this were made in 2013 by Allemann, getting the required number of tests to less than $0.187d+0.5\log _{2}(d)+5.5$ above the information lower bound when $n/d\geq 38$ and $d\geq 10$ .^[13] This was achieved by changing the binary search in the binary-splitting algorithm to a complex set of sub-algorithms with overlapping test groups. As such, the problem of adaptive combinatorial group testing – with a known number or upper bound on the number of defectives – has essentially been solved, with little room for further improvement.

There is an open question as to when individual testing is minmax. Hu, Hwang and Wang showed in 1981 that individual testing is minmax when $n\leq \lfloor (5d+1)/2\rfloor$ , and that it is not minmax when $n>3d$ .^[14] It is currently conjectured that this bound is sharp: that is, individual testing is minmax if and only if $n\leq 3d$ .^[15]^{[lower-alpha 3]} Some progress was made in 2000 by Ricccio and Colbourn, who showed that for large $n$ , individual testing is minmax when $d\geq n/\log _{3/2}(3)\approx 0.369n$ .^[16]

Non-adaptive testing

Turning now to non-adaptive group testing, significant gains can be made by not requiring that the group-testing procedure be certain to succeed, but rather to have some non-zero probability of mis-labelling an item. In particular, it is known that zero-error algorithms require significantly more tests asymptotically (in the number of defective items) than algorithms that allow asymptotically small probabilities of error.^[4]^{[lower-alpha 4]}

In this vein, Chan et al. introduced COMP in 2011, a fast, explicit algorithm that requires no more than $t=ed(1+\delta )\ln(n)$ tests to find up to $d$ defectives in $n$ items with a probability of error no more than $n^{-\delta }$ .^[17] This is within a constant factor of the $t=O(d\log n)$ lower bound.^[4] They also provided a generalisation of this algorithm to a simple noisy model, and similarly produced an explicit performance bound, which was again only a constant (dependent on the likelihood of a failed test) above the corresponding lower bound.^[4]^[17] In general, the number of tests required in the Bernoulli noise case is a constant factor larger than in the noiseless case.^[17]

An extension of the COMP algorithm that added additional post-processing steps was produced Aldridge, Baldassini and Johnson in 2014.^[18] They showed that performance guarantees of this new algorithm, called DD, strictly exceed those of COMP, and that DD is 'essentially optimal' in scenarios where $d^{2}\geq n$ , by comparing it to a hypothetical algorithm that defines a reasonable optimum. The performance of this hypothetical algorithm suggests that there is, and how much, possible room for improvement there is when $d^{2}<n$ .

Formalization of combinatorial group testing

This section formally defines the notions and terms relating to group testing.

The input vector, $\mathbf {x} =(x_{1},x_{2},\dots ,x_{n})$ , is defined to be a binary vector of length $n$ (that is, ${\mathbf {x}}\in \{0,1\}^{n}$ ), with the j-th item being called defective if and only if $x_{j}=1$ . Further, we will refer to any non-defective items as 'good'.

$\mathbf {x}$ is intended to describe the (unknown) set of defective items. The key property of $\mathbf {x}$ is that it is an implicit input. That is to say, we do not have any direct knowledge of what the entries of $\mathbf {x}$ are, other than that which we can infer via some series of 'tests'. This leads us on to our next definition.

Let $\mathbf {x}$ be an input vector. A set, $S\subseteq \{1,2,\dots ,n\}$ is called a test. When testing is noiseless, we say the result of a test is positive when there exists $j\in S$ such that $x_{j}=1$ , and the result is negative otherwise.

We therefore have that the goal of group testing is to come up with a method for choosing a 'short' series of tests that allow us to determine $\mathbf {x}$ , either exactly or with a high degree of certainty.

A group-testing algorithm is said to make an error if it incorrectly labels an item (that is, labels any defective item as non-defective or vice versa). This is not the same thing as the result of a group test being incorrect. An algorithm is called zero-error if the probability that it makes an error is zero.^{[lower-alpha 5]}
We write $t(d,n)$ for the minimum number of tests required to always solve find $d$ defectives among $n$ items with zero probability of error by any group-testing algorithm. For the same quantity but with the restriction that the algorithm is non-adaptive, we write ${\bar {t}}(d,n)$ .

General bounds

Since we can always resort to individual testing by setting $S_{j}=\{j\}$ for each $1\leq j\leq n$ , we have that ${\bar {t}}(d,n)\leq n$ . Also, since any non-adaptive testing procedure can be written as an adaptive algorithm by simply performing all the tests without regard to their outcome, we have that $t(d,n)\leq {\bar {t}}(d,n)$ . Finally, when $0\neq d\neq n$ , there is at least one item whose defectiveness must be determined (by at least one test), and so $1\leq t(d,n)$ .

In summary (when we assume $0\neq d\neq n$ ), $1\leq t(d,n)\leq {\bar {t}}(d,n)\leq n$ .^{[lower-alpha 6]}

Information lower bound

To describe a lower bound we will use the notion of sample space, denoted ${\mathcal {S}}$ , which is simply the set of possible placements of defectives. For any group testing problem with sample space ${\mathcal {S}}$ and group-testing algorithm, we have that $t\geq \lceil \log _{2}{|{\mathcal {S}}|}\rceil$ , where $t$ is the minimum number of tests required to identify all defectives with a zero probability of error. This is called the information lower bound. This bound is derived from the fact that after each test, ${\mathcal {S}}$ is split into two disjoint subsets, each corresponding to one of the two possible outcomes of the test.

However, the information lower bound itself is usually unachievable, even for small problems.^[3] This is because the splitting of ${\mathcal {S}}$ is not arbitrary, since it must be realisable by some test.

In fact, we can generalise the information lower bound to the case where there is a non-zero probability that the algorithm makes an error. In this form, the theorem gives us an upper bound on the probability of success based on the number of tests. For any group-testing algorithm that performs $t$ tests, the probability of success, $\mathbb {P} ({\textrm {success}})$ , satisfies $\mathbb {P} ({\textrm {success}})\leq t/\log _{2}{n \choose d}$ . This can be strengthened to: $\mathbb {P} ({\textrm {success}})\leq {\frac {2^{t}}{n \choose d}}$ .^[17]^[19]

Representation of non-adaptive algorithms

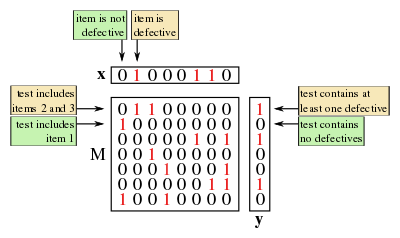
A diagram showing a group testing matrix along with associated vectors, x and y.

A typical group testing setup. A non-adaptive algorithm first chooses the matrix

M

, and is then given the vector y. The problem is then to find an estimate for x.

Algorithms for non-adaptive group testing consist of two distinct phases. First, it is decided how many tests to perform and which items to include in each test. In the second phase, often called the decoding step, the results of each group test are analysed to determine which items are likely to be defective. The first phase is usually encoded in a matrix as follows.

Suppose a non-adaptive group testing procedure for $n$ items consists of the tests $S_{1},S_{2},\dots ,S_{t}$ for some $t\in \mathbb {N} _{\geq 0}$ . The testing matrix for this scheme is the $t\times n$ binary matrix, $M$ , where $(M)_{ij}=1$ if and only if $j\in S_{i}$ (and is zero otherwise).

Thus each column of $M$ represents an item and each row represents a test, with a $1$ in the $(i,j){\textrm {-th}}$ entry indicating that the $i{\textrm {-th}}$ test included the $j{\textrm {-th}}$ item and a $0$ indicating otherwise.

As well as the vector $\mathbf {x}$ (of length $n$ ) that describes the unknown defective set, we now introduce the result vector, which describes the results of each test.

Let $t$ be the number of tests performed by a non-adaptive algorithm. The result vector, $\mathbf {y} =(y_{1},y_{2},\dots ,y_{t})$ , is a binary vector of length $t$ (that is, $\mathbf {y} \in \{0,1\}^{t}$ ) such that $y_{i}=1$ if and only if the result of the $i{\textrm {-th}}$ test was positive (i.e. contained at least one defective.^{[lower-alpha 7]}

We are now in a position to reframe the non-adaptive problem as follows: first we choose some testing matrix, $M$ , after which we are given $\mathbf {y}$ . Then the problem is to analyse $\mathbf {y}$ to find some estimate for $\mathbf {x}$ .

In the simplest noisy case, where there is a constant probability, $q$ , that a group test will have an erroneous result, we consider a random binary vector, $\mathbf {v}$ , where each entry has a probability $q$ of being $1$ , and is $0$ otherwise. We then set ${\hat {\mathbf {y} }}=\mathbf {y} +\mathbf {v}$ , with the usual addition on $(\mathbb {Z} /2\mathbb {Z} )^{n}$ (equivalently this is the element-wise XOR operation). A noisy algorithm must estimate $\mathbf {x}$ using ${\hat {\mathbf {y} }}$ (that is, without direct knowledge of $\mathbf {y}$ ).

Bounds for non-adaptive algorithms

The matrix representation allows us to prove some bounds on non-adaptive group testing. The approach mirrors that of many deterministic designs, where we consider $d$ -separable matrices, as defined below. However, it should be noted the following results are for zero-error procedures. Designs that instead allow asymptotically small probabilities of error can do much better, as discussed at the end of this section.

We say that a binary matrix, $M$ , is $d$ -separable if every Boolean sum (logical OR) of any $d$ of its columns is distinct. Additionally, we write that $M$ is ${\bar {d}}$ -separable if every sum of any of up to $d$ of its columns is distinct. (Note that this is not the same as $M$ being $k$ -separable for every $k\leq d$ .)

When $M$ is a testing matrix, the property of being $d$ -separable ( ${\bar {d}}$ -separable) is equivalent to being able to distinguish between (up to) $d$ defectives. However, it does not guarantee that this will be straightforward. A stronger property, called $d$ -disjunctness does.

A binary matrix, $M$ is called $d$ -disjunct if the Boolean sum of any $d$ columns does not contain any other column.

A useful property of $d$ -disjunct testing matrices is that, with up to $d$ defectives, every non-defective item will appear in at least one test whose outcome is negative. This means we have a simple procedure for finding the defectives: just remove every item that appears in a negative test.

Using these tools the following can be shown for the problem of identifying $d$ defectives among $n$ total items.^[4]

The number of tests needed for an asymptotically small average probability of error scales as $O(d\log n)$ .
The number of tests needed for an asymptotically small maximum probability of error scales as $O(d^{2}\log n)$ .
The number of tests needed for a zero probability of error scales as $O\left({\frac {d^{2}\log n}{\log d}}\right)$ .

Generalized binary-splitting algorithm

An illustration of the generalised binary-splitting algorithm where there are 8 defectives and 135 total items. Here,

2^{\alpha _{1}}=16

, and the first test gives a negative result so every item is declared non-defective. Hence there are

119

remaining items, so

2^{\alpha _{2}}=14

. This second group gives a positive result, so we proceed by binary search to find a defective. Once that is done, we repeat this process, calculating a new

\alpha

using only those items whose defectiveness has not been determined.

The generalized binary-splitting algorithm is an essentially-optimal adaptive group-testing algorithm that proceeds as follows:^[3]^[12]

If $n\leq 2d-2$ , test the $n$ items individually. Otherwise, set $l=n-d+1$ and $\alpha =\lfloor \log {l/d}\rfloor$ .
Test a group of size $2^{\alpha }$ . If the outcome is negative, every item in the group is declared to be non-defective; set $n:=n-2^{\alpha }$ and go to step 1. Otherwise, use a binary search to identify one defective and an unspecified number, called $x$ , of non-defective items; set $n:=n-1-x$ and $d:=d-1$ . Go to step 1.

The generalized binary-splitting algorithm requires no more than $T$ tests where $T={\begin{cases}n&n\leq 2d-2\\(\alpha +2)d+p-1&n\geq 2d-1\end{cases}}$ .^[3]

For $n/d$ large, it can be shown that $T\rightarrow d\log(n/d)$ ,^[3] which compares favorably to the $t={\frac {e}{\log e}}d\log \left({\frac {n}{d}}\right)$ tests required for Li's $s$ -stage algorithm. In fact, the generalized binary-splitting algorithm is close to optimal in the following sense. When $d\geq 2$ we have $T-B_{I}(d,n)\leq (d-1)$ , where $B_{I}(d,n)=\lceil \log _{2}\sum _{i=0}^{d}{n \choose i}\rceil$ is the information lower bound.^[3]^[12]

Non-adaptive algorithms

Non-adaptive group-testing algorithms tend to assume that the number of defectives, or at least a good upper bound on them, is known.^[17] We will denote this quantity $d$ . If no bounds are known, there are non-adaptive algorithms with low query complexity that can help estimate $d$ .^[20]

Combinatorial Orthogonal Matching Pursuit (COMP)

An illustration of the COMP algorithm. COMP identifies item a as being defective and item b as being non-defective. However, it incorrectly labels c as a defective, since it is “hidden” by defective items in every test in which it appears.

Combinatorial Orthogonal Matching Pursuit, or COMP, is a simple non-adaptive group-testing algorithm that forms the basis for the more complicated algorithms that follow in this section.

First, each entry of the testing matrix is chosen i.i.d. to be $1$ with probability $1/d$ and $0$ otherwise.

The decoding step proceeds column-wise (i.e. by item). If every test in which an item appears is positive, then the item is declared defective; otherwise the item is assumed to be non-defective. Or equivalently, if an item appears in any test whose outcome is negative, the item is declared non-defective; otherwise the item is assumed to be defective. Of particular note here is that this algorithm never creates false negatives, though a false positive occurs when all locations with ones in the j-th column of $M$ (corresponding to a non-defective item j) are “hidden” by the ones of other columns corresponding to defective items.

The COMP algorithm requires no more than $ed(1+\delta )\ln(n)$ tests to have an error probability less than or equal to $n^{-\delta }$ .^[17]

In the noisy case, we relax the requirement in the original COMP algorithm that the set of locations of ones in any column of $M$ corresponding to a positive item be entirely contained in the set of locations of ones in the result vector. Instead, we allow for a certain number of “mismatches” – this number of mismatches depends on both the number of ones in each column, and also the noise parameter, $q$ . This noisy COMP algorithm requires no more than $4.36({\sqrt {\delta }}+{\sqrt {1+\delta }})^{2}(1-2q)^{-2}d\log {n}$ tests to achieve an error probability at most $n^{-\delta }$ .^[17]

Definite Defectives (DD)

The definite defectives method (DD) is an extension of the COMP algorithm that attempts to remove any false positives. Performance guarantees for DD have been shown to strictly exceed those of COMP.^[18]

The decoding step uses a useful property of the COMP algorithm: that every item that COMP declares non-defective is certainly non-defective (that is, there are no false negatives). It proceeds as follows:

We first run the COMP algorithm, and remove any non-defectives that it detects. All remaining items are now “possibly defective”
Next the algorithm looks at all the positive tests. If an item appears as the only “possible defective” in a test, then it must be defective, so the algorithm declares it to be defective.
All other items are assumed to be non-defective. The justification for this last step comes from the assumption that the number of defectives is much smaller than the total number of items.

Note that steps 1 and 2 never make a mistake, so the algorithm can only make a mistake if it declares a defective item to be non-defective. Thus the DD algorithm can only create false negatives.

Sequential COMP (SCOMP)

SCOMP (Sequential COMP) is an algorithm that makes use of the fact that DD makes no mistakes until the last step, where we assume remaining items to be defective. Let the set of declared defectives be $K$ . We say that a positive test is explained by $K$ if it contains at least one item in $K$ . The key observation with SCOMP is that the set of defectives found by DD may not explain every positive test, and that every unexplained test must contain a hidden defective.

The algorithm proceeds as follows:

First carry out steps 1 and 2 of the DD algorithm to obtain $K$ , an initial estimate for the set of defectives.
If $K$ explains every positive test, terminate the algorithm: $K$ is our final estimate for the set of defectives.
If there are any unexplained tests, find the “possible defective” that appears in the largest number of unexplained tests, and declare it to be defective (that is, add it to the set $K$ ). Go to step 2.

In simulations, SCOMP has been shown to perform close to optimally.^[18]

Example applications

The generality of the theory of group testing and lends it to many diverse applications, including clone screening, locating electrical shorts;^[3] high speed computer networks;^[21] medical examination, quantity searching, statistics;^[14] machine learning, DNA sequencing;^[22] cryptography;^[23]^[24] and data forensics.^[25] This section provides a brief overview of a small selection of these applications.

Multiaccess channels

An illustration of a multiaccess channel showing a successful message and a message collision.

A multiaccess channel is a communication channel that connects many users at once. Every user can listen and transmit on the channel, but if more than one user transmits at the same time, the signals collide, and are reduced to unintelligible noise. Multiaccess channels are important for various real-world applications, notably wireless computer networks and phone networks.^[26]

A prominent problem with multiaccess channels is how can to assign transmission times to the users so that their messages do not collide. A simple method is to give each user their own time slot in which to transmit, requiring $n$ slots. (This is called time division multiplexing, or TDM.) However, this is very inefficient, since we usually assume that only a few users will want to transmit at any given time – otherwise a multiaccess channel is not practical in the first place.

In the context of group testing, this problem is usually tackled by dividing time into 'epochs'.^[3] We say that an user is active if they have a message at the start of an epoch. (If a message is generated during an epoch, the user only becomes active at the start of the next one.) An epoch ends when every active user has successfully transmitted their message. The problem is now to find all the active users in a given epoch, and schedule a time for them to transmit (if they have not already done so successfully). This is then a group testing problem where the query asks a set of users to attempt a transmission if they are active. The outcomes are $\{0,1,2^{+}\}$ , corresponding respectively to the possible results of a query: no active users, exactly one active user (message successful) or more than one active user (message collision).

Machine learning and compressed sensing

Machine learning is a field of computer science that has many software applications such as DNA classification, fraud detection and targeted advertising. One of the main subfields of machine learning is the 'learning by examples' problem, where the task is to approximate some unknown function when given its value at a number of specific points. As outlined in this section, this function learning problem can be tackled with a group-testing approach.

In a simple version of the problem, we have some unknown function, $f:\{0,1\}^{N}\to \{0,1\}$ where $f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}$ , and ${\textbf {a}}\in \{0,1\}^{N}$ (note that we are using logical arithmetic: addition is logical OR and multiplication is logical AND). Here $\textbf{a}$ is ' $d$ sparse', which means that at most $d\ll N$ of its entries are $1$ . The aim is to construct an approximation to $f$ using $t$ point evaluations, where $t$ is as small as possible. (Exactly recovering $f$ corresponds to zero-error algorithms, whereas $f$ is approximated by algorithms that have a non-zero probability of error.)

In this problem, recovering $f$ is equivalent to finding $\textbf{a}$ . Moreover, $f({\textbf {p}})=1$ if and only if there is some index, $n$ , where ${\textbf {a}}_{n}={\textbf {p}}_{n}=1$ . Thus this problem is analogous to a group-testing problem with $d$ defectives and $n$ total items. The entries of $\textbf{a}$ are the items, which are defective if they are $1$ , ${\textbf {p}}$ specifies a test, and a test is positive if and only if $f({\textbf {p}})=1$ .

In reality, we will often be interested in functions that are more complicated, such as $f:\mathbb {C} ^{N}\to \mathbb {C}$ , again where $f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}$ . To solve this problem, we turn to compressed sensing, which closely related to group testing.

In compressed sensing, the goal is to reconstruct a signal, ${\textbf {v}}\in \mathbb {C} ^{N}$ , by taking a number of measurements. These measurements are modelled as taking the dot product of $\textbf{v}$ with a chosen vector.^{[lower-alpha 8]} The aim is to use a small number of measurements, though this is typically not possible unless something is assumed about the signal. Our assumption here (which is common^[29]^[30]) is that only a small number of entries of $\textbf{v}$ are significant, meaning that they have a large magnitude. Since the measurements are dot products of $\textbf{v}$ , we can write $M{\textbf {v}}={\textbf {q}}$ , where $M$ is a $t\times N$ matrix that describes the set of measurements we choose to make and $\mathbf {q}$ is the set of measurement results. From this construction we can see that compressed sensing is a kind of 'continuous' group testing.

The primary difficulty in compressed sensing is identifying which entries are significant.^[29] Once that is done, there are a variety of methods to estimate the actual values of the entries.^[31] We can approach this task of identification with a simple application of group testing. Here a group test produces a complex number: the sum of the entries that are tested. We then say that a test is positive if it produces a complex number with a large magnitude, which, given the assumption that the significant entries are sparse, indicates that at least one significant entry is contained in the test.

There are explicit deterministic constructions for this type of combinatorial search algorithm, requiring $d2^{(\log \log N)^{O(1)}}$ measurements.^[32] However, as with group-testing, these are sub-optimal, and random constructions (such as COMP) can often recover $f$ sub-linearly in $N$ .^[31]

Data forensics

Data forensics is a field dedicated to finding methods for compiling digital evidence of a crime. Such crimes typically involve an adversary modifying the data, documents or databases of a victim, with examples including the altering of tax records, a virus hiding its presence, or an identity thief modifying personal data.

A common tool in data forensics is the one-way cryptographic hash. This is a function that takes the data, and through a difficult-to-reverse procedure, produces a unique number called a hash.^{[lower-alpha 9]} Hashes, which are often much shorter than the data, allow us to check if the data has been changed without having to wastefully store complete copies of the information: the hash for the current data can be compared with a past hash to determine if any changes have occurred. An unfortunate property of this method is that, although we can tell if the data has been modified, we have no way of determining how: that is, we cannot recover which part of the data has changed.

One way to get around this limitation is to store more hashes – now of subsets of the data structure – to narrow down where the attack has occurred. However, to find the exact location of the attack with a naive approach, we would need to store a hash for every datum in the structure, which would defeat the point of the hashes in the first place. (We may as well store a regular copy of the data.) Group testing can be used to dramatically reduce the number of hashes we need to store. A test becomes a comparison between the stored and current hashes, which is positive when there is a mismatch. This indicates that at least one edited datum (which is taken as defectiveness in this model) is contained in the group that generated the current hash.

In fact, the amount of hashes needed is so low that they, along with the testing matrix they refer to, can even be stored within the organizational structure of the data itself. This means that as far as memory is concerned we can perform the test 'for free'. (This is true with the exception of a master-key/password that is used to secretly determine the hashing function.)

Notes

↑ The original problem that Dorfman studied was of this nature (although he did not account for this), since in practice, only a certain number of blood sera could be pooled before the testing procedure became unreliable. This was the main reason that Dorfman’s procedure was not applied at the time.^[3]
↑ However, as is often the case in mathematics, group testing has been subsequently re-invented multiple times since then, often in the context of applications. For example, Hayes independently came up with the idea to query groups of users in the context of multiaccess communication protocols in 1978.^[7]
↑ This is sometimes referred to as the Hu-Hwang-Wang conjecture.
↑ The number of tests, $t$ , must scale as $t=O\left({\frac {d^{2}\log n}{\log d}}\right)$ for deterministic designs, compared to $t=O(d\log n)$ for designs that allow arbitrarily small probabilities of error (as $d\to \infty$ and $n\to \infty$ ).^[4]
↑ We must be careful to distinguish between when a test reports a false result and when the group-testing procedure fails as a whole. It is both possible to make an error with no incorrect tests and to not make an error with some incorrect tests.
↑ In fact we can do much better. For example, Li's $s$ -stage algorithm gives an explicit construction were $t\leq {\frac {e}{\log _{2}e}}d\log _{2}{(n/d)}$ .
↑ Alternatively we can define $\mathbf {y}$ by the equation $\mathbf {y} :=M\mathbf {x}$ , where multiplication is logical AND ( $\wedge$ ) and addition is logical OR ( $\vee$ ). Here, $\mathbf {y}$ will have a $1$ in position $i$ if and only if $(M)_{i,j}$ and $\mathbf {x} _{j}$ are both $1$ for any $j$ . That is, if and only if at least one defective item was included in the $i{\textrm {-th}}$ test.
↑ This kind of measurement comes up in many applications. For example, certain kinds of digital camera^[27] or MRI machines,^[28] where time constraints force us to take a small number of measurements.
↑ More formally hashes have a property called collision resistance, which is that the likelihood of the same hash resulting from different inputs is very low for data of an appropriate size. In practice, the chance that two different inputs might produce the same hash is often ignored.

References

Citations

↑ Colbourn, Charles J.; Dinitz, Jeffrey H. (2007), Handbook of Combinatorial Designs (2nd ed.), Boca Raton: Chapman & Hall/ CRC, p. 574, Section 46: Pooling Designs, ISBN 1-58488-506-8
1 2 Dorfman, Robert (December 1943), "The Detection of Defective Members of Large Populations", The Annals of Mathematical Statistics, 14 (4): 436–440, JSTOR 2235930, doi:10.1214/aoms/1177731363
1 2 3 4 5 6 7 8 9 10 11 12 13 Ding-Zhu, Du; Hwang, Frank K. (1993). Combinatorial group testing and its applications. Singapore: World Scientific. ISBN 9810212933.
1 2 3 4 5 6 Atia, George Kamal; Saligrama, Venkatesh (March 2012). "Boolean compressed sensing and noisy group testing". IEEE Transactions on Information Theory. 58 (3): 1880–1901. arXiv:0907.1061 . doi:10.1109/TIT.2011.2178156.
↑ Chen, Hong-Bin; Fu, Hung-Lin (April 2009). "Nonadaptive algorithms for threshold group testing". Discrete Applied Mathematics. 157 (7): 1581–1585. doi:10.1016/j.dam.2008.06.003.
↑ De Bonis, Annalisa (20 July 2007). "New combinatorial structures with applications to efficient group testing with inhibitors". Journal of Combinatorial Optimization. 15 (1): 77–94. doi:10.1007/s10878-007-9085-1.
↑ Hayes, J. (August 1978). "An adaptive technique for local distribution". IEEE Transactions on Communications. 26 (8): 1178–1186. doi:10.1109/TCOM.1978.1094204.
↑ Sterrett, Andrew (December 1957). "On the detection of defective members of large populations". The Annals of Mathematical Statistics. 28 (4): 1033–1036. doi:10.1214/aoms/1177706807.
↑ Sobel, Milton;; Groll, Phyllis A. (September 1959). "Group testing to eliminate efficiently all defectives in a binomial sample". Bell System Technical Journal. 38 (5): 1179–1252. doi:10.1002/j.1538-7305.1959.tb03914.x.
↑ Li, Chou Hsiung (June 1962). "A sequential method for screening experimental variables". Journal of the American Statistical Association. 57 (298): 455–477. doi:10.1080/01621459.1962.10480672.
↑ Katona, Gyula O.H. (1973). "A survey of combinatorial theory". Combinatorial search problems. North-Holland, Amsterdam: 285–308.
1 2 3 4 Hwang, Frank K. (September 1972). "A method for detecting all defective members in a population by group testing". Journal of the American Statistical Association. 67 (339): 605–608. JSTOR 2284447. doi:10.2307/2284447.
↑ Allemann, Andreas (2013). "An efficient algorithm for combinatorial group testing". Information Theory, Combinatorics, and Search Theory. Springer Berlin Heidelberg: 569–596.
1 2 Hu, M. C.; Hwang, F. K.; Wang, Ju Kwei (June 1981). "A Boundary Problem for Group Testing". SIAM Journal on Algebraic Discrete Methods. 2 (2): 81–87. doi:10.1137/0602011.
↑ Leu, Ming-Guang (28 October 2008). "A note on the Hu–Hwang–Wang conjecture for group testing.". The ANZIAM Journal. 49 (4): 561. doi:10.1017/S1446181108000175.
↑ Riccio, Laura; Colbourn, Charles J. (1 January 2000). "Sharper bounds in adaptive group testing". Taiwanese Journal of Mathematics. 4 (4): 669–673.
1 2 3 4 5 6 7 Chun Lam Chan; Pak Hou Che; Jaggi, Sidharth; Saligrama, Venkatesh (1 September 2011), "Non-adaptive probabilistic group testing with noisy measurements: near-optimal bounds with efficient algorithms", 49th Annual Allerton Conference on Communication, Control, and Computing, pp. 1832–1839, arXiv:1107.4540  [cs.IT], doi:10.1109/Allerton.2011.6120391
1 2 3 Aldridge, Matthew; Baldassini, Leonardo; Johnson, Oliver (June 2014). "Group Testing Algorithms: Bounds and Simulations". IEEE Transactions on Information Theory. 60 (6): 3671–3687. doi:10.1109/TIT.2014.2314472.
↑ Baldassini, L.; Johnson, O.; Aldridge, M. (1 July 2013), "The capacity of adaptive group testing", IEEE International Symposium on Information Theory, pp. 2676–2680, doi:10.1109/ISIT.2013.6620712
↑ Sobel, Milton; Elashoff, R. M. (1975). "Group testing with a new goal, estimation". Biometrika. 62 (1): 181–193. doi:10.1093/biomet/62.1.181.
↑ Bar-Noy, A.; Hwang, F. K.; Kessler, I.; Kutten, S. (1 May 1992). "A new competitive algorithm for group testing". Eleventh Annual Joint Conference of the IEEE Computer and Communications Societies. Institute of Electrical and Electronics Engineers. 2: 786–793. doi:10.1109/INFCOM.1992.263516.
↑ Damaschke, Peter (2000). "Adaptive versus nonadaptive attribute-efficient learning". Machine Learning. 41 (2): 197–215. doi:10.1023/A:1007616604496.
↑ Stinson, D. R.; van Trung, Tran; Wei, R (May 2000). "Secure frameproof codes, key distribution patterns, group testing algorithms and related structures". Journal of Statistical Planning and Inference. 86 (2): 595–617. doi:10.1016/S0378-3758(99)00131-7.
↑ Colbourn, C. J.; Dinitz, J. H.; Stinson, D. R. (1999). "Communications, Cryptography, and Networking". Surveys in Combinatorics (267): 37.
↑ Goodrich, Michael T.; Atallah, Mikhail J.; Tamassia, Roberto (7 June 2005). "Indexing information for data forensics". Applied Cryptography and Network Security. Springer Berlin Heidelberg: 206–221. doi:10.1007/11496137_15.
↑ Chlebus, B. S. (2001). "Randomized communication in radio networks". In: Pardalos, P. M.; Rajasekaran, S.; Reif, J.; Rolim, J. D. P. (Eds.), Handbook of Randomized Computing, Vol. I, p.401–456. Kluwer Academic Publishers, Dordrecht.
↑ Takhar, D.; Laska, J. N.; Wakin, M. B.; Duarte, M. F.; Baron, D.; Sarvotham, S.; Kelly, K. F.; Baraniuk, R. G. (February 2006). "A new compressive imaging camera architecture using optical-domain compression". Electronic Imaging. International Society for Optics and Photonics: 606509–606509.
↑ Candès, E. J. (2014). "Mathematics of sparsity (and a few other things)". Proceedings of the International Congress of Mathematicians. Seoul, South Korea.
1 2 Gilbert, A. C.; Iwen, M. A.; Strauss, M. J. (October 2008). "Group testing and sparse signal recovery". 42nd Asilomar Conference on Signals, Systems and Computers: 1059–1063. Institute of Electrical and Electronics Engineers.
↑ Wright, S. J.; Nowak, R. D.; Figueiredo, M. A. T. (July 2009). "Sparse Reconstruction by Separable Approximation". IEEE Transactions on Signal Processig. 57 (7): 2479–2493. doi:10.1109/TSP.2009.2016892.
1 2 Berinde, R.; Gilbert, A. C.; Indyk, P.; Karloff, H.; Strauss, M. J. (September 2008). "Combining geometry and combinatorics: A unified approach to sparse signal recovery". 46th Annual Allerton Conference on Communication, Control, and Computing. Institute of Electrical and Electronics Engineers: 798–805. doi:10.1109/ALLERTON.2008.4797639.
↑ Indyk, Piotr (1 January 2008). "Explicit Constructions for Compressed Sensing of Sparse Signals". Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics: 30–33.

General references

Ding-Zhu, Du; Hwang, Frank K. (1993). Combinatorial group testing and its applications. Singapore: World Scientific. ISBN 9810212933.
Atri Rudra's course on Error Correcting Codes: Combinatorics, Algorithms, and Applications (Spring 2007), Lectures 7.
Atri Rudra's course on Error Correcting Codes: Combinatorics, Algorithms, and Applications (Spring 2010), Lectures 10, 11, 28, 29
Du, D., & Hwang, F. (2006). Pooling Designs and Nonadaptive Group Testing. Boston: Twayne Publishers.
Ely Porat, Amir Rothschild: Explicit Non-adaptive Combinatorial Group Testing Schemes. ICALP (1) 2008: 748-759
Kagan, Eugene; Ben-gal, Irad (2014), "A group testing algorithm with online informational learning", IIE Transactions, 46: 164–184, ISSN 0740-817X, doi:10.1080/0740817X.2013.803639
Goodrich, Michael T.; Atallah, Mikhail J.; Tamassia, Roberto (7 June 2005). "Indexing information for data forensics". Applied Cryptography and Network Security. Springer Berlin Heidelberg: 206–221. doi:10.1007/11496137_15.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.