Great rhombihexahedron

Great rhombihexahedron
Type	Uniform star polyhedron
Elements	F = 18, E = 48 V = 24 (χ = −6)
Faces by sides	12{4}+6{8/3}
Wythoff symbol	2 4/3 (3/2 4/2) |
Symmetry group	Oh, [4,3], *432
Index references	U21, C82, W103
Dual polyhedron	Great rhombihexacron
Vertex figure	4.8/3.4/3.8/5
Bowers acronym	Groh

In geometry, the great rhombihexahedron is a nonconvex uniform polyhedron, indexed as U₂₁. Its dual is the great rhombihexacron.^[1] Its vertex figure is a crossed quadrilateral.

Orthogonal projections

Filling

There is some controversy on how to colour the faces of this polyhedron. Although the common way to fill in a polygon is to just colour its whole interior, this can result in some filled regions hanging as membranes over empty space. Hence, the "neo filling" is sometimes used instead as a more accurate filling. In the neo filling, orientable polyhedra are filled traditionally, but non-orientable polyhedra have their faces filled with the modulo-2 method (only odd-density regions are filled in).^[2]

Traditional filling

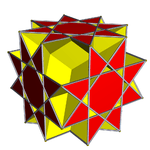"Neo filling"

Related polyhedra

It shares the vertex arrangement with the convex truncated cube. It additionally shares its edge arrangement with the nonconvex great rhombicuboctahedron (having 12 square faces in common), and with the great cubicuboctahedron (having the octagrammic faces in common).

Truncated cube

Nonconvex great rhombicuboctahedron

Great cubicuboctahedron

Great rhombihexahedron

It may be constructed as the exclusive or (blend) of three octagrammic prisms.

Great rhombihexacron

Great rhombihexacron
Type	Star polyhedron
Face
Elements	F = 24, E = 48 V = 18 (χ = −6)
Symmetry group	Oh, [4,3], *432
Index references	DU21
dual polyhedron	Great rhombihexahedron

The great rhombihexacron is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron (U₂₁).^[3] It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges.^[4]

It has 12 outer vertices which have the same vertex arrangement as the cuboctahedron, and 6 inner vertices with the vertex arrangement of an octahedron.

As a surface geometry, it can be seen as visually similar to a Catalan solid, the disdyakis dodecahedron, with much taller rhombus-based pyramids joined to each face of a rhombic dodecahedron.

See also

• List of uniform polyhedra

References

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 
• uniform polyhedra and duals

External links

• Weisstein, Eric Wolfgang. "Great rhombihexahedron". MathWorld.