Good spanning tree

Conditions of good spanning tree

In the mathematical field of graph theory, a good spanning tree ^[1] $T$ of an embedded planar graph $G$ is a rooted spanning tree of $G$ whose non-tree edges satisfy the following conditions.

there is no non-tree edge $(u,v)$ where $u$ and $v$ lie on a path from the root of $T$ to a leaf,
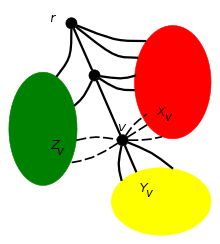
the edges incident to a vertex $v$ can be divided by three sets $X_{v},Y_{v}$ and $Z_{v}$ , where,
- $X_{v}$ is a set of non-tree edges, they terminate in red zone
- $Y_{v}$ is a set of tree edges, they are children of $v$
- $Z_{v}$ is a set of non-tree edges, they terminate in green zone

Formal definition^[1]^[2]

An illustration for

X_{v},Y_{v}

and

Z_{v}

sets of edges

Let $G_\phi$ be a plane graph. Let $T$ be a rooted spanning tree of $G_\phi$ . Let $P(r,v)=(r=u_{1}),u_{2},\ldots ,(v=u_{k})$ be the path in $T$ from the root $r$ to a vertex $v\neq r$ . The path $P(r,v)$ divides the children of $u_{i}$ , $(1\leq i<k)$ , except $u_{i+1}$ , into two groups; the left group $L$ and the right group $R$ . A child $x$ of $u_{i}$ is in group $L$ and denoted by $u_{i}^{L}$ if the edge $(u_{i},x)$ appears before the edge $(u_{i},u_{i+1})$ in clockwise ordering of the edges incident to $u_{i}$ when the ordering is started from the edge $(u_{i},u_{i+1})$ . Similarly, a child $x$ of $u_{i}$ is in the group $R$ and denoted by $u_{i}^{R}$ if the edge $(u_{i},x)$ appears after the edge $(u_{i},u_{i+1})$ in clockwise order of the edges incident to $u_{i}$ when the ordering is started from the edge $(u_{i},u_{i+1})$ . The tree $T$ is called a good spanning tree^[1] of $G_\phi$ if every vertex $v$ $(v\neq r)$ of $G_\phi$ satisfies the following two conditions with respect to $P(r,v)$ .

[Cond1] $G_\phi$ does not have a non-tree edge $(v,u_{i})$ , $i<k$ ; and
[Cond2] the edges of $G_\phi$ incident to the vertex $v$ excluding $(u_{k-1},v)$ can be partitioned into three disjoint (possibly empty) sets $X_{v},Y_{v}$ and $Z_{v}$ satisfying the following conditions (a)-(c)
- (a) Each of $X_{v}$ and $Z_{v}$ is a set of consecutive non-tree edges and $Y_{v}$ is a set of consecutive tree edges.
- (b) Edges of set $X_{v}$ , $Y_{v}$ and $Z_{v}$ appear clockwise in this order from the edge $(u_{k-1},v)$ .
- (c) For each edge $(v,v')\in X_{v}$ , $v'$ is contained in $T_{u_{i}^{L}}$ , $i<k$ , and for each edge $(v,v')\in Z_{v}$ , $v'$ is contained in $T_{u_{i}^{R}}$ , $i<k$ .
  A plane graph $G_\phi$ (top), a good spanning tree $T$ of $G_\phi$ (down) solid edges are part of good spanning tree and dotted edges are non-tree edges in $G_\phi$ with respect to $T$ .

Applications

In monotone drawing of graphs,^[3] in 2-visibility representation of graphs.^[1]

Finding good spanning tree

Every planar graph $G$ has an embedding $G_\phi$ such that $G_\phi$ contains a good spanning tree. A good spanning tree and a suitable embedding can be found from $G$ in linear-time.^[1] Not all embeddings of $G$ contain a good spanning tree.

References

1 2 3 4 5 Hossain, Md. Iqbal; Rahman, Md. Saidur (23 November 2015). "Good spanning trees in graph drawing". Theoretical Computer Science. 607: 149–165. doi:10.1016/j.tcs.2015.09.004.
↑ Hossain, Md Iqbal; Rahman, Md Saidur (22 October 2013). "Monotone Grid Drawings of Planar Graphs". arXiv:1310.6084 [cs].
↑ Hossain, Md Iqbal; Rahman, Md Saidur (28 June 2014). "Monotone Grid Drawings of Planar Graphs". Frontiers in Algorithmics. Springer, Cham: 105–116. doi:10.1007/978-3-319-08016-1_10.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Good spanning tree

Formal definition[1][2]

Applications

Finding good spanning tree

See also

References

Formal definition^[1]^[2]