Trigonal trapezohedron
| Trigonal trapezohedron | |
|---|---|
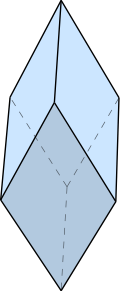 Click on picture for large version. | |
| Type | trapezohedra |
| Conway notation | dA3 |
| Coxeter diagram | |
| Faces | 6 rhombi |
| Edges | 12 |
| Vertices | 8 |
| Face configuration | 3,3,3,3 |
| Symmetry group | D3d, [2+,6], (2*3), order 12 |
| Rotation group | D3, [2,3]+, (223), order 6 |
| Dual polyhedron | trigonal antiprism |
| Properties | convex, face-transitive |
In geometry, a trigonal trapezohedron or trigonal deltohedron is a three-dimensional figure formed by six congruent rhombi.
Six identical rhombic faces can construct two configurations of trigonal trapezohedra. The acute or prolate form has three acute angles corners of the rhombic faces meeting at two polar axis vertices. The obtuse or oblate or flat form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices.
The trigonal trapezohedra is a special case of a rhombohedron. A general rhombohedron allows up to three types of rhombic faces.
Geometry
A trigonal trapezohedron is a special kind of parallelepiped, and are the only parallelepipeds with six congruent faces. Since all of the edges must have the same length, every trigonal trapezohedron is also a rhombohedron.
It is the simplest of the trapezohedra, an infinite sequence of polyhedra which are dual to the antiprisms. The dual of a trigonal trapezohedron is a triangular antiprism.
 A trigonal trapezohedron with square faces is a cube.
A trigonal trapezohedron with square faces is a cube.
Asymmetric variation
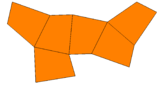
A lower symmetry variation of the trigonal trapezohedron has only rotational symmetry, D3, and is made from 6 identical irregular quadrilaterals.[1]
| Polar axis | Side | Net |
|---|---|---|
 |
 |
 |
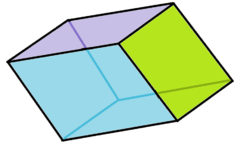
Golden rhombohedron
 Acute form |
 Obtuse form |
A golden rhombohedron is one of two special case of the trigonal trapezohedron with golden rhombus faces. The acute or prolate form has three acute angles corners of the rhombic faces meeting at two polar axis vertices. The obtuse or oblate or flat form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices. Cartesian coordinates for a golden rhombohedron with one pole at the origin are:
- (0,0,0)
- (1,0,0)
- (1/√5, 2/√5, 0)
- (1/2, φ − 1/2, φ/2)
and vector additions thereof, where φ = √5 + 1/2 is the golden ratio.
The rhombic hexecontahedron can be constructed by 20 acute golden rhombohedra meeting at a point.
Related polyhedra
A regular octahedron augumented by 2 regular tetrahedra creates a trigonal trapezohedron, with coplanar equilateral triangles merged into 60-degree rhombic faces.
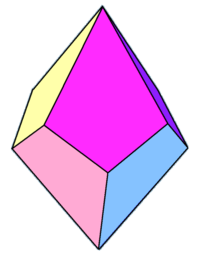
| Family of trapezohedra V.n.3.3.3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron |  |
 |
 |
 |
 |
 |
 |
 |
||
| Tiling |  |
 |
 |
 |
 |
 |
 |
 |
||
| Config. | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | ...V10.3.3.3 | ...V12.3.3.3 | ...V∞.3.3.3 |
