Free-orbit experiment with laser interferometry X-rays

The Free-orbit Experiment with Laser Interferometry X-Rays (FELIX)[1] belongs to a category of experiments exploring whether macroscopic systems can be in superposition states. It was originally proposed by the physicist Roger Penrose in his book The Road to Reality specifically to prove whether unconventional decoherence processes such as gravitationally induced decoherence or spontaneous wave-function collapse of a quantum system occur.

Later revised to take place as a tabletop experiment,[2][3] if successful, it is estimated that a mass of roughly 1014 atoms would have been superposed, approximately nine orders of magnitude more massive than any superposition observed to that date (2003).

Configuration

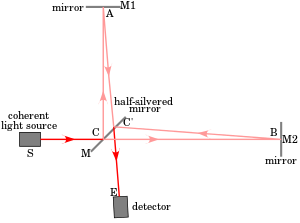
Figure 2. A Michelson interferometer.

The proposed experimental setup is basically a variation of the Michelson interferometer but for a single photon. Additionally, one of the mirrors has to be very tiny and fixed on an isolated micromechanical-oscillator. This allows it to move when the photon is reflected on it, so that it may become superposed with the photon. The purpose is to vary the size of the mirror to investigate the effect of the mass on the time it takes for the quantum system to collapse.

Originally the arms of the interferometer had to stretch into the hundreds of thousands of kilometers to achieve a photon roundtrip-time comparable to the oscillator's period, but that meant that the experiment had to take place in-orbit, reducing its viability. The revised proposal[2] requires that the mirrors be placed into high-finesse optical cavities that will trap the photons long enough to achieve the desired delay.

There are various technological challenges, but all are within high-end laboratory capabilities. The primary requirement is that the mass of the cavity remains as small as possible. To avoid noise on the interferometer and have a low probability of emitting more than one photon each time, a very low absolute temperature for the experiment is needed, on the order of 60 μK. For similar reasons, and to avoid decoherence, the experimental device has to be in ultra-high vacuum conditions. The wavelength of the photons was calculated to be roughly 630 nm so the reflecting surfaces can be as small as possible and yet avoid refraction and reflectivity issues. The micromechanical-oscillator can be similar to the cantilevers in atomic force microscopy and the reflective surfaces typically used in similar high-demanding experiments pose no real challenge. Various elaborate electromagnetic mechanisms have been proposed to "reset" the cavities to a stable state before each repetition of the experiment.

See also

References

  1. ↑ Penrose, Roger (Dec 2002) [2000]. Gravitational Collapse of the Wavefunction: AN Experimentally Testable Proposal (PDF). THE NINTH MARCEL GROSSMANN MEETING On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories. Proceedings of the MGIX MM Meeting. Held 2–8 July 2000 in The University of Rome "La Sapienza", Italy. World Scientific Publishing Co. Pte. Ltd. pp. 3–6. ISBN 9789812777386. doi:10.1142/9789812777386_0001. Retrieved 21 June 2014.
  2. 1 2 Marshall, William; Christoph, Simon; Penrose, Roger; Bouwmeester, Dik (Sep 2003). "Towards quantum superpositions of a mirror". Physical Review Letters. American Physical Society. 91 (13): 130401–130405. Bibcode:2003PhRvL..91m0401M. PMID 14525288. arXiv:quant-ph/0210001 Freely accessible. doi:10.1103/PhysRevLett.91.130401.
  3. ↑ Adler, Stephen; Bassi, Angelo; Ippoliti, Emiliano (9 March 2005). "Towards quantum superpositions of a mirror: an exact open systems analysis—calculational details". Journal of Physics A: Mathematical and General. IOP Publishing Ltd. 38 (12): 2715–2727. Bibcode:2005JPhA...38.2715A. arXiv:quant-ph/0407084 Freely accessible. doi:10.1088/0305-4470/38/12/013.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.