Flood fill
.gif)
Flood fill, also called seed fill, is an algorithm that determines the area connected to a given node in a multi-dimensional array. It is used in the "bucket" fill tool of paint programs to fill connected, similarly-colored areas with a different color, and in games such as Go and Minesweeper for determining which pieces are cleared. When applied on an image to fill a particular bounded area with color, it is also known as boundary fill.
The algorithm
.gif)
The flood-fill algorithm takes three parameters: a start node, a target color, and a replacement color. The algorithm looks for all nodes in the array that are connected to the start node by a path of the target color and changes them to the replacement color. There are many ways in which the flood-fill algorithm can be structured, but they all make use of a queue or stack data structure, explicitly or implicitly.
Depending on whether we consider nodes touching at the corners connected or not, we have two variations: eight-way and four-way respectively.
Stack-based recursive implementation (four-way)
One implicitly stack-based (recursive) flood-fill implementation (for a two-dimensional array) goes as follows:
Flood-fill (node, target-color, replacement-color):
1. If target-color is equal to replacement-color, return.
2. If the color of node is not equal to target-color, return.
3. Set the color of node to replacement-color.
4. Perform Flood-fill (one step to the south of node, target-color, replacement-color).
Perform Flood-fill (one step to the north of node, target-color, replacement-color).
Perform Flood-fill (one step to the west of node, target-color, replacement-color).
Perform Flood-fill (one step to the east of node, target-color, replacement-color).
5. Return.
Though easy to understand, the implementation of the algorithm used above is impractical in languages and environments where stack space is severely constrained (e.g. Java applets).
Alternative implementations
An explicitly queue-based implementation (sometimes called "Forest Fire algorithm"[1]) is shown in pseudo-code below. It is similar to the simple recursive solution, except that instead of making recursive calls, it pushes the nodes onto a queue for consumption:
Flood-fill (node, target-color, replacement-color):
1. If target-color is equal to replacement-color, return.
2. If color of node is not equal to target-color, return.
3. Set Q to the empty queue.
4. Set the color of node to replacement-color.
5. Add node to the end of Q.
6. While Q is not empty:
7. Set n equal to the first element of Q.
8. Remove first element from Q.
9. If the color of the node to the west of n is target-color,
set the color of that node to replacement-color and add that node to the end of Q.
10. If the color of the node to the east of n is target-color,
set the color of that node to replacement-color and add that node to the end of Q.
11. If the color of the node to the north of n is target-color,
set the color of that node to replacement-color and add that node to the end of Q.
12. If the color of the node to the south of n is target-color,
set the color of that node to replacement-color and add that node to the end of Q.
13. Return.
Most practical implementations use a loop for the west and east directions as an optimization to avoid the overhead of stack or queue management:
Flood-fill (node, target-color, replacement-color): 1. If target-color is equal to replacement-color, return. 2. If color of node is not equal to target-color, return. 3. Set Q to the empty queue. 4. Add node to Q. 5. For each element N of Q: 6. Set w and e equal to N. 7. Move w to the west until the color of the node to the west of w no longer matches target-color. 8. Move e to the east until the color of the node to the east of e no longer matches target-color. 9. For each node n between w and e: 10. Set the color of n to replacement-color. 11. If the color of the node to the north of n is target-color, add that node to Q. 12. If the color of the node to the south of n is target-color, add that node to Q. 13. Continue looping until Q is exhausted. 14. Return.
Adapting the algorithm to use an additional array to store the shape of the region allows generalization to cover "fuzzy" flood filling, where an element can differ by up to a specified threshold from the source symbol. Using this additional array as an alpha channel allows the edges of the filled region to blend somewhat smoothly with the not-filled region.
Fixed-memory method (right-hand fill method)
A method exists that uses essentially no memory for four-connected regions by pretending to be a painter trying to paint the region without painting himself into a corner. This is also a method for solving mazes. The four pixels making the primary boundary are examined to see what action should be taken. The painter could find themselves in one of several conditions:
- All four boundary pixels are filled.
- Three of the boundary pixels are filled.
- Two of the boundary pixels are filled.
- One boundary pixel is filled.
- Zero boundary pixels are filled.
Where a path or boundary is to be followed, the right-hand rule is used. The painter follows the region by placing their right-hand on the wall (the boundary of the region) and progressing around the edge of the region without removing their hand.
For case #1, the painter paints (fills) the pixel the painter is standing upon and stops the algorithm.
For case #2, a path leading out of the area exists. Paint the pixel the painter is standing upon and move in the direction of the open path.
For case #3, the two boundary pixels define a path which, if we painted the current pixel, may block us from ever getting back to the other side of the path. We need a "mark" to define where we are and which direction we are heading to see if we ever get back to exactly the same pixel. If we already created such a "mark", then we preserve our previous mark and move to the next pixel following the right-hand rule.
A mark is used for the first 2-pixel boundary that is encountered to remember where the passage started and in what direction the painter was moving. If the mark is encountered again and the painter is traveling in the same direction, then the painter knows that it is safe to paint the square with the mark and to continue in the same direction. This is because (through some unknown path) the pixels on the other side of the mark can be reached and painted in the future. The mark is removed for future use.
If the painter encounters the mark but is going in a different direction, then some sort of loop has occurred, which caused the painter to return to the mark. This loop must be eliminated. The mark is picked up, and the painter then proceeds in the direction indicated previously by the mark using a left-hand rule for the boundary (similar to the right-hand rule but using the painter's left hand). This continues until an intersection is found (with three or more open boundary pixels). Still using the left-hand rule the painter now searches for a simple passage (made by two boundary pixels). Upon finding this two-pixel boundary path, that pixel is painted. This breaks the loop and allows the algorithm to continue.
For case #4, we need to check the opposite 8-connected corners to see whether they are filled or not. If either or both are filled, then this creates a many-path intersection and cannot be filled. If both are empty, then the current pixel can be painted and the painter can move following the right-hand rule.
The algorithm trades time for memory. For simple shapes it is very efficient. However, if the shape is complex with many features, the algorithm spends a large amount of time tracing the edges of the region trying to ensure that all can be painted.
This algorithm was first available commercially in 1981 on a Vicom Image Processing system manufactured by Vicom Systems, Inc. The classic recursive flood fill algorithm was available on this system as well.
Pseudocode
This is a pseudocode implementation of an optimal fixed-memory flood-fill algorithm written in structured English:
The variables:
cur, mark, and mark2 each hold either pixel coordinates or a null value
NOTE: when mark is set to null, do not erase its previous coordinate value.
Keep those coordinates available to be recalled if necessary.
cur-dir, mark-dir, and mark2-dir each hold a direction (left, right, up, or down)
backtrack and findloop each hold boolean values
count is an integer
The algorithm:
(NOTE: All directions (front, back, left, right) are relative to cur-dir)
set cur to starting pixel set cur-dir to default direction clear mark and mark2 (set values to null) set backtrack and findloop to false while front-pixel is empty move forward end while jump to START MAIN LOOP: move forward if right-pixel is empty if backtrack is true and findloop is false and either front-pixel or left-pixel is empty set findloop to true end if turn right PAINT: move forward end if START: set count to number of non-diagonally adjacent pixels filled (front/back/left/right ONLY) if count is not 4 do turn right while front-pixel is empty do turn left while front-pixel is filled end if switch count case 1 if backtrack is true set findloop to true else if findloop is true if mark is null restore mark end if else if front-left-pixel and back-left-pixel are both empty clear mark fill cur jump to PAINT end if end case case 2 if back-pixel is filled if front-left-pixel is not filled clear mark fill cur jump to PAINT end if else if mark is not set set mark to cur set mark-dir to cur-dir clear mark2 set findloop and backtrack to false else if mark2 is not set if cur is at mark if cur-dir is the same as mark-dir clear mark turn around fill cur jump to PAINT else set backtrack to true set findloop to false set cur-dir to mark-dir end if else if findloop is true set mark2 to cur set mark2-dir to cur-dir end if else if cur is at mark set cur to mark2 set cur-dir to mark2-dir clear mark and mark2 set backtrack to false turn around fill cur jump to PAINT else if cur at mark2 set mark to cur set cur-dir and mark-dir to mark2-dir clear mark2 end end if end if end case case 3 clear mark fill cur jump to PAINT end case case 4 fill cur done end case end switch end MAIN LOOP
Scanline fill

The algorithm can be sped up by filling lines. Instead of pushing each potential future pixel coordinate on the stack, it inspects the neighbour lines (previous and next) to find adjacent segments that may be filled in a future pass; the coordinates (either the start or the end) of the line segment are pushed on the stack. In most cases this scanline algorithm is at least an order of magnitude faster than the per-pixel one.
Efficiency: each pixel is checked once.
Vector implementations
Version 0.46 of Inkscape includes a bucket fill tool, giving output similar to ordinary bitmap operations and indeed using one: the canvas is rendered, a flood fill operation is performed on the selected area and the result is then traced back to a path. It uses the concept of a boundary condition.
Large-scale behaviour
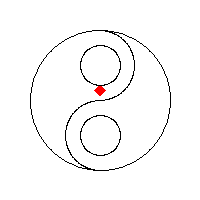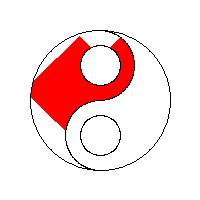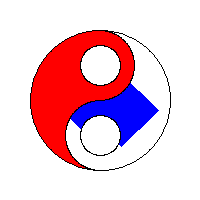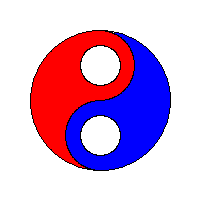
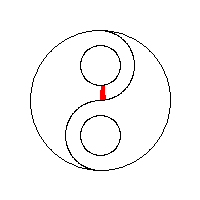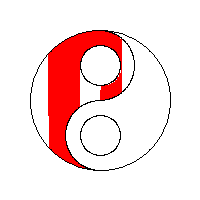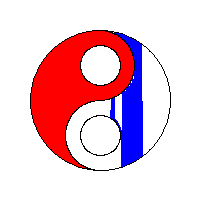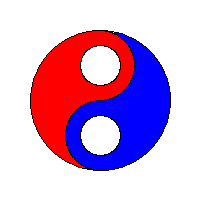
The primary technique used to control a flood fill will either be data-centric or process-centric. A data-centric approach can use either a stack or a queue to keep track of seed pixels that need to be checked. A process-centric algorithm must necessarily use a stack.
A 4-way flood-fill algorithm that uses the adjacency technique and a queue as its seed pixel store yields an expanding lozenge-shaped fill.
Efficiency: 4 pixels checked for each pixel filled (8 for an 8-way fill).
A 4-way flood-fill algorithm that use the adjacency technique and a stack as its seed pixel store yields a linear fill with "gaps filled later" behaviour. This approach can be particularly seen in older 8-bit computer games, such as those created with Graphic Adventure Creator.
Efficiency: 4 pixels checked for each pixel filled (8 for an 8-way fill).
See also
- Breadth-first search
- Depth-first search
- Graph traversal
- Connected-component labeling
- Dijkstra's algorithm
External links
- Didactical Javascript implementation of scanline polygon fill, by Guilherme Polo.
- Sample implementations for recursive and non-recursive, classic and scanline flood fill, by Lode Vandevenne.
- Flash flood fill implementation, by Emanuele Feronato.
- QuickFill: An efficient flood fill algorithm., by John R. Shaw.
References
- ↑ Torbert, Shane (2016). Applied Computer Science (2nd ed.). Springer (published 2016-06-01). p. 158. ISBN 978-3-319-30864-7. LCCN 2016936660. doi:10.1007/978-3-319-30866-1.