Exsecant

The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astronomy, and spherical trigonometry and could help improve accuracy, but are rarely used today except to simplify some calculations.

A unit circle with trigonometric functions.

Exsecant

The trigonometric functions, including the exsecant, can be constructed geometrically in terms of a unit circle centered at O. The exsecant is the portion DE of the secant exterior to (ex) the circle.

The exsecant,[1][2][3][4][5][6][7] (Latin: secans exterior[8][9][10][11]) also known as exterior, external,[12][13][14] outward or outer secant and abbreviated as exsec[1][15][5][6][7][12][13][16][17][18] or exs,[19] is a trigonometric function defined in terms of the secant function sec(θ):[5][18][20]

[5][6][7][12][13][16][17][18][20]

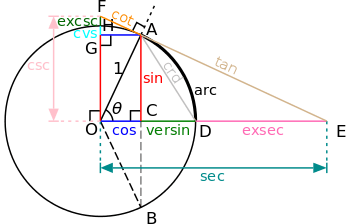
The name exsecant can be understood from a graphical construction of the various trigonometric functions from a unit circle, such as was used historically. sec(θ) is the secant line OE, and the exsecant is the portion DE of this secant that lies exterior to the circle (ex is Latin for out of).

Excosecant

exsecant (blue) and excosecant (green)

A related function is the excosecant[21][22] or coexsecant,[23][15][24] also known as exterior, external,[14] outward or outer cosecant and abbreviated as excosec, coexsec,[15][24] excsc[21][22] or exc,[19] the exsecant of the complementary angle:

[22]

Usage

Important in fields such as surveying,[6] railway engineering[21] (for example to lay out railroad curves and superelevation), civil engineering, astronomy, and spherical trigonometry up into the 1980s, the exsecant function is now little-used.[6][20] Mainly, this is because the broad availability of calculators and computers has removed the need for trigonometric tables of specialized functions such as this one.[6]

The reason to define a special function for the exsecant is similar to the rationale for the versine: for small angles θ, the sec(θ) function approaches one, and so using the above formula for the exsecant will involve the subtraction of two nearly equal quantities, resulting in catastrophic cancellation. Thus, a table of the secant function would need a very high accuracy to be used for the exsecant, making a specialized exsecant table useful. Even with a computer, floating point errors can be problematic for exsecants of small angles, if using the cosine-based definition. A more accurate formula in this limit would be to use the identity:

[2][3][14]

or

[14]

Prior to the availability of computers, this would require time-consuming multiplications.

The exsecant function was used by Galileo Galilei in 1632 already, although he still called it segante (meaning secant).[25][26][27][28] The Latin term secans exterior was used since at least around 1745.[8][9][10][11] The usage of the English term exsecant can be traced back to 1894 the least.[1]

The English term coexsecant can be found used as early as 1903[23] followed by excosecant since 1909.[21] The function was also utilized by Albert Einstein to describe the kinetic energy of fermions.[27][28]

Mathematical identities

Derivatives

[18]

Integrals

[18]

Inverse functions

The inverse functions arcexsecant[24] (arcexsec,[24] aexsec,[29][30] aexs, exsec−1) and arcexcosecant (arcexcosec, arcexcsc, aexcsc, aexc, arccoexsecant (arccoexsec, excsc−1) exist as well:

[24][29][30] (for y ≤ −2 or y ≥ 0)[24]

Other properties

Derived from the unit circle:

The exsecant function is related to the tangent function by

[20]

In analogy, the excosecant function is related to the cotangent function by

The exsecant function is related to the sine function by

In analogy, the excosecant function is related to the cosine function by

[28]

The exsecant and excosecant functions can be extended into the complex plane.[18]

See also

References

  1. 1 2 3 Allen, Calvin Frank (1894) [1889]. Railroad Curves and Earthwork. New York, USA; London, UK: Spon & Chamberlain; E. & F. Spon, Ltd. Retrieved 2015-11-16.
  2. 1 2 Nagle, James C. (1897). "IV.138.-165.: Transition Curves; Table XIII.: Natural Versines and Exsecants". Field Manual for Railroad Engineers (1 ed.). New York, USA: John Wiley and Sons, Chapman and Hall, Limited. pp. 110–142;332–354. Retrieved 2015-11-16.
  3. 1 2 "Field Manual for Railroad Engineers" (PDF). The Engineer (Review): 540. 1897-12-03. Archived (PDF) from the original on 2015-11-17. Retrieved 2015-11-17.
  4. ↑ Boyer, Carl Benjamin (1969) [1959]. "5: Commentary on the Paper of E. J. Dijksterhuis (The Origins of Classical Mechanics from Aristotle to Newton)". In Clagett, Marshall. Critical Problems in the History of Science (3 ed.). Madison, Milwaukee, and London: University of Wisconsin Press, Ltd. pp. 185–190. ISBN 0-299-01874-1. LCCN 59-5304. 9780299018740. Retrieved 2015-11-16.
  5. 1 2 3 4 Zucker, Ruth (1983) [June 1964]. "Chapter 4.3.147: Elementary Transcendental Functions - Circular functions". In Abramowitz, Milton; Stegun, Irene Ann. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 78. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
  6. 1 2 3 4 5 6 Calvert, James B. (2007-09-14) [2004-01-10]. "Trigonometry". Archived from the original on 2007-10-02. Retrieved 2015-11-08.
  7. 1 2 3 Tapson, Frank (2004). "Background Notes on Measures: Angles". 1.4. Cleave Books. Archived from the original on 2007-02-09. Retrieved 2015-11-12.
  8. 1 2 Patu, Andræâ-Claudio (André Claude); Le Tort, Bartholomæus (February 1745). Rivard, Franciscus (Dominique-François), ed. Theses Mathematicæ De Mathesi Generatim (in Latin). Collegio Dormano–Bellovaco (Collège de Dormans–Beauvais), Paris: Ph. N. Lottin. p. 6. Retrieved 2017-08-06.
  9. 1 2 Lemonnier, Petro (Pierre) (1750). Genneau, Ludovicum (Ludovico); Rollin, Jacobum (Jacques), eds. Physica generalis. Cursus Philosophicus Ad Scholarum Usum Accomodatus (in Latin). 3. Collegio Harcuriano (Collège d'Harcourt), Paris. pp. 303–. Retrieved 2017-08-06.
  10. 1 2 Thysbaert, Jan-Frans (1774). "Articulus II: De situ lineæ rectæ ad Circularem; & de mensura angulorum, quorum vertex non est in circuli centro. §1. De situ lineæ rectæ ad Circularem. Definitio II: [102]". Geometria elementaria et practica (in Latin). Lovanii, e typographia academica. p. 30, foldout. Retrieved 2017-08-06.
  11. 1 2 van Haecht, Joannes (1784). "Articulus III: De secantibus circuli: Corollarium III: [109]". Geometria elementaria et practica: quam in usum auditorum (in Latin). Lovanii, e typographia academica. p. 24, foldout. Retrieved 2017-08-06.
  12. 1 2 3 Cajori, Florian (1952) [March 1929]. A History of Mathematical Notations. 2 (2 (3rd corrected printing of 1929 issue) ed.). Chicago, USA: Open court publishing company. p. 173. ISBN 978-1-60206-714-1. 1602067147. Retrieved 2015-11-11. (NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.)
  13. 1 2 3 Swanson, Todd; Andersen, Janet; Keeley, Robert (1999). "5 (Trigonometric Functions)". Precalculus: A Study of Functions and Their Applications (PDF). Harcourt Brace & Company. p. 344. Archived (PDF) from the original on 2003-06-17. Retrieved 2015-11-12.
  14. 1 2 3 4 Gottschalk, Walter Helbig (2002). Some Quaint & Curious & Almost Forgotten Trig Functions (PDF). Gottschalk's Gestalts - A Series Illustrating Innovative Forms of the Organization & Exposition of Mathematics. 80. Providence, Rhode Island, USA: Infinite Vistas Press. PVD RI, GG80. Archived (PDF) from the original on 2013-09-25. Retrieved 2015-11-17.
  15. 1 2 3 Frye, Albert I. (1918) [1913]. Civil engineer's pocket-book: a reference-book for engineers, contractors and students containing rules, data, methods, formulas and tables (2 (corrected) ed.). New York, USA; London, UK: D. Van Nostrand Company; Constable and Company, Ltd. Retrieved 2015-11-16.
  16. 1 2 Kenyon, Alfred Monroe; Ingold, Louis (1913). Trigonometry. New York, USA: The Macmillan Company. p. 5. Retrieved 2015-12-08.
  17. 1 2 Hudson, Ralph Gorton; Lipka, Joseph (1917). A Manual of Mathematics. New York, USA: John Wiley & sons. p. 68. Retrieved 2015-12-08.
  18. 1 2 3 4 5 6 Weisstein, Eric W. (2015) [2005]. "Exsecant". MathWorld. Wolfram Research, Inc. Archived from the original on 2005-11-29. Retrieved 2015-11-05.
  19. 1 2 Shaneyfelt, Ted V. "德博士的 Notes About Circles, ज्य, & कोज्य: What in the world is a hacovercosine?". Hilo, Hawaii: University of Hawaii. Archived from the original on 2015-09-19. Retrieved 2015-11-08.
  20. 1 2 3 4 Oldham, Keith B.; Myland, Jan C.; Spanier, Jerome (2009) [1987]. "33.13. The Secant sec(x) and Cosecant csc(x) functions - Cognate functions". An Atlas of Functions: with Equator, the Atlas Function Calculator (2 ed.). Springer Science+Business Media, LLC. p. 336. ISBN 978-0-387-48806-6. LCCN 2008937525. doi:10.1007/978-0-387-48807-3.
  21. 1 2 3 4 Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). "Review Exercises [100] Secondary Trigonometric Functions". Written at Ann Arbor, Michigan, USA. Trigonometry. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. p. 125. Retrieved 2017-08-12.
  22. 1 2 3 Weisstein, Eric W. (2015) [2013]. "Excosecant". MathWorld. Wolfram Research, Inc. Archived from the original on 2014-03-26. Retrieved 2015-11-05.
  23. 1 2 Bohannan, Rosser Daniel (1904) [1903]. "$131. The Versed Sine, Exsecant and Coexsecant. §132. Exercises". Plane Trigonometry. Ohio State University: Allyn and Bacon, Boston, USA / J. S. Cushing & Co. — Berwick & Smith Co., Norwood, MA. pp. 235–236. Retrieved 2017-07-09.
  24. 1 2 3 4 5 6 van Vlijmen, Oscar (2005-12-28) [2003]. "Goniology". Eenheden, constanten en conversies. Archived from the original on 2009-10-28. Retrieved 2015-11-28.
  25. ↑ Galilei, Galileo (1632). Dialogo di Galileo Galilei sopra i due massimi sistemi del mondo Tolemaico e Copernicano [Dialogue on the Two Chief World Systems, Ptolemaic and Copernican] (in Italian).
  26. ↑ Galilei, Galileo (1997-05-25) [1632]. Finocchiaro, Maurice A., ed. Galileo on the World Systems: A New Abridged Translation and Guide. University of California Press. ISBN 9780520918221. ISBN 0520918223. Retrieved 2017-07-30. […] Galileo's word is segante (meaning secant), but he clearly intends exsecant; an exsecant is defined as the part of a secant external to the circle […]
  27. 1 2 Hawking, Stephen William, ed. (2002). On the Shoulders of Giants: The Great Works of Physics and Astronomy. Philadelphia, USA: Running Press. ISBN 0-7624-1698-X. LCCN 2002100441. Retrieved 2017-07-31.
  28. 1 2 3 Stávek, Jiří (2017-03-10) [2017-02-26]. "On the Hidden Beauty of Trigonometric Functions". Applied Physics Research. Prague, CZ: Canadian Center of Science and Education. 9 (2): 57–64. ISSN 1916-9639. doi:10.5539/apr.v9n2p57. ISSN 1916-9647. Archived from the original on 2017-07-31. Retrieved 2017-07-31.
  29. 1 2 Simpson, David G. (2001-11-08). "AUXTRIG" (Fortran 90 source code). Greenbelt, Maryland, USA: NASA Goddard Space Flight Center. Archived from the original on 2008-06-16. Retrieved 2015-10-26.
  30. 1 2 van den Doel, Kees (2010-01-25). "jass.utils Class Fmath". JASS - Java Audio Synthesis System. 1.25. Archived from the original on 2007-09-02. Retrieved 2015-10-26.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.