Johnson solid

In geometry, a Johnson solid is a strictly convex polyhedron, which is not uniform (i.e., not a Platonic solid, Archimedean solid, prism or antiprism), and each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J₁); it has 1 square face and 4 triangular faces.

As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid (J₂) is an example that actually has a degree-5 vertex.

Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the faces of Johnson solids always have 3, 4, 5, 6, 8, or 10 sides.

In 1966, Norman Johnson published a list which included all 92 solids, and gave them their names and numbers. He did not prove that there were only 92, but he did conjecture that there were no others. Victor Zalgaller in 1969 proved that Johnson's list was complete.

Of the Johnson solids, the elongated square gyrobicupola (J₃₇), also called the pseudorhombicuboctahedron,^[1] is unique in being locally vertex-uniform: there are 4 faces at each vertex, and their arrangement is always the same: 3 squares and 1 triangle. However, it is not vertex-transitive, as it has different isometry at different vertices, making it a Johnson solid rather than an Archimedean solid.

Names

The naming of Johnson solids follows a flexible and precise descriptive formula, such that many solids can be named in different ways without compromising their accuracy as a description. Most Johnson solids can be constructed from the first few (pyramids, cupolae, and rotunda), together with the Platonic and Archimedean solids, prisms, and antiprisms; the centre of a particular solid's name will reflect these ingredients. From there, a series of prefixes are attached to the word to indicate additions, rotations and transformations:

• Bi- indicates that two copies of the solid in question are joined base-to-base. For cupolae and rotundae, the solids can be joined so that either like faces (ortho-) or unlike faces (gyro-) meet. Using this nomenclature, an octahedron can be described as a square bipyramid, a cuboctahedron as a triangular gyrobicupola, and an icosidodecahedron as a pentagonal gyrobirotunda.
• Elongated indicates a prism is joined to the base of the solid in question, or between the bases in the case of Bi- solids. A rhombicuboctahedron can thus be described as an elongated square orthobicupola.
• Gyroelongated indicates an antiprism is joined to the base of the solid in question or between the bases in the case of Bi- solids. An icosahedron can thus be described as a gyroelongated pentagonal bipyramid.
• Augmented indicates another polyhedron, namely a pyramid or cupola, is joined to one or more faces of the solid in question.
• Diminished indicates a pyramid or cupola is removed from one or more faces of the solid in question.
• Gyrate indicates a cupola mounted on or featured in the solid in question is rotated such that different edges match up, as in the difference between ortho- and gyrobicupolae.

The last three operations — augmentation, diminution, and gyration — can be performed multiple times certain large solids. Bi- & Tri- indicate a double and treble operation respectively. For example, a bigyrate solid has two rotated cupolae, and a tridiminished solid has three removed pyramids or cupolae.

In certain large solids, a distinction is made between solids where altered faces are parallel and solids where altered faces are oblique. Para- indicates the former, that the solid in question has altered parallel faces, and Meta- the latter, altered oblique faces. For example, a parabiaugmented solid has had two parallel faces augmented, and a metabigyrate solid has had 2 oblique faces gyrated.

The last few Johnson solids have names based on certain polygon complexes from which they are assembled. These names are defined by Johnson^[2] with the following nomenclature:

• A lune is a complex of two triangles attached to opposite sides of a square.
• Spheno- indicates a wedgelike complex formed by two adjacent lunes. Dispheno- indicates two such complexes.
• Hebespheno- indicates a blunt complex of two lunes separated by a third lune.
• Corona is a crownlike complex of eight triangles.
• Megacorona is a larger crownlike complex of 12 triangles.
• The suffix -cingulum indicates a belt of 12 triangles.

Enumeration

Pyramids

The first two Johnson solids, J1 and J2, are pyramids. The triangular pyramid is the regular tetrahedron, so it is not a Johnson solid.

Pyramids

Regular	J1	J2
Triangular pyramid (Tetrahedron)	Square pyramid	Pentagonal pyramid

Cupolae and rotunda

The next four Johnson solids are three cupolae and one rotunda. They represent sections of uniform polyhedra.

Cupola				Rotunda
Uniform	J3	J4	J5	J6
Triangular prism	Triangular cupola	Square cupola	Pentagonal cupola	Pentagonal rotunda
Related uniform polyhedra
	Cuboctahedron	Rhombicuboctahedron	Rhombicosidodecahedron	Icosidodecahedron

Elongated and gyroelongated pyramids

The next five Johnson solids are elongated and gyroelongated pyramids. These represent the composite or augmentation of two polyhedra. In the gyroelongated triangular pyramid, three pairs of adjacent triangles are coplanar and form non-square rhombi, so it is not a Johnson solid.

Elongated pyramids (or augmented prisms)			Gyroelongated pyramids (or augmented antiprisms)
J7	J8	J9	Coplanar	J10	J11
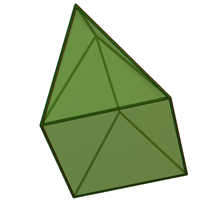
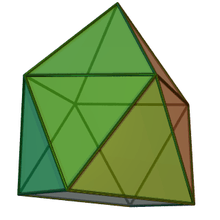
Elongated triangular pyramid	Elongated square pyramid	Elongated pentagonal pyramid	Gyroelongated triangular pyramid	Gyroelongated square pyramid	Gyroelongated pentagonal pyramid
Augmented triangular prism	Augmented cube	Augmented pentagonal prism	Augmented octahedron	Augmented square antiprism	Augmented pentagonal antiprism
Augmented from polyhedra
tetrahedron triangular prism	square pyramid cube	pentagonal pyramid pentagonal prism	tetrahedron octahedron	square pyramid square antiprism	pentagonal pyramid pentagonal antiprism

Bipyramids

The next six Johnson solids are bipyramids, elongated bipyramids, and gyroelongated bipyramids:

Bipyramids			Elongated bipyramids			Gyroelongated bipyramids
J12	Regular	J13	J14	J15	J16	Coplanar	J17	Regular
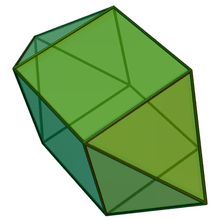
Triangular bipyramid	Square bipyramid (octahedron)	Pentagonal bipyramid	Elongated triangular bipyramid	Elongated square bipyramid	Elongated pentagonal bipyramid	Gyroelongated triangular bipyramid (rhombohedron)	Gyroelongated square bipyramid	Gyroelongated pentagonal bipyramid (icosahedron)
Augmented from polyhedra
tetrahedron	square pyramid	pentagonal pyramid	tetrahedron triangular prism	square pyramid cube	pentagonal pyramid pentagonal prism	tetrahedron Octahedron	square pyramid square antiprism	pentagonal pyramid pentagonal antiprism

Elongated cupolae and rotundae

Elongated cupola					Elongated rotunda	Gyroelongated cupola					Gyroelongated rotunda
Coplanar	J18	J19	J20	Coplanar	J21	Concave	J22	J23	J24	Coplanar	J25
Elongated digonal cupola	Elongated triangular cupola	Elongated square cupola	Elongated pentagonal cupola	Elongated hexagonal cupola	Elongated pentagonal rotunda	Gyroelongated digonal cupola	Gyroelongated triangular cupola	Gyroelongated square cupola	Gyroelongated pentagonal cupola	Gyroelongated hexagonal cupola	Gyroelongated pentagonal rotunda
Augmented from polyhedra
Square prism Triangular prism	Hexagonal prism Triangular cupola	Octagonal prism Square cupola	Decagonal prism Pentagonal cupola	Dodecagonal prism Hexagonal cupola	Decagonal prism Pentagonal rotunda	square antiprism Triangular prism	Hexagonal antiprism Triangular cupola	Octagonal antiprism Square cupola	Decagonal antiprism Pentagonal cupola		Decagonal antiprism Pentagonal rotunda

Bicupolae

The triangular gyrobicupola is a semiregular polyhedron (in this case an Archimedean solid), so it is not a Johnson solid.

Orthobicupola					Gyrobicupola
Coplanar	J27	J28	J30	Coplanar	J26	Semiregular	J29	J31	Coplanar
Digonal orthobicupola	Triangular orthobicupola	Square orthobicupola	Pentagonal orthobicupola	Hexagonal orthobicupola	Digonal gyrobicupola gyrobifastigium	Triangular gyrobicupola (cuboctahedron)	Square gyrobicupola	Pentagonal gyrobicupola	Hexagonal gyrobicupola
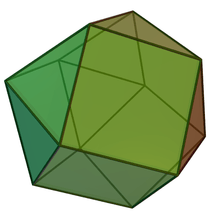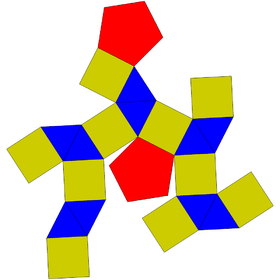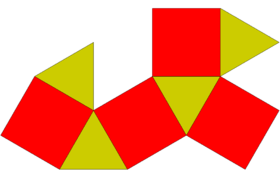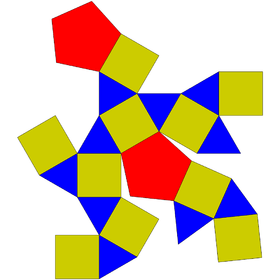Augmented from polyhedron

Bianticupolae

All of the orthobianticupola have coplanar faces. The gyrobianticupola are another construction for the snub antiprisms.

Orthobianticupola					Gyrobianticupola
Flat	Coplanar	Coplanar	Coplanar	Flat	J84	Regular	J85	Concave	Flat
Digonal orthobianticupola	Triangular orthobianticupola	Square orthobianticupola	Pentagonal orthobianticupola	Hexagonal orthobianticupola	Diagonal gyrobianticupola	Triangular gyrobianticupola Icosahedron	Square gyrobianticupola	Pentagonal orthobianticupola	Hexagonal orthobianticupola

Cupola-rotundae and birotunda

Cupola-rotunda		Birotunda
J32	J33	J34	Semiregular
Pentagonal orthocupolarotunda	Pentagonal gyrocupolarotunda	Pentagonal orthobirotunda	Pentagonal gyrobirotunda icosidodecahedron
Augumented from polyhedra
Pentagonal cupola Pentagonal rotunda		Pentagonal rotunda

Elongated bicupolae

Elongated orthobicupola				Elongated gyrobicupola
Coplanar	J35	Semiregular	J38	Coplanar	J36	J37	J39
Elongated digonal orthobicupola	Elongated triangular orthobicupola	Elongated square orthobicupola (rhombicuboctahedron)	Elongated pentagonal orthobicupola	Elongated digonal gyrobicupola	Elongated triangular gyrobicupola	Elongated square gyrobicupola	Elongated pentagonal gyrobicupola

Elongated cupola-rotundae and birotundae

Elongated cupolarotunda		Elongated birotunda
J40	J41	J42	J43
Elongated pentagonal orthocupolarotunda	Elongated pentagonal gyrocupolarotunda	Elongated pentagonal orthobirotunda	Elongated pentagonal gyrobirotunda

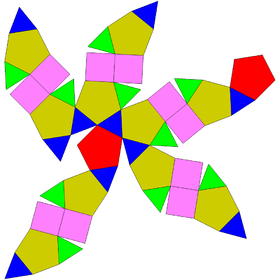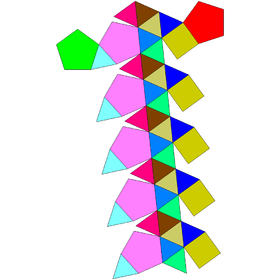
Gyroelongated bicupolae, cupola-rotunda, and birotunda

These Johnson solids have 2 chiral forms.

Gyroelongated bicupola				Gyroelongated cupolarotunda	Gyroelongated birotunda
Concave	J44	J45	J46	J47	J48
Gyroelongated digonal bicupola	Gyroelongated triangular bicupola	Gyroelongated square bicupola	Gyroelongated pentagonal bicupola	Gyroelongated pentagonal cupolarotunda	Gyroelongated pentagonal birotunda
Augmented from polyhedra
Triangular prism Square antiprism	Triangular cupola Hexagonal antiprism	Square cupola Octagonal antiprism	Pentagonal cupola Decagonal antiprism	Pentagonal cupola Pentagonal rotunda Decagonal antiprism	Pentagonal rotunda Decagonal antiprism

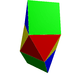
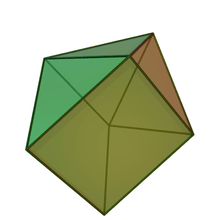
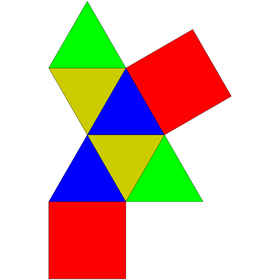
Augmented triangular prisms

J7 (repeat)	J49	J50	J51
Elongated triangular pyramid	Augmented triangular prism	Biaugmented triangular prism	Triaugmented triangular prism
Augumented from polyhedra
Triangular prism tetrahedron	Triangular prism Square pyramid

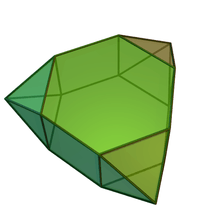
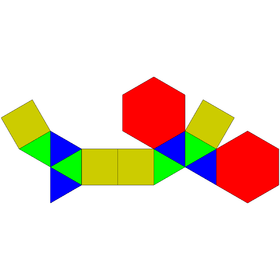
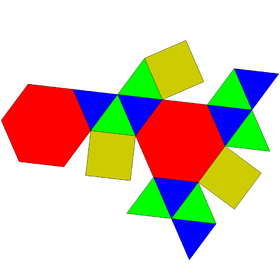
Augmented pentagonal and hexagonal prisms

Augmented pentagonal prisms		Augmented hexagonal prisms
J52	J53	J54	J55	J56	J57
Augmented pentagonal prism	Biaugmented pentagonal prism	Augmented hexagonal prism	Parabiaugmented hexagonal prism	Metabiaugmented hexagonal prism	Triaugmented hexagonal prism
Augumented from polyhedra
Pentagonal prism Square pyramid		Hexagonal prism Square pyramid

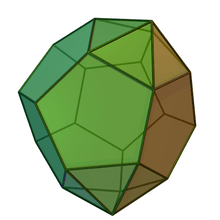
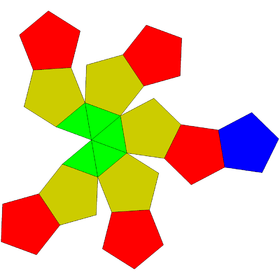
Augmented dodecahedra

Regular	J58	J59	J60	J61
Dodecahedron	Augmented dodecahedron	Parabiaugmented dodecahedron	Metabiaugmented dodecahedron	Triaugmented dodecahedron
Augumented from polyhedra
Dodecahedron and pentagonal pyramid

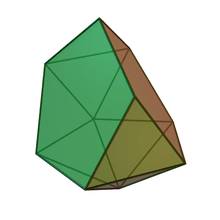
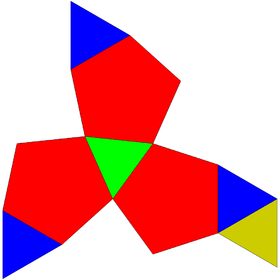
Diminished icosahedra

J63	J62	J11 (Repeated)	Regular	J64
Tridiminished icosahedron	Metabidiminished icosahedron	Diminished icosahedron (Gyroelongated pentagonal pyramid)	Icosahedron	Augmented tridiminished icosahedron
Augumented from polyhedra
Tridiminished icosahedron, pentagonal pyramid and tetrahedron

Augmented truncated tetrahedron and truncated cubes

J65	J66	J67
Augmented truncated tetrahedron	Augmented truncated cube	Biaugmented truncated cube
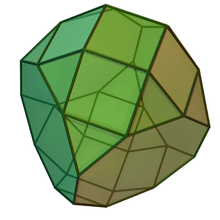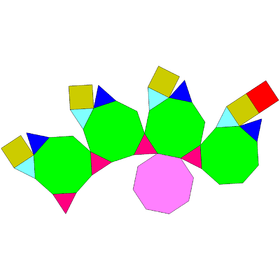Augumented from polyhedra
truncated tetrahedron triangular cupola	truncated cube square cupola

Augmented truncated dodecahedra

Semiregular	J68	J69	J70	J71
Truncated dodecahedron	Augmented truncated dodecahedron	Parabiaugmented truncated dodecahedron	Metabiaugmented truncated dodecahedron	Triaugmented truncated dodecahedron

Gyrate rhombicosidodecahedra

J72	J73	J74	J75
Gyrate rhombicosidodecahedron	Parabigyrate rhombicosidodecahedron	Metabigyrate rhombicosidodecahedron	Trigyrate rhombicosidodecahedron

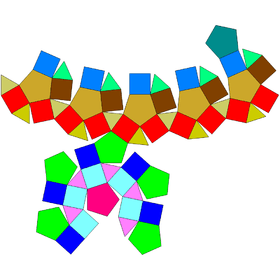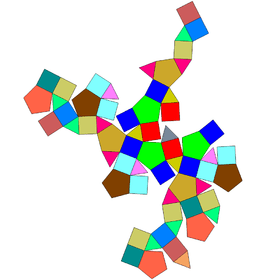Diminished rhombicosidodecahedra

J76	J77	J78	J79
Diminished rhombicosidodecahedron	Paragyrate diminished rhombicosidodecahedron	Metagyrate diminished rhombicosidodecahedron	Bigyrate diminished rhombicosidodecahedron
J80	J81	J82	J83
Parabidiminished rhombicosidodecahedron	Metabidiminished rhombicosidodecahedron	Gyrate bidiminished rhombicosidodecahedron	Tridiminished rhombicosidodecahedron

Snub antiprisms

The snub antiprisms can be constructed as an alternation of a truncated antiprism. Two are Johnson solids, one is a regular, and the rest can not be constructed with regular triangles.

J84	Regular	J85	Concave
Snub disphenoid ss{2,4}	Icosahedron ss{2,6}	Snub square antiprism ss{2,8}	Snub pentagonal antiprism ss{2,10}...

Others

J86	J87	J88
Sphenocorona	Augmented sphenocorona	Sphenomegacorona
J89	J90	J91	J92
Hebesphenomegacorona	Disphenocingulum	Bilunabirotunda	Triangular hebesphenorotunda

Classification by types of faces

Triangle-faced Johnson solids

Five Johnson solids are deltahedra, with all equilateral triangle faces:

J12 Triangular bipyramid J13 Pentagonal bipyramid J17 Gyroelongated square bipyramid

J51 Triaugmented triangular prism J84 Snub disphenoid

Triangle and square-faced Johnson solids

Twenty four Johnson solids have only triangle or square faces:

J1 Square pyramid J7 Elongated triangular pyramid J8 Elongated square pyramid J10 Gyroelongated square pyramid J14 Elongated triangular bipyramid J15 Elongated square bipyramid J16 Elongated pentagonal bipyramid J26 Gyrobifastigium

J27 Triangular orthobicupola J28 Square orthobicupola J29 Square gyrobicupola J35 Elongated triangular orthobicupola J36 Elongated triangular gyrobicupola J37 Elongated square gyrobicupola J44 Gyroelongated triangular bicupola J45 Gyroelongated square bicupola

J49 Augmented triangular prism J50 Biaugmented triangular prism J85 Snub square antiprism J86 Sphenocorona J87 Augmented sphenocorona J88 Sphenomegacorona J89 Hebesphenomegacorona J90 Disphenocingulum

Triangle and pentagonal-faced Johnson solids

Eleven Johnson solids have only triangle and pentagonal faces:

J2 Pentagonal pyramid J11 Gyroelongated pentagonal pyramid J34 Pentagonal orthobirotunda J48 Gyroelongated pentagonal birotunda J58 Augmented dodecahedron J59 Parabiaugmented dodecahedron

J60 Metabiaugmented dodecahedron J61 Triaugmented dodecahedron J62 Metabidiminished icosahedron J63 Tridiminished icosahedron J64 Augmented tridiminished icosahedron

Triangle, square and hexagonal-faced Johnson solids

Eight Johnson solids have only triangle, square and hexagonal faces:

J3 Triangular cupola J18 Elongated triangular cupola J22 Gyroelongated triangular cupola J54 Augmented hexagonal prism

J55 Parabiaugmented hexagonal prism J56 Metabiaugmented hexagonal prism J57 Triaugmented hexagonal prism J65 Augmented truncated tetrahedron

Triangle, square and octagonal-faced Johnson solids

Five Johnson solids have only triangle, square and octagonal faces:

J4 Square cupola J19 Elongated square cupola J23 Gyroelongated square cupola

J66 Augmented truncated cube J67 Biaugmented truncated cube

Circumscribable Johnson solids

25 of the Johnson solids have vertices that exist on the surface of a sphere: 1-6,11,19,27,34,37,62,63,72-83. All of them can be seen to be related to a regular or uniform polyhedron by gyration, diminishment, or dissection.^[3]

Octahedron	Cuboctahedron		Rhombicuboctahedron
J1	J3	J27	J4	J19	J37

Icosahedron				Icosidodecahedron
J2	J63	J62	J11	J6	J34

Rhombicosidodecahedron (diminished)

J5

J76

J80

J81

J83

Rhombicosidodecahedron (+gyration)

J72

J73

J74

J75

J77

J78

J79

J82

See also

• Near-miss Johnson solid
• Catalan solid
• Toroidal polyhedron

References

• Johnson, Norman W. (1966). "Convex Solids with Regular Faces". Canadian Journal of Mathematics. 18: 169–200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8.  Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• Zalgaller, Victor A. (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. Zbl 0177.24802. No ISBN.  The first proof that there are only 92 Johnson solids: see also Zalgaller, Victor A. (1967). "Convex Polyhedra with Regular Faces". Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova (in Russian). 2: 1–221. ISSN 0373-2703. Zbl 0165.56302. 
• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.  Chapter 3 Further Convex polyhedra

External links

• Sylvain Gagnon, "Convex polyhedra with regular faces", Structural Topology, No. 6, 1982, 83-95.
• Paper Models of Polyhedra Many links
• Johnson Solids by George W. Hart.
• Images of all 92 solids, categorized, on one page
• Weisstein, Eric W. "Johnson Solid". MathWorld. 

• VRML models of Johnson Solids by Jim McNeill
• VRML models of Johnson Solids by Vladimir Bulatov
• CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4-dimensional space