Domino computer
A domino computer is a mechanical computer built using dominoes[1] to represent mechanical amplification or logic gating of digital signals. Because of the existence of multiple schemes, domino computer will be used in this article to denote any particular scheme that uses the mentioned base phenomenon (of domino sequences) for building machines equivalent to a computer. This choice of terminology may be somewhat arbitrary, because only few resources write on this topic.[2]
Basic phenomenon
Sequences of standing dominoes (so that each topples the next one) can be arranged to demonstrate digital concepts such as amplification and digital signals. It is some digital information that is conducted by a string of dominoes, thus this effect differs from phenomena where:
- energy is conducted without amplification, thus dissipating; or
- amplification is applied to non-digital signals, allowing noise effects to occur.
The Domino Day event shows many constructs, mainly with purpose of entertainment. Some constructs may remind people of digital circuits. Some of them suggest that not only telegraph-like tools can be shown, but also simple information processing modules can be built.
It is possible to use this phenomenon for constructing unconventional computing tools.[1][2][3] The base phenomenon is sufficient to achieve this goal,[2] but also sophisticated “mechanical synapses” can be used (see online [4]), to the analogy of electrical synapses or chemical synapses.
Logical aspects
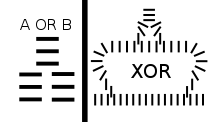
The logic gate OR is very natural in dominoes. The problem is which gate we should add to OR, and obtain a functionally complete set. Note that no domino gate can produce output 1 with all inputs 0, so we cannot make NOT, therefore we cannot even make IMPLIES without an external 'power source' sequence. Once we admit it, NOT is realized and we have a complete set.
But it is however distant to lead in a sequence from one source to many gates in each suitable timing. Let us suppose we do not have one.
A root breaking system is basically needed if one wants a logical connective with output 0 for input 1. Let P$Q be the gate in which the sequence to be turned down by P is broken by that by Q. Then P$Q is logically equivalent to P AND (NOT Q), if the input Q is earlier than P. The set of OR and $ can represent any logical connectives in any arity except for ones which generates 1 with all inputs 0.
Similarly, XOR can be realized with the gate in a diagram above as a bi-root breaking system.
The problems of these two root breaking systems is that they heavily depend on the simultaneity of two inputs. In the gate of XOR one input may destroy the opposite input root tracking back. Note that the expression of P AND Q, P$(P$Q) OR Q$(Q$P) is symmetric, hence does not depend on the simultaneity, and with no worry of tracking back, though it is complicated.
Record
The current record for domino computers is a 4 bit adder.
At the Manchester Science Festival in 2012, mathematician Matt Parker and a team of volunteers worked together to build a domino binary adder which could add two three-bit inputs and produce a 4-bit output, which ran successfully. The following day, they attempted to build a 5-bit adder, which they completed, but the final test run had some errors (one due to signal bleed between chains of dominoes, and one timing issue).[5]
See also
- Domino logic
- The concept is mentioned in the book I Am a Strange Loop
Notes
- 1 2 Domino computer
- 1 2 3 Domino computers Archived August 16, 2006, at the Wayback Machine., a detailed description written by David Johnston
- ↑ James Maguire: IBM Creates Molecular Computer Circuit Archived July 19, 2006, at the Wayback Machine. NewsFactor Magazine Online, 2006. A topic in the intersection of molecular computing and domino computer
- ↑ Perrucci, Mike: Domino Toppling.
- ↑ https://www.youtube.com/watch?v=OpLU__bhu2w
External links
- Kybernetikos, (kyb). "Domino Computation".