Convolutional code
In telecommunication, a convolutional code is a type of error-correcting code that generates parity symbols via the sliding application of a boolean polynomial function to a data stream. The sliding application represents the 'convolution' of the encoder over the data, which gives rise to the term 'convolutional coding.' The sliding nature of the convolutional codes facilitates trellis decoding using a time-invariant trellis. Time invariant trellis decoding allows convolutional codes to be maximum-likelihood soft-decision decoded with reasonable complexity.
The ability to perform economical maximum likelihood soft decision decoding is one of the major benefits of convolutional codes. This is in contrast to classic block codes, which are generally represented by a time-variant trellis and therefore are typically hard-decision decoded. Convolutional codes are often characterized by the base code rate and the depth (or memory) of the encoder [n,k,K]. The base code rate is typically given as n/k, where n is the input data rate and k is the output symbol rate. The depth is often called the "constraint length" 'K', where the output is a function of the current input as well as the previous K-1 inputs. The depth may also be given as the number of memory elements 'v' in the polynomial or the maximum possible number of states of the encoder (typically 2^v).
Convolutional codes are often described as continuous. However, it may also be said that convolutional codes have arbitrary block length, rather than being continuous, since most real-world convolutional encoding is performed on blocks of data. Convolutionally encoded block codes typically employ termination. The arbitrary block length of convolutional codes can also be contrasted to classic block codes, which generally have fixed block lengths that are determined by algebraic properties.
The code rate of a convolutional code is commonly modified via symbol puncturing. For example, a convolutional code with a 'mother' code rate n/k=1/2 may be punctured to a higher rate of, for example, 7/8 simply by not transmitting a portion of code symbols. The performance of a punctured convolutional code generally scales well with the amount of parity transmitted. The ability to perform economical soft decision decoding on convolutional codes, as well as the block length and code rate flexibility of convolutional codes, makes them very popular for digital communications.
History
Convolutional codes were introduced in 1955 by Peter Elias. It was thought that convolutional codes could be decoded with arbitrary quality at the expense of computation and delay. In 1967 Andrew Viterbi determined that convolutional codes could be maximum-likelihood decoded with reasonable complexity using time invariant trellis based decoders — the Viterbi algorithm. Other trellis-based decoder algorithms were later developed, including the BCJR decoding algorithm.
Recursive systematic convolutional codes were invented by Claude Berrou around 1991. These codes proved especially useful for iterative processing including the processing of concatenated codes such as turbo codes.
Using the "convolutional" terminology, a classic convolutional code might be considered a Finite impulse response (FIR) filter, while a recursive convolutional code might be considered an Infinite impulse response (IIR) filter.
Where convolutional codes are used
Convolutional codes are used extensively to achieve reliable data transfer in numerous applications, such as digital video, radio, mobile communications and satellite communications. These codes are often implemented in concatenation with a hard-decision code, particularly Reed Solomon. Prior to turbo codes such constructions were the most efficient, coming closest to the Shannon limit.
Convolutional encoding
To convolutionally encode data, start with k memory registers, each holding 1 input bit. Unless otherwise specified, all memory registers start with a value of 0. The encoder has n modulo-2 adders (a modulo 2 adder can be implemented with a single Boolean XOR gate, where the logic is: 0+0 = 0, 0+1 = 1, 1+0 = 1, 1+1 = 0), and n generator polynomials — one for each adder (see figure below). An input bit m1 is fed into the leftmost register. Using the generator polynomials and the existing values in the remaining registers, the encoder outputs n symbols. These symbols may be transmitted or punctured depending on the desired code rate. Now bit shift all register values to the right (m1 moves to m0, m0 moves to m−1) and wait for the next input bit. If there are no remaining input bits, the encoder continues shifting until all registers have returned to the zero state (flush bit termination).
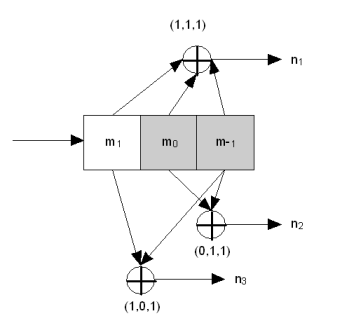
The figure below is a rate 1⁄3 ( m⁄n) encoder with constraint length (k) of 3. Generator polynomials are G1 = (1,1,1), G2 = (0,1,1), and G3 = (1,0,1). Therefore, output bits are calculated (modulo 2) as follows:
- n1 = m1 + m0 + m−1
- n2 = m0 + m−1
- n3 = m1 + m−1.
Recursive and non-recursive codes
The encoder on the picture above is a non-recursive encoder. Here's an example of a recursive one and as such it admits a feedback structure:

The example encoder is systematic because the input data is also used in the output symbols (Output 2). Codes with output symbols that do not include the input data are called non-systematic.
Recursive codes are typically systematic and, conversely, non-recursive codes are typically non-systematic. It isn't a strict requirement, but a common practice.
The example encoder in Img. 2. is an 8-state encoder because the 3 registers will create 8 possible encoder states (23). A corresponding decoder trellis will typically use 8 states as well.
Recursive systematic convolutional (RSC) codes have become more popular due to their use in Turbo Codes. Recursive systematic codes are also referred to as pseudo-systematic codes.
Other RSC codes and example applications include:

Useful for LDPC code implementation and as inner constituent code for serial concatenated convolutional codes (SCCC's).

Useful for SCCC's and multidimensional turbo codes.
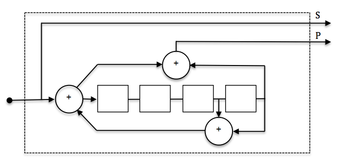
Useful as constituent code in low error rate turbo codes for applications such as satellite links. Also suitable as SCCC outer code.
Impulse response, transfer function, and constraint length
A convolutional encoder is called so because it performs a convolution of the input stream with the encoder's impulse responses:
where x is an input sequence, yj is a sequence from output j and hj is an impulse response for output j.
A convolutional encoder is a discrete linear time-invariant system. Every output of an encoder can be described by its own transfer function, which is closely related to the generator polynomial. An impulse response is connected with a transfer function through Z-transform.
Transfer functions for the first (non-recursive) encoder are:
Transfer functions for the second (recursive) encoder are:
Define m by
where, for any rational function ,
- .
Then m is the maximum of the polynomial degrees of the , and the constraint length is defined as . For instance, in the first example the constraint length is 3, and in the second the constraint length is 4.
Trellis diagram
A convolutional encoder is a finite state machine. An encoder with n binary cells will have 2n states.
Imagine that the encoder (shown on Img.1, above) has '1' in the left memory cell (m0), and '0' in the right one (m−1). (m1 is not really a memory cell because it represents a current value). We will designate such a state as "10". According to an input bit the encoder at the next turn can convert either to the "01" state or the "11" state. One can see that not all transitions are possible for (e.g., a decoder can't convert from "10" state to "00" or even stay in "10" state).
All possible transitions can be shown as below:

An actual encoded sequence can be represented as a path on this graph. One valid path is shown in red as an example.
This diagram gives us an idea about decoding: if a received sequence doesn't fit this graph, then it was received with errors, and we must choose the nearest correct (fitting the graph) sequence. The real decoding algorithms exploit this idea.
Free distance and error distribution
The free distance (d) is the minimal Hamming distance between different encoded sequences. The correcting capability (t) of a convolutional code is the number of errors that can be corrected by the code. It can be calculated as
Since a convolutional code doesn't use blocks, processing instead a continuous bitstream, the value of t applies to a quantity of errors located relatively near to each other. That is, multiple groups of t errors can usually be fixed when they are relatively far apart.
Free distance can be interpreted as the minimal length of an erroneous "burst" at the output of a convolutional decoder. The fact that errors appear as "bursts" should be accounted for when designing a concatenated code with an inner convolutional code. The popular solution for this problem is to interleave data before convolutional encoding, so that the outer block (usually Reed-Solomon) code can correct most of the errors.
Decoding convolutional codes
Several algorithms exist for decoding convolutional codes. For relatively small values of k, the Viterbi algorithm is universally used as it provides maximum likelihood performance and is highly parallelizable. Viterbi decoders are thus easy to implement in VLSI hardware and in software on CPUs with SIMD instruction sets.
Longer constraint length codes are more practically decoded with any of several sequential decoding algorithms, of which the Fano algorithm is the best known. Unlike Viterbi decoding, sequential decoding is not maximum likelihood but its complexity increases only slightly with constraint length, allowing the use of strong, long-constraint-length codes. Such codes were used in the Pioneer program of the early 1970s to Jupiter and Saturn, but gave way to shorter, Viterbi-decoded codes, usually concatenated with large Reed-Solomon error correction codes that steepen the overall bit-error-rate curve and produce extremely low residual undetected error rates.
Both Viterbi and sequential decoding algorithms return hard decisions: the bits that form the most likely codeword. An approximate confidence measure can be added to each bit by use of the Soft output Viterbi algorithm. Maximum a posteriori (MAP) soft decisions for each bit can be obtained by use of the BCJR algorithm.
Popular convolutional codes
An especially popular Viterbi-decoded convolutional code, used at least since the Voyager program has a constraint length k of 7 and a rate r of 1/2.
- Longer constraint lengths produce more powerful codes, but the complexity of the Viterbi algorithm increases exponentially with constraint lengths, limiting these more powerful codes to deep space missions where the extra performance is easily worth the increased decoder complexity.
- Mars Pathfinder, Mars Exploration Rover and the Cassini probe to Saturn use a k of 15 and a rate of 1/6; this code performs about 2 dB better than the simpler k=7 code at a cost of 256× in decoding complexity (compared to Voyager mission codes).
Punctured convolutional codes
Puncturing is a technique used to make a m/n rate code from a "basic" low-rate (e.g., 1/n) code. It is reached by deletion of some bits in the encoder output. Bits are deleted according to a puncturing matrix. The following puncturing matrices are the most frequently used:
| Code rate | Puncturing matrix | Free distance (for NASA standard K=7 convolutional code) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/2 (No perf.) |
|
10 | ||||||||||||||
| 2/3 |
|
6 | ||||||||||||||
| 3/4 |
|
5 | ||||||||||||||
| 5/6 |
|
4 | ||||||||||||||
| 7/8 |
|
3 |
For example, if we want to make a code with rate 2/3 using the appropriate matrix from the above table, we should take a basic encoder output and transmit every first bit from the first branch and every bit from the second one. The specific order of transmission is defined by the respective communication standard.
Punctured convolutional codes are widely used in the satellite communications, for example, in INTELSAT systems and Digital Video Broadcasting.
Punctured convolutional codes are also called "perforated".
Turbo codes: replacing convolutional codes
Simple Viterbi-decoded convolutional codes are now giving way to turbo codes, a new class of iterated short convolutional codes that closely approach the theoretical limits imposed by Shannon's theorem with much less decoding complexity than the Viterbi algorithm on the long convolutional codes that would be required for the same performance. Concatenation with an outer algebraic code (e.g., Reed-Solomon) addresses the issue of error floors inherent to turbo code designs.
See also
References
 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
External links
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, discusses convolutional codes in Chapter 48.
- The Error Correcting Codes (ECC) Page
- Matlab explanations