Convex combination

Given three points

x_{1},x_{2},x_{3}

in a plane as shown in the figure, the point

P

is a convex combination of the three points, while

Q

is not.
(

Q

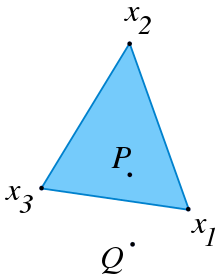
is however an affine combination of the three points, as their affine hull is the entire plane.)

In convex geometry, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1.

More formally, given a finite number of points $x_{1},x_{2},\dots ,x_{n}$ in a real vector space, a convex combination of these points is a point of the form

\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}

where the real numbers $\alpha _{i}$ satisfy $\alpha _{i}\geq 0$ and $\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=1.$

As a particular example, every convex combination of two points lies on the line segment between the points.

The convex hull of the given points is identical to the set of all their convex combinations.

There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval $[0,1]$ is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributions, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).

Other objects

Similarly, a convex combination $X$ of probability distributions $Y_{i}$ is a weighted sum (where $\alpha _{i}$ satisfy the same constraints as above) of its component probability distributions, often called a finite mixture distribution, with probability density function:

f_{{X}}(x)=\sum _{{i=1}}^{{n}}\alpha _{i}f_{{Y_{i}}}(x)

Related constructions

A conical combination is a linear combination with nonnegative coefficients. When a point $x$ is to be used as the reference origin for defining displacement vectors, then $x$ is a convex combination of $n$ points $x_{1},x_{2},\dots ,x_{n}$ if and only if the zero displacement is a non-trivial conical combination of their $n$ respective displacement vectors relative to $x$ .
Weighted means are functionally the same as convex combinations, but they use a different notation. The coefficients (weights) in a weighted mean are not required to sum to 1; instead the sum is explicitly divided from the linear combination.
Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any field.

Convex combination

Other objects

Related constructions

See also