Color charge

Standard Model of particle physics
Fundamental particles of the standard model
Background Particle physics Standard Model Quantum field theory Gauge theory Spontaneous symmetry breaking Higgs mechanism
Constituents Electroweak interaction Quantum chromodynamics CKM matrix Standard Model mathematics
Limitations Strong CP problem Hierarchy problem Neutrino oscillations Physics beyond the Standard Model
Scientists Rutherford · Thomson · Chadwick · Bose · Sudarshan · Koshiba · Davis Jr. · Anderson · Fermi · Dirac · Feynman · Rubbia · Gell-Mann · Kendall · Taylor · Friedman · Powell · P. W. Anderson · Glashow · Iliopoulos · Maiani · Meer · Cowan · Nambu · Chamberlain · Cabibbo · Schwartz · Perl · Majorana · Weinberg · Lee · Ward · Salam · Kobayashi · Maskawa · Yang · Yukawa · 't Hooft · Veltman · Gross · Politzer · Wilczek · Cronin · Fitch · Vleck · Higgs · Englert · Brout · Hagen · Guralnik · Kibble · Ting · Richter

Color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics (QCD).

The "color charge" of quarks and gluons is completely unrelated to the everyday meaning of color.^[1] The term color and the labels red, green, blue became popular simply because of the loose analogy to the primary colors. (Richard Feynman referred to his colleagues as "idiot physicists" for choosing the confusing name.)

Particles have corresponding antiparticles. A particle with red, green, or blue charge has a corresponding antiparticle in which the color charge must be the anticolor of red, green, and blue, respectively, for the color charge to be conserved in particle-antiparticle creation and annihilation. Particle physicists call these antired, antigreen, and antiblue. All three colors mixed together, or any one of these colors and its complement (or negative), is "colorless" or "white" and has a net color charge of zero. Free particles have a color charge of zero: baryons are composed of three quarks, but the individual quarks can have red, green, or blue charges, or negatives; mesons are made from a quark and antiquark, the quark can be any color, and the antiquark will have the negative of that color. This color charge differs from electromagnetic charges since electromagnetic charges have only one kind of value. Positive and negative electrical charges are the same kind of charge as they only differ by the sign.

Shortly after the existence of quarks was first proposed in 1964, Oscar W. Greenberg introduced the notion of color charge to explain how quarks could coexist inside some hadrons in otherwise identical quantum states without violating the Pauli exclusion principle. The theory of quantum chromodynamics has been under development since the 1970s and constitutes an important component of the Standard Model of particle physics.

Red, green, and blue

In quantum chromodynamics, a quark's color can take one of three values or charges, red, green, and blue. An antiquark can take one of three anticolors, called antired, antigreen, and antiblue (represented as cyan, magenta and yellow, respectively). Gluons are mixtures of two colors, such as red and antigreen, which constitutes their color charge. QCD considers eight gluons of the possible nine color–anticolor combinations to be unique; see eight gluon colors for an explanation.

The following illustrates the coupling constants for color-charged particles:

The quark colors (red, green, blue) combine to be colorless
The quark anticolors (antired, antigreen, antiblue) also combine to be colorless

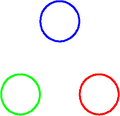A hadron with 3 quarks (red, green, blue) before a color change
Blue quark emits a blue-antigreen gluon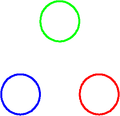
Green quark has absorbed the blue-antigreen gluon and is now blue; color remains conserved
An animation of the interaction inside a neutron. The gluons are represented as circles with the color charge in the center and the anti-color charge on the outside.

Field lines from color charges

Analogous to an electric field and electric charges, the strong force acting between color charges can be depicted using field lines. However, the color field lines do not arc outwards from one charge to another as much, because they are pulled together tightly by gluons (within 1 fm).^[2] This effect confines quarks within hadrons.

Fields due to color charges, as in quarks (G is the gluon field strength tensor). These are "colorless" combinations. Top: Color charge has "ternary neutral states" as well as binary neutrality (analogous to electric charge). Bottom: Quark/antiquark combinations.^[3]^[4]

Coupling constant and charge

In a quantum field theory, a coupling constant and a charge are different but related notions. The coupling constant sets the magnitude of the force of interaction; for example, in quantum electrodynamics, the fine-structure constant is a coupling constant. The charge in a gauge theory has to do with the way a particle transforms under the gauge symmetry; i.e., its representation under the gauge group. For example, the electron has charge −1 and the positron has charge +1, implying that the gauge transformation has opposite effects on them in some sense. Specifically, if a local gauge transformation $ϕ (x)$ is applied in electrodynamics, then one finds (using tensor index notation):

A_{\mu }\to A_{\mu }+\partial _{\mu }\phi (x)

\psi \to \exp[+iQ\phi (x)]\psi

and

\overline \psi \to \exp[-iQ\phi (x)]\overline \psi

where $A_{\mu }$ is the photon field, and $ψ$ is the electron field with $Q = -1$ (a bar over $ψ$ denotes its antiparticle — the positron). Since QCD is a non-abelian theory, the representations, and hence the color charges, are more complicated. They are dealt with in the next section.

Quark and gluon fields and color charges

The pattern of strong charges for the three colors of quark, three antiquarks, and eight gluons (with two of zero charge overlapping).

In QCD the gauge group is the non-abelian group SU(3). The running coupling is usually denoted by α_s. Each flavor of quark belongs to the fundamental representation (3) and contains a triplet of fields together denoted by $ψ$ . The antiquark field belongs to the complex conjugate representation (3^*) and also contains a triplet of fields. We can write

\psi ={\begin{pmatrix}\psi _{1}\\\psi _{2}\\\psi _{3}\end{pmatrix}}

and

\overline \psi ={\begin{pmatrix}{\overline \psi }_{1}^{*}\\{\overline \psi }_{2}^{*}\\{\overline \psi }_{3}^{*}\end{pmatrix}}.

The gluon contains an octet of fields (see gluon field), and belongs to the adjoint representation (8), and can be written using the Gell-Mann matrices as

{{\mathbf A}}_{\mu }=A_{\mu }^{a}\lambda _{a}.

(there is an implied summation over a = 1, 2, ... 8). All other particles belong to the trivial representation (1) of color SU(3). The color charge of each of these fields is fully specified by the representations. Quarks have a color charge of red, green or blue and antiquarks have a color charge of antired, antigreen or antiblue. Gluons have a combination of two color charges (one of red, green or blue and one of antired, antigreen and antiblue) in a superposition of states which are given by the Gell-Mann matrices. All other particles have zero color charge. Mathematically speaking, the color charge of a particle is the value of a certain quadratic Casimir operator in the representation of the particle.

In the simple language introduced previously, the three indices "1", "2" and "3" in the quark triplet above are usually identified with the three colors. The colorful language misses the following point. A gauge transformation in color SU(3) can be written as $ψ \to U ψ$ , where $U$ is a $3 \times 3$ matrix which belongs to the group SU(3). Thus, after gauge transformation, the new colors are linear combinations of the old colors. In short, the simplified language introduced before is not gauge invariant.

Color charge is conserved, but the book-keeping involved in this is more complicated than just adding up the charges, as is done in quantum electrodynamics. One simple way of doing this is to look at the interaction vertex in QCD and replace it by a color-line representation. The meaning is the following. Let $ψ i$ represent the $i$ -th component of a quark field (loosely called the $i$ -th color). The color of a gluon is similarly given by $A$ which corresponds to the particular Gell-Mann matrix it is associated with. This matrix has indices $i$ and $j$ . These are the color labels on the gluon. At the interaction vertex one has $q i \to g i j + q j$ . The color-line representation tracks these indices. Color charge conservation means that the ends of these color-lines must be either in the initial or final state, equivalently, that no lines break in the middle of a diagram.

Since gluons carry color charge, two gluons can also interact. A typical interaction vertex (called the three gluon vertex) for gluons involves g + g → g. This is shown here, along with its color-line representation. The color-line diagrams can be restated in terms of conservation laws of color; however, as noted before, this is not a gauge invariant language. Note that in a typical non-abelian gauge theory the gauge boson carries the charge of the theory, and hence has interactions of this kind; for example, the W boson in the electroweak theory. In the electroweak theory, the W also carries electric charge, and hence interacts with a photon.

References

↑ Feynman, Richard (1985), QED: The Strange Theory of Light and Matter, Princeton University Press, p. 136, ISBN 0-691-08388-6, The idiot physicists, unable to come up with any wonderful Greek words anymore, call this type of polarization by the unfortunate name of 'color,' which has nothing to do with color in the normal sense.
↑ R. Resnick, R. Eisberg (1985), Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.), John Wiley & Sons, p. 684, ISBN 978-0-471-87373-0
↑ Parker, C.B. (1994), McGraw Hill Encyclopaedia of Physics (2nd ed.), Mc Graw Hill, ISBN 0-07-051400-3
↑ M. Mansfield, C. O’Sullivan (2011), Understanding Physics (4th ed.), John Wiley & Sons, ISBN 978-0-47-0746370