Intersecting chords theorem
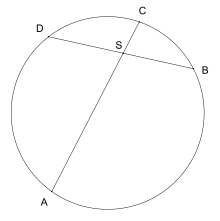
The intersecting chords theorem or just chord theorem is a statement in elementary geometry that describes a relation of the four line segments created by two intersecting chords in a circle. It states that the products of the lengths of the line segments on each chord are equal.
More precisely for two chords AC and BD intersecting in a point S the following equation holds:
The converse is true as well, that is if for two line segments AC and BD intersecting in S the equation above holds, then their four endpoints A, B, C and D lie on a common circle. Or in other words if the diagonals of a quadrilateral ABCD intersect in S and fulfill the equation above then it is a cyclic quadrilateral.
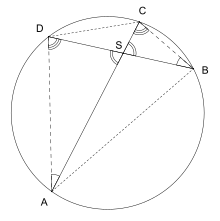
The theorem can be proven using similar triangles. Consider the angles of the triangles ASD and BSC:
This means the triangles ASD and BSC are similar and therefore
Next to the tangent-secant theorem and the intersecting secants theorem the intersecting chord theorem represents one of the three basic cases of a more general theorem about two intersecting lines and a circle - the power of point theorem.
References
- Paul Glaister: Intersecting Chords Theorem: 30 Years on. Mathematics in School, Vol. 36, No. 1 (Jan., 2007), p. 22 (JSTOR)
- Bruce Shawyer: Explorations in Geometry. World scientific, 2010, ISBN 978981310094, p. 14
- Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, p. 149 (German).
- Schülerduden - Mathematik I. Bibliographisches Institut & F.A. Brockhaus, 8. Auflage, Mannheim 2008, ISBN 978-3-411-04208-1, pp. 415-417 (German)
External links
- Intersecting Chords Theorem at cut-the-knot.org
- Intersecting Chords Theorem at proofwiki.org
- Weisstein, Eric Wolfgang. "Chord". MathWorld.