One-key MAC

OMAC (One-key MAC) is a message authentication code constructed from a block cipher much like the CBC-MAC algorithm.

Officially there are two OMAC algorithms (OMAC1 and OMAC2) which are both essentially the same except for a small tweak. OMAC1 is equivalent to CMAC which became an NIST recommendation in May 2005.

It is free for all uses (no patents). In cryptography, CMAC (Cipher-based Message Authentication Code)[1] is a block cipher-based message authentication code algorithm. It may be used to provide assurance of the authenticity and, hence, the integrity of binary data. This mode of operation fixes security deficiencies of CBC-MAC (CBC-MAC is secure only for fixed-length messages).

The core of the CMAC algorithm is a variation of CBC-MAC that Black and Rogaway proposed and analyzed under the name XCBC[2] and submitted to NIST.[3] The XCBC algorithm efficiently addresses the security deficiencies of CBC-MAC, but requires three keys. Iwata and Kurosawa proposed an improvement of XCBC and named the resulting algorithm One-Key CBC-MAC (OMAC) in their papers.[4] They later submitted OMAC1,[5] a refinement of OMAC, and additional security analysis.[6] The OMAC algorithm reduces the amount of key material required for XCBC. CMAC is equivalent to OMAC1.

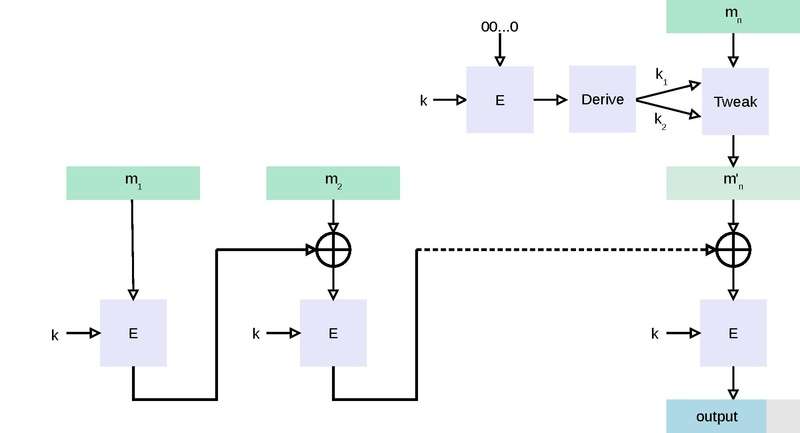
To generate an ℓ-bit CMAC tag (t) of a message (m) using a b-bit block cipher (E) and a secret key (k), one first generates two b-bit sub-keys (k1 and k2) using the following algorithm (this is equivalent to multiplication by x and x2 in a finite field GF(2b)). Let ≪ denote the standard left-shift operator and ⊕ denote exclusive or:

  1. Calculate a temporary value k0 = Ek(0).
  2. If msb(k0) = 0, then k1 = k0 ≪ 1, else k1 = (k0 ≪ 1) ⊕ C; where C is a certain constant that depends only on b. (Specifically, C is the non-leading coefficients of the lexicographically first irreducible degree-b binary polynomial with the minimal number of ones.)
  3. If msb(k1) = 0, then k2 = k1 ≪ 1, else k2 = (k1 ≪ 1) ⊕ C.
  4. Return keys (k1, k2) for the MAC generation process.

As a small example, suppose b = 4, C = 00112, and k0 = Ek(0) = 01012. Then k1 = 10102 and k2 = 0100 ⊕ 0011 = 01112.

The CMAC tag generation process is as follows:

  1. Divide message into b-bit blocks m = m1 ∥ ... ∥ mn−1 ∥ mn where m1, ..., mn−1 are complete blocks. (The empty message is treated as 1 incomplete block.)
  2. If mn is a complete block then mn′ = k1 ⊕ mn else mn′ = k2 ⊕ (mn∥ 10...02).
  3. Let c0 = 00…02.
  4. For i = 1, ..., n-1, calculate ci = Ek(ci−1 ⊕ mi).
  5. cn = Ek(cn−1 ⊕ mn′)
  6. Output t = msbℓ(cn).

The verification process is as follows:

  1. Use the above algorithm to generate the tag.
  2. Check that the generated tag is equal to the received tag.

Implementations

References

  1. ↑ Dworkin, M J. "Recommendation for block cipher modes of operation :" (PDF). doi:10.6028/nist.sp.800-38b.
  2. ↑ Black, John; Rogaway, Phillip (2000-08-20). Advances in Cryptology — CRYPTO 2000. Springer, Berlin, Heidelberg. pp. 197–215. ISBN 3540445986. doi:10.1007/3-540-44598-6_12.
  3. ↑ Black, J; Rogaway, P. "A Suggestion for Handling Arbitrary-Length Messages with the CBC MAC" (PDF).
  4. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003-02-24). "OMAC: One-Key CBC MAC". Fast Software Encryption. Springer, Berlin, Heidelberg. pp. 129–153. doi:10.1007/978-3-540-39887-5_11.
  5. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003). "OMAC: One-Key CBC MAC—Addendum" (PDF).
  6. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003-12-08). "Stronger Security Bounds for OMAC, TMAC, and XCBC". In Johansson, Thomas; Maitra, Subhamoy. Progress in Cryptology - INDOCRYPT 2003. Lecture Notes in Computer Science. Springer Berlin Heidelberg. pp. 402–415. ISBN 9783540206095. doi:10.1007/978-3-540-24582-7_30.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.